1.8. Дуальные цепи.

Дуальные графы. Дуальными называются два графа, если узловая матрица одного из них равна контурной матрице другого (и наоборот):

, (1.23)

. (1.24)

Дуальные элементы схемы. Двухполюсные элементы схемы называются дуальными, если зависимость одного элемента совпадает с зависимостью другого и наоборот.

Источник ЭДС и источник тока дуальны, если . Последнее нужно понимать как численное равенство (ЭДС – в вольтах; ток – в амперах).

Для линейного сопротивления дуальной будет проводимость и наоборот. Действительно, при уравнение совпадает с уравнением . Это совпадение нужно понимать так: если в первом уравнении напряжение (ток) заменить током (напряжением), то получится второе уравнение. Равенство нужно понимать как численное равенство проводимостей (в сименсах) и сопротивлений (в омах).

У дуальных нелинейных резистивных двухполюсников должны совпадать нелинейные зависимости и .

Линейные индуктивные и емкостные двухполюсники характеризуются уравнениями

,

откуда видно, что и - дуальные элементы при .

Равенство нужно понимать как численное равенство индуктивности (в генри) и емкости (в фарадах). В случае нелинейных индуктивных и емкостных двухполюсников дуальность означает совпадение нелинейных характеристик и .

Дуальные схемы. Две схемы электрических цепей, содержащие двухполюсники называются дуальными, если они имеют дуальные графы и каждому элементу одной схемы соответствует дуальный элемент другой.

II. Свойства и методы расчета линейных цепей постоянного тока.

Задача анализа электрической цепи в общем случае состоит в определении токов во всех ветвях цепи. При этом должна быть известна схема цепи, параметры пассивных элементов, а также законы изменения во времени ЭДС и токов источников.

ЭДС источников ЭДС и токи источников тока можно рассматривать как внешние «возмущения», а токи в ветвях цепи как «реакции цепи» на эти возмущения.

Если ЭДС и токи источников постоянны, т.е. не изменяются во времени, то цепи с такими источниками называются цепями постоянного тока. В таких цепях в установившемся режиме токи в ветвях и напряжения на зажимах ветвей также постоянны. Поэтому напряжение на индуктивном элементе равно нулю , равен нулю и ток в емкостном элементе . В связи с этим индуктивный элемент можно заменить коротко замкнутым участком, а емкостный элемент представить в виде ветви с разрывом. Следовательно, токи установившегося режима в ветвях цепи постоянного тока не могут зависеть от и , эти токи определяются только резистивными элементами, т.е. параметрами и .

Рассмотрим методы расчета линейных цепей постоянного тока в установившемся режиме.

2.1. Расчет простых цепей постоянного тока.

а ) Расчет при последовательном соединении участков цепи.

П

Рис.2.1

ри последовательном соединении участков цепи (рис. 2.1) напряжение на зажимах всей цепи равно сумме напряжений на отдельных участках цепи.

,

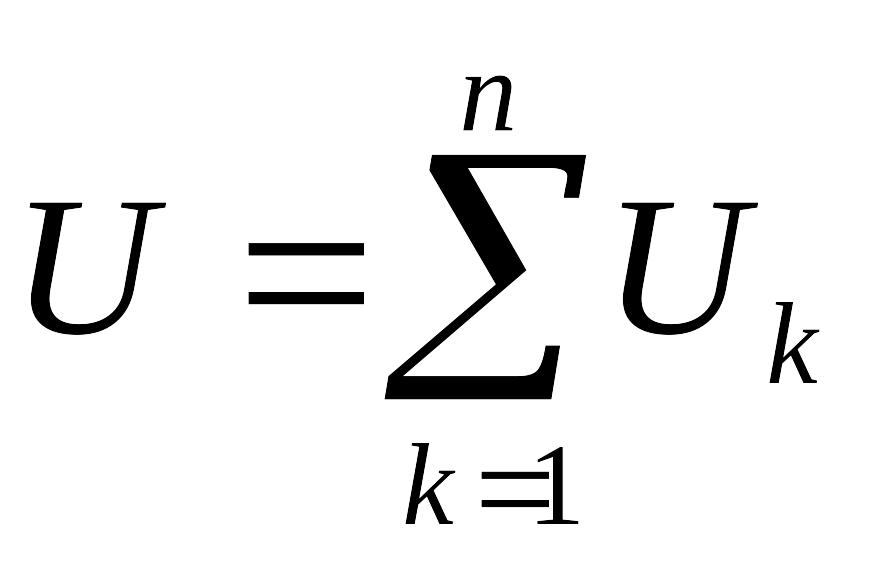т. к. , то

, .

Таким образом, при последовательном соединении сопротивление всей цепи равно сумме сопротивлений отдельных участков.

Мощность, поступающая в цепь

.

б ) Расчет при параллельном соединении участков цепи.

П

Рис. 33

ри параллельном соединении участков цепи (ветвей) ток на входе цепи равен сумме токов в отдельных участках (ветвях) (рис. 2.2)

.

Но , поэтому

, .

Таким образом, при параллельном соединении участков проводимость всей цепи равна сумме проводимостей отдельных участков цепи (ветвей).

Мощность, поступающая в цепь

.

в) Расчет при смешанном соединении участков цепи (рис. 2.3).

Под смешанным соединением понимается соединение, представляющее сочетание последовательных и параллельных соединений участков цепи. Для расчета таких цепей можно использовать методы, рассмотренные в п.п. а) и б).

Ветви 2 и 3 соединены параллельно. Складывая проводимости этих ветвей, получаем проводимость ветви, эквивалентной указанным двум ветвям

.

При этом исходная схема преобразуется в схему из двух последовательно соединенных участков с сопротивлениями и (рис. 2.4)

.

Возвращаясь к исходной схеме, получаем

,

или

, .