1.6. Граф электрической цепи.

Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Рассмотрим соотношения в электрической цепи, обусловленные способом соединения элементов.

Пусть цепь состоит из двухполюсников. В простейшем случае эти элементы могут быть соединены последовательно или параллельно.

При последовательном соединении любые два соседних элемента имеют общий зажим (рис. 1.28), токи во всех элементах одинаковы. Напряжение на зажимах всего соединения равно сумме напряжений отдельных элементов

. (1.13)

При параллельном соединении все элементы присоединяются к одной и той же паре узлов, так что напряжения на всех элементах одинаковы (рис. 1.29). Ток в неразветвленной части цепи равен сумме токов всех элементов

. (1.14)

Соотношения (1.13) и (1.14) справедливы для соединений любых элементов (резистивных, индуктивных и т. д.). Их вид определяются только способом соединения элементов, или, как говорят, геометрией (топологией) соединений.

Т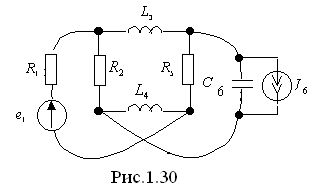 опологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому каждую ветвь можно изобразить отрезком прямой. На рис. 1.31 показан граф электрической цепи, изображенной на рис. 1.30.

Н а графе источники ЭДС и тока не изображаются. При этом ветвь с источником ЭДС сохраняется, ветвь с источником тока не показывается. Отрезки прямых называются ветвями графа, концевые точки ветви графа – узлами графа.

Ветвям графа может быть дана определенная ориентация, указанная стрелками. Граф, у которого все ветви ориентированы, называется ориентированным. В противном случае - неориентированным.

Подграфом графа называется часть графа (одна ветвь, один узел, любое множество ветвей и узлов графа). В теории цепей различают подграфы: путь, контур, дерево, связи и сечение.

Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел в этом пути встречается один раз. На рис. 1.31 имеем пути: 3-4-5; 2-1-5 и т.д.

Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. На рис. 1.31 имеем контуры: 2-3-6, 2-3-5-4 и т.д.

Если между любой парой узлов графа (схемы) существует путь, то такой граф (схема) называется связным.

Деревом связного графа (схемы) называют связной подграф (подсхему), содержащий все узлы графа (схемы), но ни одного контура. Деревья графа рис. (1.31) показаны на рис. 1.32.

Ветви графа (схемы), которые дополняют дерево до исходного графа, называются ветвями связи (дополнениями дерева). Ветви связи деревьев рис. 1.32 показаны на рис. 1.33.

Если граф (схема) содержит « » ветвей и « » узлов, то число ветвей любого дерева . Число ветвей связи графа .

С ечением графа (схемы) называется множество ветвей, удаление которых делит граф (схему) на два изолированных подграфа (подсхемы), один из которых в частном случае может быть изолированным узлом. Сечение можно изобразить в виде следа замкнутой поверхности, рассекающей соответствующие ветви. Такие поверхности ( ; ) показаны на рис. 1.34.

Г лавным контуром называется контур, состоящий из ветвей дерева и только одной ветви связи. Число главных контуров .

Главным сечением называется сечение, состоящее из ветвей связи и одной ветви дерева. Каждая ветвь дерева позволяет образовать одно главное сечение. Число главных сечений .

На рис. 1.35 жирными линиями показано дерево. Главные контуры: 2-3-6; 3-5-1; 2-3-5-4. Главные сечения: изображены поверхностями ; и .

Вопрос о числе независимых уравнений, которые можно составить по законам Кирхгофа, можно решить, применяя понятие дерева графа (схемы). Можно показать, что:

• уравнения по I закону Кирхгофа, составленные для главных сечений – независимы;

• уравнения по II закону Кирхгофа для главных контуров – независимы.

По I закону Кирхгофа составляют независимых уравнений. По II закону Кирхгофа составляют независимых уравнений.