1.5. Основные уравнения цепей с сосредоточенными параметрами.
Эти уравнения вытекают из известных физических законов – принципа непрерывности полного тока и закона электромагнитной индукции.
Если
некоторый узел схемы охватить замкнутой
поверхностью
(рис. 1.25), то в силу принципа непрерывности
полного тока
,
(1.6)
где
-
плотность полного тока, то есть суммы
тока проводимости и тока смещения. В
схеме с сосредоточенными параметрами
ток смещения существует только между
электродами емкостей, поэтому в (1.6)
плотность полного тока равна плотности
тока проводимости:
.
отличен от нуля в тех точках поверхности
,
которые совпадают с поперечным сечением
проводников. Учитывая это из (1.6) получим
.
(1.8)
У
равнение
(1.8) называется первым законом Кирхгофа:
алгебраическая
сумма токов ветвей, соединенных в узле,
равна нулю в любой момент времени.
При этом положительные значения
присваивают токам, направленным от узла
или из замкнутой поверхности
.
Первый закон Кирхгофа справедлив и для замкнутой поверхности, охватывающей несколько узлов. При этом в (1.7) суммируются токи ветвей, рассекаемых поверхностью. (1.7) можно записать в виде
,
(1.8)
где
- алгебраическая сумма токов источников
тока;
-
алгебраическая сумма токов других
ветвей (элементов). В (1.8) положительный
знак присваивают
,
направленному к узлу;
,
направленному от узла.
По закону электромагнитной индукции для любого замкнутого контура имеем
.
(1.9)
Направление интегрирования и направление потока согласованы по правилу правого винта.
Возьмем замкнутый контур на схеме цепи, так чтобы он проходил вне источников и индуктивностей. Так как в цепи с сосредоточенными параметрами магнитное поле сосредоточенно в индуктивности, то для указанного контура (1.9) дает
,
(1.10)
т.е. поле вектора потенциально и напряжение между любыми двумя точками контура совпадает с разностью потенциалов. Из (1.10) следует
.
(1.11)
Э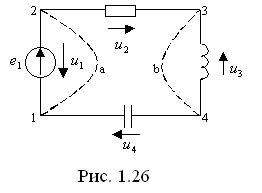
то
уравнение называют вторым законом
Кирхгофа: алгебраическая
сумма напряжений ветвей (элементов)
контура равна нулю в любой момент
времени. С
положительным знаком берется напряжение,
положительное направление которого
совпадает с направлением обхода контура.
Рассмотрим схему, приведенную на рис. 1.26. Берем замкнутый контур 1а23б41.
Для этого контура (1.11) имеет вид
,
,
,
,
.
Если в (1.11) напряжения источников перенести в правую часть и заменить их ЭДС, то
,
(1.12)
т.е.
алгебраическая сумма напряжений на
пассивных элементах
равна алгебраической сумме ЭДС контура
.
В (1.12) с положительным знаком записывают
напряжения и ЭДС, направления которых
совпадают с направлением обхода контура.
Пример. Составить уравнения Кирхгофа для схемы, показанной на рис. 1.27.
Д
ля
узла 1:
.
Для
контура
при обходе по часовой стрелке:
Рис.1.27
.
Для
контура
при обходе по часовой стрелке можно
записать
.