1.4. Двухполюсные пассивные элементы.

Основными двухполюсными пассивными элементами схемы являются резистивный (сопротивление или проводимость), индуктивный и емкостный элементы.

Резистивный элемент. Двухполюсный элемент, характеризуемый зависимостью или , называется резистивным элементом, а сама зависимость или вольтамперной характеристикой (ВАХ). На рис. 1.13 показана нелинейная ВАХ (она характерна для полупроводникового диода), а на рис. 1.14 линейная ВАХ.

С опротивление (проводимость), соответствующее рис. 1.13, зависит от тока (напряжения) и называется нелинейным; сопротивление (проводимость), соответствующее рис. 1.14, от тока (напряжения) не зависит и называется линейным (оно постоянно). Обозначение такого сопротивления дано на рис. 1.15. В этом случае имеет место соотношение (закон Ома):

(1.3)

где R - сопротивление; проводимость.

Сопротивление - пассивный элемент. Энергия, поступающая в него

.

Эта энергия преобразуется в тепло. При этом мощность этого преобразования определяется уравнением (закон Джоуля-Ленца).

С опротивление как элемент схемы соответствует элементу цепи – резистору. Примером резистора может служить проводящий цилиндр (рис. 1.16).

Напряжение между точкам 1 и 2 равно

,

ток равен

.

Если ток распределен равномерно по сечению ( ), а напряженность одинакова по длине, то

, .

По закону Ома в дифференциальной форме

; .

Поэтому

.

П ри переменном токе сопротивление цилиндра увеличивается за счет неравномерного распределения тока из-за поверхностного эффекта и эффекта близости (о них будет сказано далее).

Индуктивный элемент. Двухполюсник, характеризуемый зависимостью или , называется индуктивным элементом, а зависимость называется вебер-амперной характеристикой. - потокосцепление измеряется в веберах (Вб). На рис. 1.17 дана нелинейная ВАХ, а на рис. 1.18 – линейная ВАХ.

У линейного индуктивного элемента (рис.1.18)

, ,

L – индуктивность, измеряется в генри (Г). Обозначение линейной индуктивности ( ) дано на рис. 1.19.

Напряжение на зажимах индуктивности равно

.

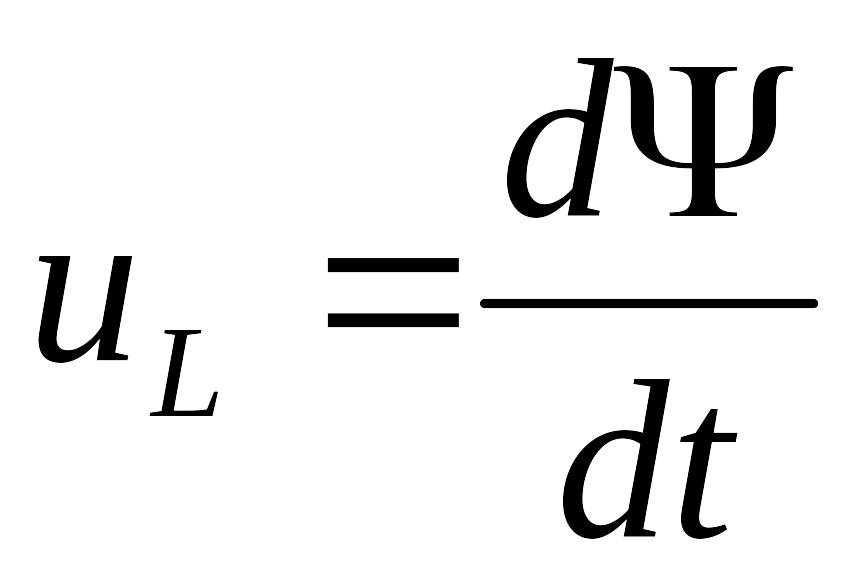
В случае линейной индуктивности

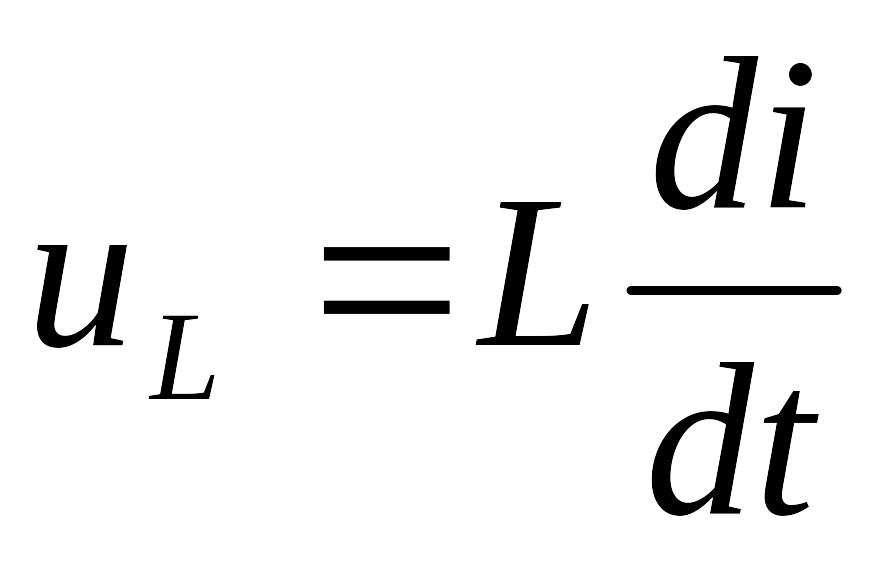, . (1.4)

Индуктивность как схемный элемент соответствует элементу цепи – индуктивной катушке.

Индуктивную катушку можно представить в виде кольцевого сердечника, на который равномерно намотана обмотка (рис. 1.20). Ток в обмотке создает магнитный поток , замыкающийся в сердечнике (потоком рассеяния, который частично замыкается по воздуху, пренебрегаем). Направления и связаны правилом правого винта. Потокосцепление катушки , где - число витков обмотки. Магнитный поток равен

,

где - магнитная индукция, , - магнитная постоянная. По закону полного тока имеем

.

Если существенно больше поперечных размеров сердечника, то поток можно считать равномерно распределенным по сечению сердечника и, следовательно,

, .

Тогда

.

Из (1.4) видно, что отлично от нуля только при ( ). Изменяющийся ток создает изменяющийся магнитный поток и по закону электромагнитной индукции в обмотке индуцируется ЭДС, называемая ЭДС самоиндукции.

или при

.

Линейная индуктивность ( ) – пассивный элемент. Энергия, поступающая в такой элемент, равна

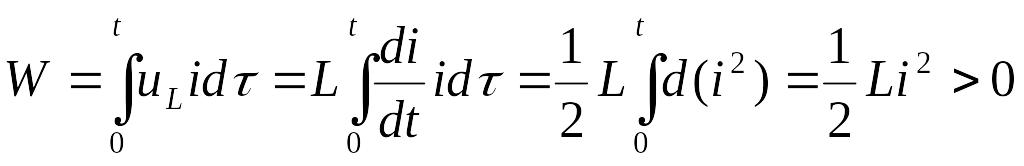
при условии . Эта энергия запасается в магнитном поле катушки.

Емкостный элемент. Если двухполюсник характеризуется зависимостью или , то его называют емкостным элементом (емкостью), а указанные зависимости кулон-вольтной характеристикой. Здесь - электрический заряд, так что

.

На рис. 1.21 и 1.22 соответственно показаны характеристики для нелинейной и линейной емкостей.

У линейного емкостного элемента

,

где 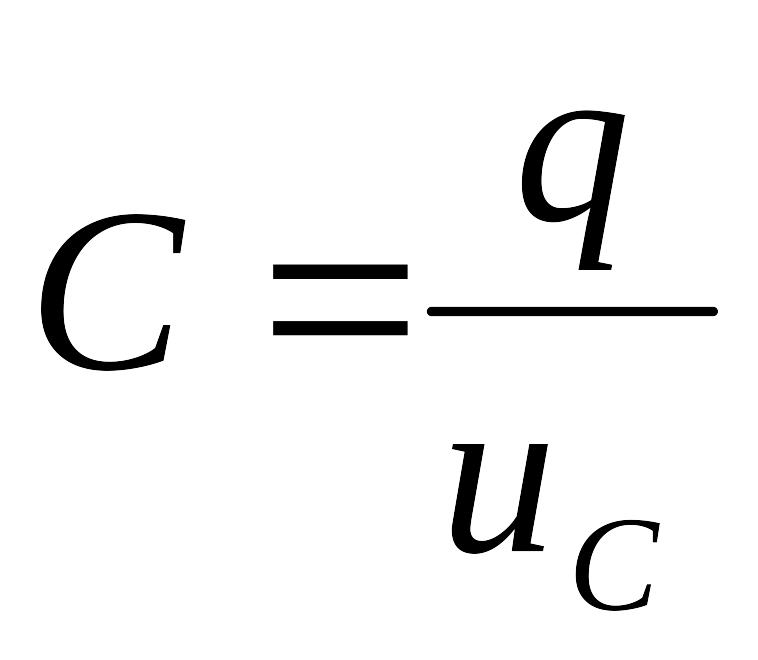- емкость, измеряется в фарадах (Ф). Обозначение линейной емкости дано на рис. 1.23.

Ток через емкость .

Если , то

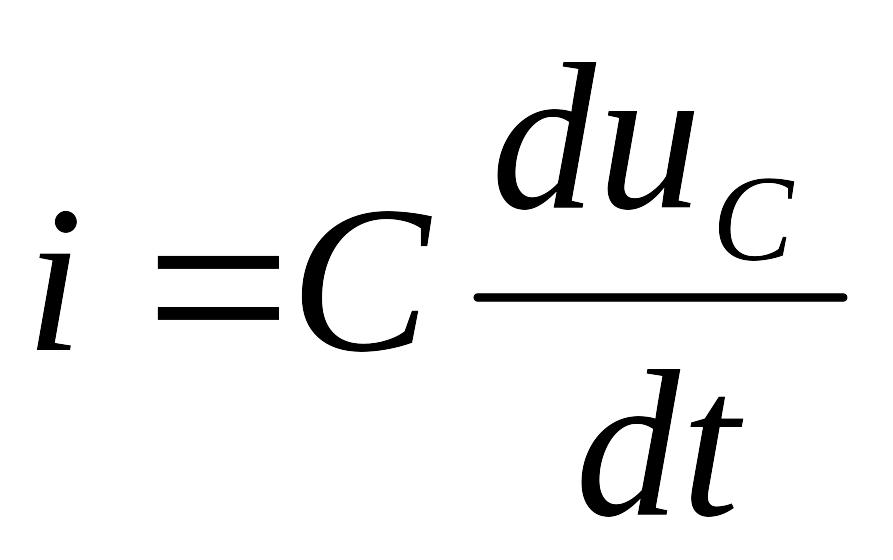, . (1.5)

Емкость как схемный элемент соответствует элементу цепи – конденсатору.

Конденсатор можно представить в виде двух параллельных проводящих пластин площадью S, разделенных диэлектриком толщиной (рис. 1.24).

При на левом электроде будет заряд , на правом - .

, ,

- электрическая постоянная.

Если поле в конденсаторе однородно, то

и емкость будет равна

.

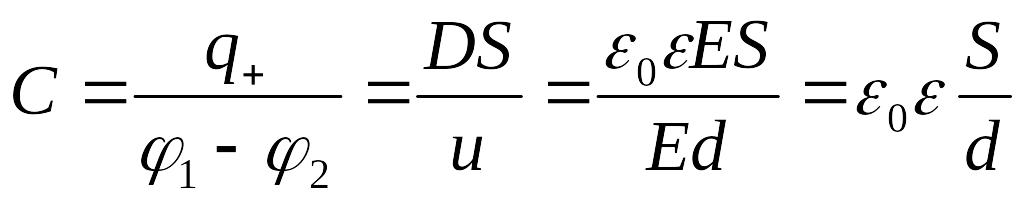Как видно из (1.5) ток через емкость отличен от нуля только при . Изменение напряжения на электродах вызывает изменение величины заряда на электродах.

Линейная емкость ( ) представляет собой пассивный элемент. Энергия, поступающая в него, равна

при . В данном случае энергия запасается в электрическом поле.

Процесс запасания энергии, как в магнитном, так и в электрическом поле является обратимым. Запасенная энергия может быть отдана другим элементам (например, разряд конденсатора на сопротивление).

Схемы замещения резисторов, индуктивных катушек и конденсаторов.

	схема резистора
	схема индуктивной катушки
	схема конденсатора

Схемные элементы – сопротивление , индуктивность , емкость - отражают основные свойства и параметры соответственно резисторов, индуктивных катушек и конденсаторов, обусловленные физическими процессами необратимого рассеяния энергии и обратимого накопления энергии, связанного с магнитным и электрическим полями. С помощью схемных элементов , и можно составить схемы замещения резисторов, индуктивных катушек и конденсаторов, учитывающие и побочные процессы.