2.7. Принцип (свойство) взаимности.

Пусть в схеме цепи все источники электрической энергии представлены в виде источников ЭДС. Тогда согласно (2.32) имеем

.

Рассмотрим два режима работы цепи, отличающиеся только значениями ЭДС. Для первого режима

, .

Для второго режима

, .

Запишем соотношения

,

.

Левые части равенств при транспозиции не изменяются, поэтому

.

Т. к. матрица симметрична, то . Поэтому

(2.37)

или

, (2.38)

Формулы (2.37) и (2.38) выражают в общем виде принцип взаимности электрических цепей. Согласно этому принципу, сумма произведений ЭДС ветвей первого режима на токи ветвей второго режима равна сумме произведений ЭДС второго режима на токи первого.

Если в схеме цепи все источники энергии представлены как источники тока, то согласно (2.36)

.

В этом случае аналогично предыдущему справедливы равенства

(2.39)

или

, (2.40)

где

,

- матрицы токов источников тока первого и второго режимов.

, - матрицы напряжений ветвей первого и второго режимов.

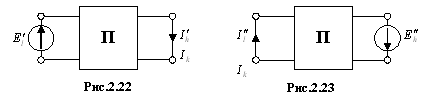
(2.38) и (2.40) – общие выражения принципа взаимности. Из них следуют частные случаи.

Рис. 2.22 соответствует первому режиму. В этом режиме в цепи имеется только один источник ЭДС, который в ветви создает ток . П – имитирует пассивную часть рассматриваемой цепи.

Рис. 2.23 соответствует второму режиму.

Поскольку матрицы и имеют по одному элементу и , то из (2.38) имеем

.

Если , то .

Если в цепи имеется один источник тока (рис.2. 24, рис. 2.25), то из (2.40) имеем

.

При получим .

Р авенства (2.37) – (2.40), служащие общими определениями взаимности, вытекают из условия симметрии матриц входных и взаимных проводимостей и сопротивлений и . Симметрия этих матриц, в свою очередь, установлена из условий симметрии матриц узловых проводимостей и контурных сопротивлений . Таким образом, симметрию матриц и , и рассматривают как признак цепей, удовлетворяющих принципу взаимности.

2.8. Теорема о компенсации.

Любое сопротивление (рис. 2.26) с током можно заменить источником ЭДС , направление которой противоположно направлению тока (или источником ЭДС , направление которой совпадает с направлением тока). При этом токи и

напряжения всех ветвей не изменяются. В общем случае любую ветвь с напряжением на ее зажимах можно заменить источником ЭДС . Кроме того, любую ветвь с током можно заменить источником тока , направление которого совпадает с направлением тока ветви (источником тока , направление которого противоположно направлению тока ветви) без изменения токов и напряжений всех ветвей схемы.

Указанные положения о возможности замены ветвей источниками ЭДС и тока определяют теорему о компенсации.

2.9. Теорема об эквивалентном источнике.

Рис.2.28 Рис.2.29

Пусть в схеме электрической цепи, имеющей источники ЭДС и тока, выделена –я ветвь, содержащая только сопротивление с током (рис.2.28).

Если сопротивление заменить согласно теореме о компенсации источником тока (рис.2.29), направление которого противоположно направлению тока , то напряжение на зажимах ветви можно записать в виде

,

где – слагаемое, объединяющее напряжения на ветви, обусловленное всеми источниками, кроме .

,

где – входное сопротивление относительно зажимов выделенной ветви ( ). Это сопротивление определяется при условии, что в схеме исключены все источники, кроме . подставляет напряжение при , то есть напряжение на зажимах разомкнутой –й ветви. Учитывая, что , и опуская индекс , напряжение на зажимах выделенной ветви можно записать

. (2.41)

На рис. 2.30 показана схема, в которой выделена ветвь с сопротивлением .

Напряжение на зажимах ветви равно . Поэтому из (2.41) следует

. (2.42)

Выражению (2.42) соответствует эквивалентная схема на рис. 2.31. В этой схеме ЭДС равна напряжению на зажимах разомкнутой ветви с сопротивлением .

Если цепь с сопротивлением короткозамкнута, то и сопротивление , где – ток в короткозамкнутой выделенной ветви.

Считая внутренним сопротивлением источника напряжения (рис. 2.31) и заменяя его источником тока, получим схему (рис 2.32), в которой ток источником тока равен . Для этой схемы

, (2.43)

где ,

. (2.444)

Формулы (2.42) и (2.43) определяют теорему об эквивалентном источнике или об эквивалентном двухполюснике: если активный двухполюсник, к которому присоединена некоторая пассивная ветвь, заменить источником ЭДС с ЭДС, равным напряжению на зажимах разомкнутой ветви (источником тока, величина которого равна току короткого замыкания ветви), и сопротивлением, равным входному сопротивлению активного двухполюсника (проводимостью, равной проводимости активного двухполюсника), то ток в этой ветви (напряжение на ее зажимах) не изменится. Эквивалентную схему с источником ЭДС (рис. 2.31) называют схемой Тевенена, а эквивалентную схему с источником тока (рис. 2.32) называют схемой Нортона.

В общем случае выделенная ветвь может содержать источник ЭДС . Тогда, вместо (2.42),

, (2.45)

где знак плюс соответствует случаю, когда направление ЭДС совпадает с направлением тока, а знак минус – когда направление ЭДС противоположно

направлению тока. Если ветвь содержит источник тока , то

. (2.46)

Согласно теореме об активном двухполюснике, реальный режим работы выделенной ветви может быть рассчитан как наложение двух режимов: первого режима, при котором выделенная ветвь разомкнута, ток , напряжение на зажимах ветви от действующих источников активного двухполюсника равно (выделенная ветвь короткозамкнута, напряжение , ток ), и второго режима, при котором в схеме действует один источник ЭДС (источник тока ). Ток (напряжение ) выделенной ветви равен току ( напряжению) этой ветви во втором режиме.

Для нескольких выделенных ветвей вместо (2.41) и (2.44) имеем

, (2.47)

, (2.48)

где , – матрица напряжений, токов выделенных ветвей; , – матрица напряжений на зажимах разомкнутых выделенных ветвей, токов короткозамкнутых выделенных ветвей; , – матрица входных и взаимных сопротивлений (проводимостей) выделенных ветвей.

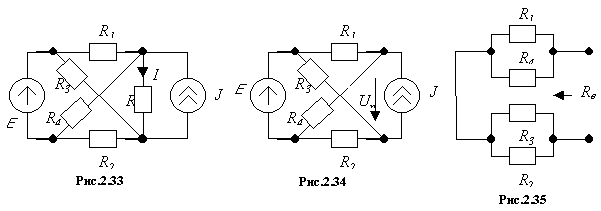
Пример

Определим ток (рис. 2.33) с помощью теоремы об эквивалентном источнике. При размыкании ветви с сопротивлением , получим схему, изображенную на рис. 2.34.

Напряжение на разомкнутой ветви равно

.

По схеме на рис. 2.35 находим

.

Искомый ток равен

.

ЛИТЕРАТУРА

Основная

1. Нейман Л.Р., Демирчян К.С. ТОЭ. - Л.: Энергоиздат, 1981. - Т. 1,2.

2. Теоретические основы электротехники. Под ред. П.А. Ионкина. Т. 1,2. - М.: ВШ., 1976.

3. Теоретические основы электротехники. Под ред. Г.И. Атабекова. Т. 1,2 - М.: Энергия, 1979.

4. Сборник задач и упражнений по ТОЭ. Под ред. П.А. Ионкина. - М.: Энергоиздат, 1982. - 766с.

5. Пашенцев И.Д. Методические пособия по решению задач курса ТОЭ. - Л.: ЛИИЖТ, 1981. - Ч. I-VI.

6. Бессонов Л.А. Сборник задач по ТОЭ. - М.: ВШ, 1988.

7. Бессонов Л.А. Теоретические основы электротехники. - М.: ВШ, 1978. - Т.1,2.

8. Новгородцев А.Б. 30 лекций по теории электрических цепей. - СПб.: Политехника, 1995. - 519с.

9. Шимони К. Теоретическая электротехника. - М.: МИР, 1964. - .773с.

10. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. - М.: Энергоиздат, 1989. - 333с.

11. Белецкий А.Ф. Теория линейных электрических цепей. - М.: Радио и связь, 1986. - 554с.

12. Поливанов К.М. Теоретические основы электротехники. - М.: Энергия, 1975. - Т.3. - 352с.

13. Литература информационно-методического обеспечения учебного процесса, разработанная кафедрой ТОЭ.

Дополнительная

1. Матханов П.Н. Основы анализа электрических цепей. - М.: ВШ, 1990

2. Практикум по ТОЭ. Под ред. Шакирова М.А. - СПб.: СПбГТУ, 1995. - Ч. 1,2,3

3. Шебес М.Р. Задачник про теории линейных электрических цепей. - М.:ВШ, 1973. - 655с.

4. Демирчян К.С., Бутырин П.Л. Моделирование и машинный расчет электрических цепей. - М.: ВШ, 1988.

5. Кухаркин Е.С. Основы технической электродинамики. - М.: ВШ, 1969 - Ч. 1,2.

Рекомендуется использование программ, сочетающих в себе необходимость понимания физических явлений при постановке задачи исследования электромагнитных процессов и минимальности затрат времени на реализацию ее решения на компьютере, включая использования пакетов программ Pspice, Workbench, Matlab, Mathcad, Elcut.

60