2.4. Расчет сложных цепей постоянного тока методом контурных уравнений.

В качестве искомых величин можно принять токи ветвей связи, или так называемые контурные токи. Знание контурных токов позволяет найти все реальные токи в схеме.

Уравнения с контурными токами (контурные уравнения) получают на основе второго закона Кирхгофа; их число равно числу независимых уравнений, составленных для контуров, т.е. .

Закон Ома в матричной форме, как известно, имеет вид

.

Умножим обе части равенства на матрицу и учтем . Тогда

. (2.18)

Токи в ветвях через контурные токи определяются по формуле

. (2.19)

Контурные уравнения в матричной форме получаем, подставляя (2.19) в (2.18)

. (2.20)

Если обозначить

, ,

,

то (2.20) получает вид

, (2.11)

где - матрица контурных сопротивлений, - матрица контурных ЭДС. В развернутой форме уравнение (2.21) выглядит следующим образом

. (2.22)

При большом числе независимых контуров уравнение (2.22) решается с помощью компьютера приближенно. При малом уравнение (2.22) можно решить аналитически.

З аписываем (2.22) в виде системы алгебраических уравнений

отсюда

,

- главный определитель системы, - алгебраическое дополнение.

Пример

Рассмотрим цепь, показанную на рис. 2.15. Схема цепи имеет четыре узла и шесть ветвей. Число независимых контуров , контуры обхода показаны стрелками и римскими цифрами. Граф с выбранным деревом (ветви 1, 2, 3) также показан на рис. 2.16.

Матрица контуров равна

.

Диагональная матрица сопротивлений ветвей

.

Матрица контурных сопротивлений

.

Матрица ЭДС источников ЭДС ветвей

.

Матрица токов источников тока ветвей

.

Матрица контурных ЭДС

.

Матрица контурных токов

.

Таким образом, контурные уравнения имеют вид

,

где ; ; ; ; ; ; ; ; .

В этом примере контурные токи , , совпадают с токами 4, 5, 6, т.е. с токами ветвей связи (рис. 2.16).

Токи в других ветвях находим по схеме, зная контурные токи

, , .

Выводы:

• Матрица контурных сопротивлений квадратная порядка . Диагональные элементы матрицы называются собственными контурными сопротивлениями, собственное контурное сопротивление равно сумме сопротивлений ветвей соответствующего контура с положительным знаком. Недиагональные элементы 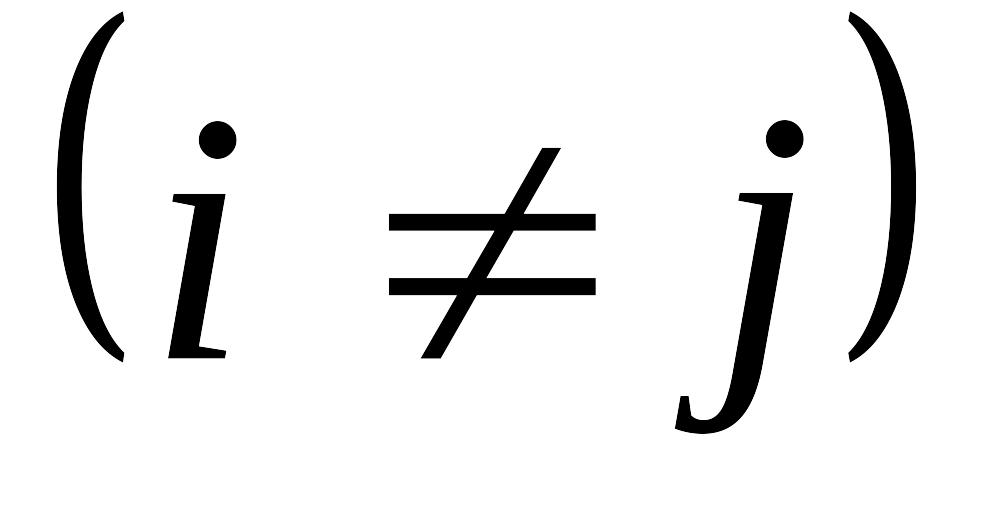называются общими контурными сопротивлениями. Общее контурное сопротивление равно сопротивлению ветви, общей для контуров и , и записывается с положительным знаком, если контурные ток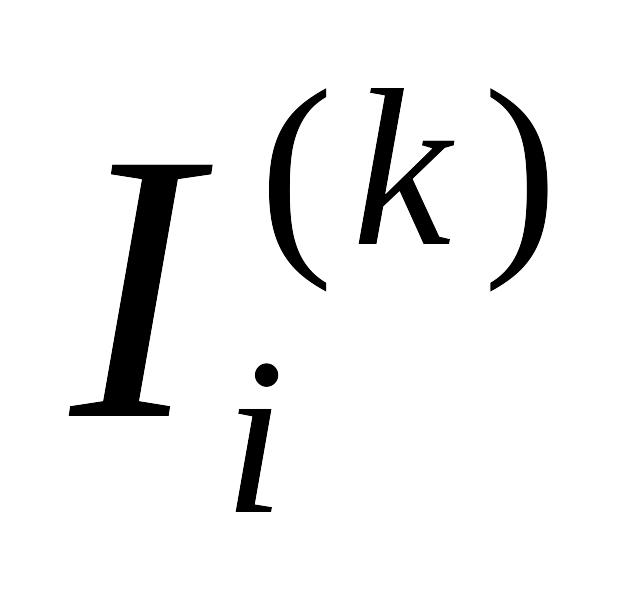и и 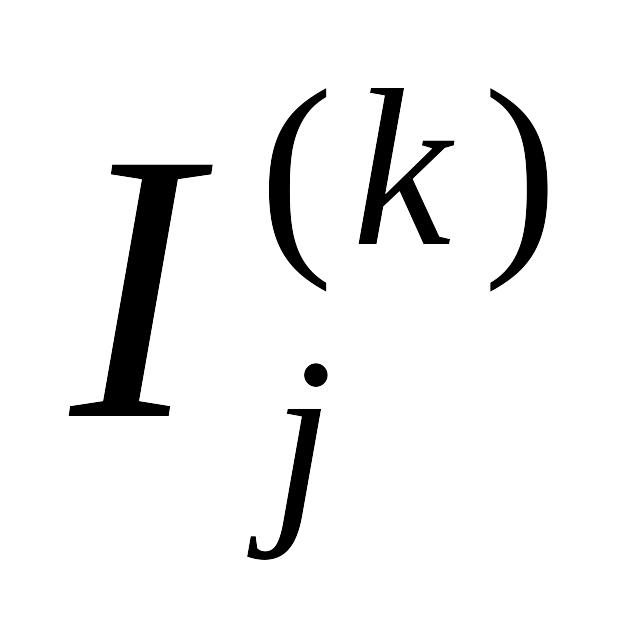в общей ветви направлены одинаково.

• Матрица симметрична, т.е. , .

• Элемент 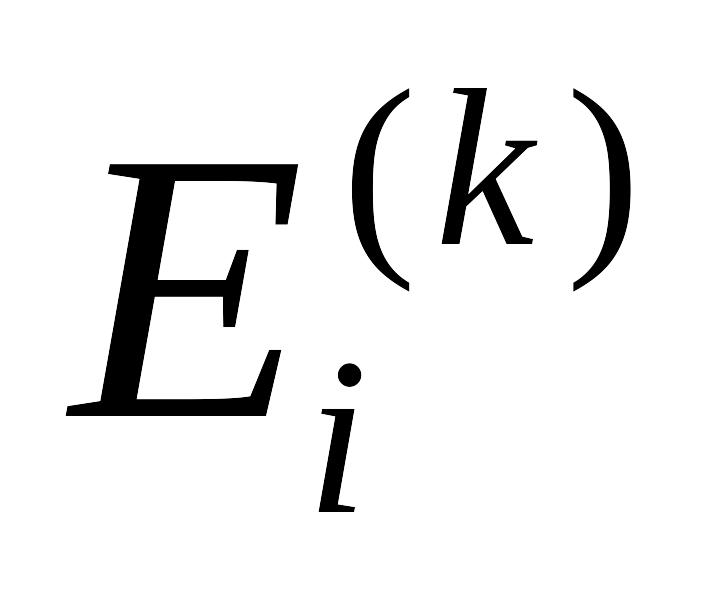матрицы контурных ЭДС равен алгебраической сумме ЭДС источников ЭДС -го контура, включая ЭДС источников, эквивалентных источникам тока. При этом с положительным знаком записывают ЭДС, направление которых совпадают с направлением обхода контура. Следовательно, контурные уравнения можно составить непосредственно из рассмотрения схемы.

Если в схеме имеются ветви с идеальными источниками тока, то сопротивление таких ветвей . В этом случае для записи уравнения (2.20) необходимо использовать преобразование, описанное выше. Ветви с идеальными источниками ЭДС преобразования не требуют, в матрице таким ветвям соответствуют элементы .

Пример.

Рассмотрим цепь, приведенную на рис. 2.17. Схема цепи имеет три узла и четыре ветви. Число независимых контуров . Направление обхода контуров выбираем по часовой стрелке (рис. 2.18).

Матрица контуров

.

Диагональная матрица ветвей

.

Матрица контурных сопротивлений

.

Таким образом, , , .

Матрица ЭДС источников ЭДС

.

Матрица токов источников тока

.

Матрица контурных ЭДС

,

, .