4.4. Основные свойства и преобразование цепей синусоидального тока.
Основные свойства.
В цепи, содержащей источники синусоидальных ЭДС и токов, для мгновенных мощностей ветвей выполняется соотношение
.
(4.13)
Кроме того, справедливо соотношение
,
(4.14)
.
(4.15)
где
ток сопротивления
(рис. 4.6)
Соотношение (4.14) – математическая формулировка баланса комплексных мощностей. В правой части равенства (4.15) записана сумма комплексных мощностей, генерируемых источниками ЭДС и тока.
.
Подставляя
в левую часть (4.15)
,получим
,
.
Таким образом, в
цепи с синусоидальными ЭДС и токами
выполняется баланс активной и реактивной
мощностей: активная мощность, генерируемая
источниками равна активной мощности,
рассеиваемой в сопротивлениях
;
реактивная мощность источников равна
реактивной мощности в реактивных
сопротивлениях
(реактивную мощность индуктивного
сопротивления учитываем с положительным
знаком, а емкостного – с отрицательным). Принцип
наложения, свойство взаимности, теорема
о компенсации и об эквивалентном
источнике справедливы и для цепей
синусоидального тока. Математические
соотношения цепей синусоидального
тока, записанные в комплексной форме
аналогичны соответствующим соотношениям
цепей постоянного тока.
Методы преобразования цепей.
Все методы преобразования цепей постоянного тока применимы и к цепям с синусоидальными ЭДС и токами.
В результате преобразования цепей с источниками тока могут появиться ветви с отрицательным активным сопротивлением.
5. Индуктивно-связанные цепи
5 .1. Эдс самоиндукции и взаимоиндукции
П
усть
имеется катушка с током
(рис. 5.1).
Образуется магнитное поле. Это поле
можно представить в виде магнитных
линий, сцепленных с витками катушки.
Магнитные
линии представляют магнитный поток
,
сцепленный со всеми витками, а магнитные
линии, соответствуют потоку
,
сцепленному
с частью витков. Вычислим потокосцепление
катушки. Под потокосцеплением понимается
произведение потока на число витков, с
которыми этот поток сцепляется.
Потокосцепление катушки, обусловленное
током этой же катушки, называется
потокосцеплением самоиндукции и
обозначается
[Вебер=В·сек].
В рассматриваемом случае
.
В общем случае
,
где – собственная индуктивность или просто индуктивность [Генри=Ом·cек].
Если ток переменный, то изменяется во времени и потокосцепление, и в катушке индуктируется ЭДС самоиндукции, которая равна
.
При
.
Напряжение самоиндукции на катушке равно
.
Пусть
,
тогда
,
,
следовательно
.
(5.1)
Рассмотрим
случай двух катушек (рис. 5.2). Пусть ток
имеется только в первой катушке. Магнитное
поле, создаваемое этим током, состоит
из двух частей.
сцепляется только с первой катушкой,
с обоими катушками. Поток
,
сцепляющийся со второй катушкой, но
создаваемый током первой катушки,
называется потоком взаимной индукции.
Потокосцепление взаимной индукции
обозначим
.
Можно записать
,
–
взаимная индуктивность
[Генри=Ом·cек].
Если изменится ток
,
то во второй катушке индуктируется ЭДС
взаимной индукции.
.
При
.
Напряжение, необходимое для преодоления этой ЭДС равно
.
Если
,то
для комплексных действующих значений
получаем
. (5.2)
Допустим
теперь, что ток имеется только во второй
катушке. Тогда потокосцепление взаимной
индукции первой катушки, обусловленное
током
второй катушки, будет равно
.
Для ЭДС взаимной
индукции, индуктируемой в первой катушке,
получим при
,
.
Полагая , то для комплексных действующих значений получим
. (5.3)
Коэффициенты
взаимной индукции
и
определяются
геометрией катушек и тем, как они
расположены друг относительно друга.
Поэтому эти величины должны быть
одинаковыми, то есть
.
(5.4)
Этот
факт называется принципом взаимности.
В связи с этим далее коэффициенты
взаимной индукции будем обозначать
.
Для всякого электрического контура
всегда
.
Взаимная индуктивность может быть как
положительной, так и отрицательной в
зависимости от направлений токов в
катушках. Если эти токи направлены таким
образом, что направления потоков
(потокосцеплений) самоиндукции и взаимной
индукции совпадают (согласное включение),
то надо считать
.
Если поток взаимной индукции направлен
встречно потоку самоиндукции, то надо
считать
.
Для того, чтобы при расчетах была определенность, один из зажимов катушек снабжают маркировкой (* или ●).
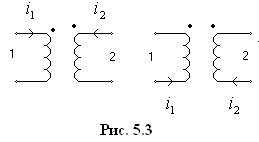Маркировку
производят таким образом, чтобы при
одном и том же направлении токов в
катушке: либо от маркированного зажима
к другому, либо напротив взаимная
индуктивность была положительной (рис.
5.3).
Рассмотрим теперь два случая (рис. 5.4 и рис. 5.5).
Направление ЭДС и напряжения взаимной индукции относительно маркировки в данной катушке такое же, что и направление обеспечивающего их тока относительно маркировки другой катушки.
Н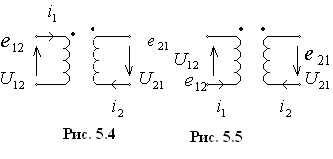
аправление
ЭДС и напряжения самоиндукции не зависит
от маркировки и всегда совпадает с
направлением соответствующего тока.