4.3. Уравнения состояния цепей в комплексной форме

Пусть -я ветвь цепи содержит источники ЭДС и тока (рис .4.6).

Закон Ома такой ветви выглядит следующим образом

, .

Если число таких ветвей , то закон Ома пишут в матричной форме

, (4.1)

, (4.2)

здесь , , , – столбцовые матрицы напряжения, токов ветви, ЭДС и токов источников, например , , – матрицы комплексных сопротивлений и проводимостей ветвей,

. Для цепей, не содержащих взаимной индуктивности и электронных элементов, , – диагональные матрицы. Если ветвь содержит последовательно соединенные сопротивление, индуктивность и емкость, то

и .

Матрицы , , – диагональные, например

.

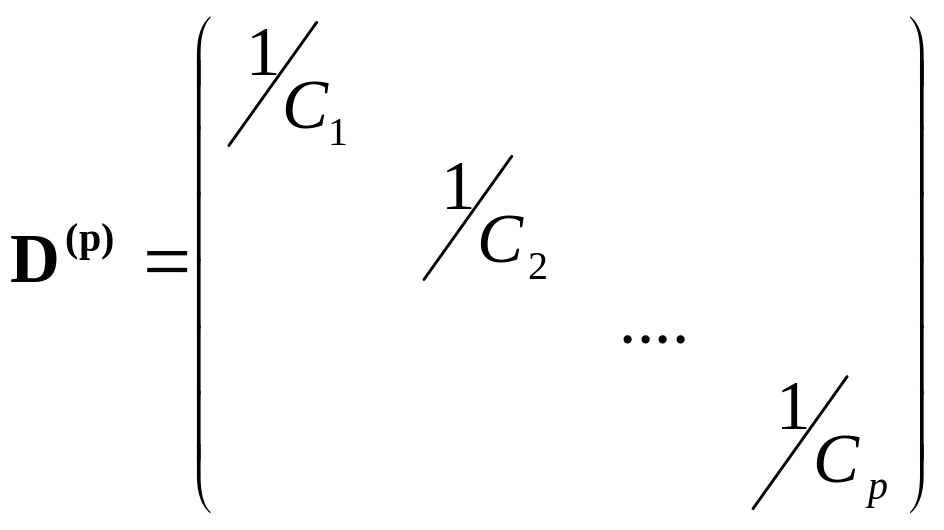Если ветвь содержит параллельно соединенные сопротивление, индуктивность и емкость, то

и .

Матрицы , , – диагональные, например

.

Уравнения Кирхгофа.

Уравнения по первому закону Кирхгофа для узлов

, (4.3)

где – матрица соединений порядка , .

Уравнения по первому закону Кирхгофа для сечений

, (4.4)

где – матрица сечений порядка , .

Матрицы и составляются для ориентированного графа схемы. Каждому из уравнений (4.3) и (4.4) соответствуют независимых алгебраических уравнений.

Уравнения по второму закону Кирхгофа

, (4.5)

где – матрица контуров порядка . Уравнению (4.5) соответствуют уравнений, которые являются независимыми.

Уравнения (4.3) и (4.5) или (4.4) и (4.5) вместе с (4.1) и (4.2) позволяют определять токи во всех ветвях цепи. Однако для расчета целесообразно видоизменить уравнения Кирхгофа следующим образом .

подставим в (4.31) и получим

. (4.6)

Произведение даст матрицу-столбец, элемент -ой строки этой матрицы равен сумме токов в сопротивлениях ветвей, присоединенных к “ ” узлу. При этом с положительным знаком записываем токи, направленные от узла. Произведение дает матрицу-столбец, элемент -ой строки этой матрицы равен сумме токов источников тока в ветвях, присоединенных к “ ” узлу. При этом с положительным знаком записывают токи, направленные к узлу.

Аналогично можем записать (4.4)

. (4.7)

Умножим обе части (4.1) на матрицу и учтем (4.5). Тогда

,

. (4.8)

Произведение дает матрицу-столбец, элемент -ой строки этой матрицы равен сумме напряжений на сопротивлениях ветвей, которые составляют -й контур.

Произведение дает матрицу-столбец, элемент -ой строки этой матрицы равен сумме ЭДС источников ЭДС в ветвях, подсоединенных к “ ” узлу.

Расчет цепей с помощью уравнений Кирхгофа сводится к совместному решению уравнений (4.6) и (4.8) или (4.7) и (4.8). Искомыми являются токи в сопротивлениях ветвей, то есть при известных , , .

, (4.9)

, (4.10)

где , столбцовые матрицы для комплексных потенциалов и токов в комплексной форме.

Узловые уравнения

, (4.11)

где матрица узловых проводимостей.

матрица узловых токов. Она определяется следующим образом

.

Контурные уравнения

, (4.12)

где – матрица контурных сопротивлений. .

матрица контурных ЭДС.

Аналогия между уравнениями цепей с источниками постоянных и синусоидальных ЭДС и токов позволяют сделать вывод, что все методы расчета, рассмотренные применительно к цепям постоянного тока, пригодны и для расчета цепей при синусоидальном токе.