
- •Часть 2 Учебное пособие
- •2. Свойства и методы расчета линейных цепей постоянного тока (продолжение)
- •2.10. Простейшие эквивалентные преобразования схем
- •2.11. Преобразование схем при исключении узлов.
- •2.12. Преобразование схем при исключении контуров
- •3. Свойства и методы расчета цепей синусоидального тока.
- •3.1. Синусоидальный ток.
- •3.2. Установившийся режим в цепи с последовательным соединением , и (рис. 3.3)
- •3.3. Установившийся режим в цепи с параллельным соединением , и (рис. 3.7).
- •3.4. Активная, реактивная и полная мощность цепи синусоидального тока
- •3.5. Мгновенная мощность.
- •Эквивалентные параметры сложной цепи.
- •3.7. Связь между сопротивлением и проводимостью
- •4. Основы комплексного метода расчета цепей синусоидального тока
- •4.1. Расчет простых цепей синусоидального тока.
- •4.2. Топографическая диаграмма
- •4.3. Уравнения состояния цепей в комплексной форме
- •4.4. Основные свойства и преобразование цепей синусоидального тока.
- •5. Индуктивно-связанные цепи
- •5 .1. Эдс самоиндукции и взаимоиндукции
- •5.2. Взаимная индуктивность при последовательном соединении
- •5.3. Взаимная индуктивность при параллельном включении
- •5.4. Расчет сложных индуктивно-связанных цепей.
- •5.5. Трансформаторы с линейными характеристиками.
- •6. Трехфазные цепи
- •4.1. Многофазные цепи и системы
- •6.2. Соединение звездой
- •6.3. Соединение треугольником
- •6.4. Разложение несимметричных трехфазных систем на симметричные составляющие.
4. Основы комплексного метода расчета цепей синусоидального тока
Расчет цепей синусоидального тока связан с операциями сложения (вычитания) синусоидальных величин с различными амплитудами и различными начальными фазами. Хотя эти операции просты, они приводят к громоздким вычислениям, степень сложности которых нарастает с усложнением структуры электрических цепей. Поэтому в расчетах цепей синусоидального тока пользуются комплексным методом. Суть метода состоит в том, что синусоидальная величина заменяется комплексной и все действия над синусоидальными величинами заменяются действиями над комплексными величинами. При этом расчет электрических цепей существенно упрощается.
Допустим, что
имеются синусоидальный ток
![]() и комплексное число
и комплексное число
![]() .
Видно, что синусоидальный
ток
совпадает с коэффициентом мнимой части
комплексного числа
.
Видно, что синусоидальный
ток
совпадает с коэффициентом мнимой части
комплексного числа
![]() .
Это дает нам основание рассмотреть
указанное комплексное число как
изображение синусоидального
тока.
.
Это дает нам основание рассмотреть
указанное комплексное число как
изображение синусоидального
тока.
![]() .
.
Так
как
![]() ,
где
,
где
![]() - комплексная амплитуда.
- комплексная амплитуда.
Рассмотрим операцию дифферинцирования
![]() ,
,
![]() .
.
Таким
образом, операция дифференцирования
синусоидальной величины состоит в
умножении ее комплексного изображения
на
![]() .
.
Рассмотрим операцию интегрирования
![]() ,
,
![]() .
.
Операция интегрирования синусоидальной величины состоит в делении ее комплексного изображения на .
![]() ,
,
![]() ,
,
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() –
комплексные действующие значения тока,
ЭДС, напряжения или просто комплексный
ток, комплексная ЭДС, комплексное
напряжение.
–
комплексные действующие значения тока,
ЭДС, напряжения или просто комплексный
ток, комплексная ЭДС, комплексное
напряжение.
Комплексное сопротивление равно
![]() ,
,
![]() .
.
Комплексная мощность определяется следующим образом
![]() .
.
4.1. Расчет простых цепей синусоидального тока.
а) последовательное соединение участков.
Рассчитаем цепь, схема которой показана на рис. 4.1.
К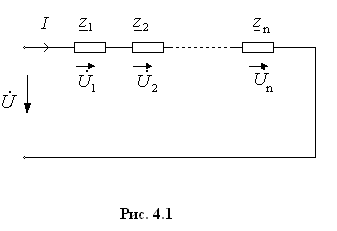 аждое
сопротивление состоит из активной и
реактивной части
аждое
сопротивление состоит из активной и
реактивной части
![]() ,
,
![]() .
.
Учтем последовательное соединение и запишем
![]() .
Отсюда
.
Отсюда
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() .
.
Можно заключить, что при последовательном соединении участков комплексное сопротивление всей цепи равно сумме комплексных сопротивлений отдельных участков.
б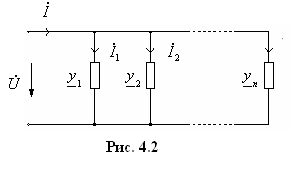 )
параллельное соединение участков (рис.
4.2).
)
параллельное соединение участков (рис.
4.2).
По аналогии с предыдущим случаем получаем
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
При параллельном соединении участков комплексная проводимость всей цепи равна сумма комплексных проводимостей отдельных участков.
в) смешанное соединение участков (сочетание последовательного и параллельного соединений участков).
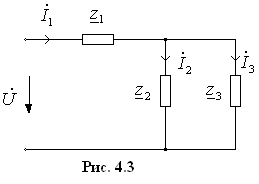 Рассчитаем
цепь, схема которой показана на рис.
4.3.
Рассчитаем
цепь, схема которой показана на рис.
4.3.
![]() ;
;
![]() ;
;
![]() ,
,
![]() ;
;
![]() .
.
4.2. Топографическая диаграмма
 Каждой
точке цепи соответствует определенный
потенциал. В цепи синусоидального тока
потенциал также как и ток, напряжение
можно представить в виде комплексного
числа и соответственно изобразить его
вектором на комплексной плоскости.
Векторную диаграмму комплексных
потенциалов схемы называют топографической
диаграммой. Каждой точке схемы
соответствует определенная точка
топографической диаграммы. Базовому
узлу схемы, потенциал которого принят
равным нулю, на топографической диаграмме
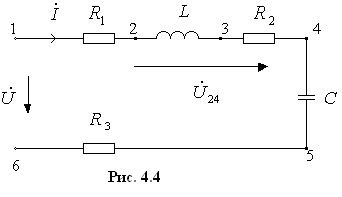
соответствует началу координат. Имеем
схему на рис. 4.4. За базовый узел принимаем
точку 6 (
Каждой
точке цепи соответствует определенный
потенциал. В цепи синусоидального тока
потенциал также как и ток, напряжение
можно представить в виде комплексного
числа и соответственно изобразить его
вектором на комплексной плоскости.
Векторную диаграмму комплексных
потенциалов схемы называют топографической
диаграммой. Каждой точке схемы
соответствует определенная точка
топографической диаграммы. Базовому
узлу схемы, потенциал которого принят
равным нулю, на топографической диаграмме
соответствует началу координат. Имеем
схему на рис. 4.4. За базовый узел принимаем
точку 6 (![]() ).
Обход контура производим в направлении,
противоположном направлению тока.
).
Обход контура производим в направлении,
противоположном направлению тока.
![]()
 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
На топографической
диаграмме (рис. 4.5) векторы напряжений
между любыми двумя точками имеют
направления, противоположные направлениям
напряжений относительно соответствующих
точек на схеме. Например, на схеме
![]() (направление от 2 к 4), на топографической
диаграмме вектор направлен от 4 к 2, что
объясняется правилом вычитания векторов:
разность векторов всегда направлена в
сторону уменьшаемого вектора.
(направление от 2 к 4), на топографической
диаграмме вектор направлен от 4 к 2, что
объясняется правилом вычитания векторов:
разность векторов всегда направлена в
сторону уменьшаемого вектора.
