3.3. Установившийся режим в цепи с параллельным соединением , и (рис. 3.7).

П усть , .

,

П о первому закону Кирхгофа

,

или

. (3.2)

Это выражение справедливо при любом .

Рассмотрим следующие случаи:

,

.

Отсюда , .

Здесь – активная проводимость, – индуктивная проводимость, – емкостная проводимость, – реактивная проводимость,

– полная проводимость.

Таким образом , .

Построим векторную диаграмму (рис. 3.8). Для этого перепишем (3.2)

.

Получили треугольник токов. Поделив стороны этого треугольника на , получим треугольник проводимостей (рис. 3.9).

3.4. Активная, реактивная и полная мощность цепи синусоидального тока

Мгновенная мощность – это произведение мгновенного значения напряжения и тока:

.

А ктивная мощность – это среднее значение мгновенной мощности за период:

.

Пусть , . Тогда

,

, здесь – коэффициент мощности

Р еактивная мощность определяется по формуле .

Полная мощность равна .

Построим треугольник мощности (рис. 3.10).

Найдем другие формулы для , и . Используем треугольники напряжений и токов (рис. 3.11, 3.12).

, , .

3.5. Мгновенная мощность.

Предположим, что цепь, схема которой показана на рис. 3.13, подключена к синусоидальному напряжению . В цепи начинает протекать ток . В соответствии с II законом Кирхгофа можно записать . Умножим на ток и получим или

,

где

,

,

,

,

.

Мгновенная мощность цепи равна

.

Отсюда видно:

1) мгновенная мощность индуктивного элемента изменяется по синусоидальному закону с двойной частотой,

2) также изменяется мгновенная мощность емкостного элемента. Однако указанные мощности находятся в противофазе,

3) мгновенная мощность активного элемента имеет постоянную составляющую и переменную составляющую, изменяющуюся с частотой ,

4) мгновенная мощность всей цепи имеет постоянную составляющую и переменную составляющую, изменяющуюся с частотой .

Временные зависимости рассмотренных мощностей приведены на рис. 3.14.

Рассмотренная цепь называется неуравновешенной, т.к. ее мгновенная мощность зависит от времени.

6. Эквивалентные параметры сложной цепи.

П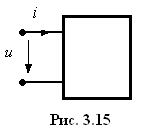 усть сложная цепь представлена пассивным двухполюсником (рис. 3.15). Нас интересует ток на входе в двухполюсника. Как в этом случае можно представить эквивалентную схему двухполюсника?

Пусть известны величины на входе двухполюсника: , и .

Р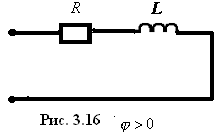 ассчитаем сопротивления , Зная и можно вычислить реактивное сопротивление , при этом:

, if , , (Fig. 3.16),

, if , , (Fig. 3.17).

Тогда двухполюсник можно представить одной из цепей (рис. 3.16, рис. 3.17):

М ожно записать , .

Зная и можно вычислить реактивную проводимость: , при этом

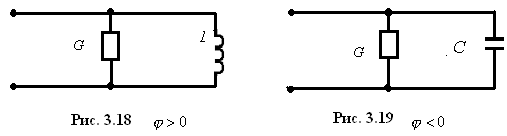
, если то или , если то . Эквивалентные схемы для этих случаев показаны на рис. 3.18 и рис. 3.19.

3.7. Связь между сопротивлением и проводимостью

Согласно закону Ома , отсюда , .

И з треугольника сопротивлений (рис. 3.20) получаем

, .

Из треугольника проводимостей (рис. 3.21) получаем

, .

Таким образом, имеем

, , and , , .