3. Свойства и методы расчета цепей синусоидального тока.

3.1. Синусоидальный ток.

Переменным током называется ток, величина которого изменяется во времени. Среди возможных законов изменения тока наибольший интерес представляет синусоидальный закон. При синусоидальном токе потери электрической энергии в генераторах и передающих устройствах, а также в приемниках электрической энергии оказываются меньше, чем при токах, изменяющихся по любому другому периодическому закону.

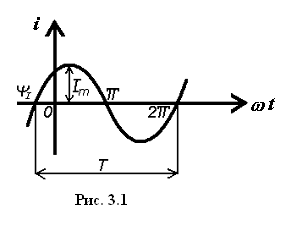
Синусоидальный ток (рис. 3.1) определяется формулой

,

где – мгновенное значение тока, – его амплитуда, – круговая частота, , – частота ( ), – период, – начальная фаза.

Аналогично определяются синусоидальные ЭДС и напряжение.

, ,

где , – мгновенные значения ЭДС, напряжения, , – их амплитуды, , – начальные фазы.

Кроме мгновенных и амплитудных значений, синусоидальные величины характеризуются еще средне-квадратичным значением их за период, то есть

, , .

, и называются действующими значениями тока, ЭДС и напряжения. Пусть , тогда

.

Таким образом , , .

Среднее значение за полупериод определяется формулой .

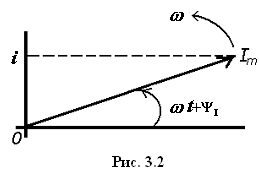
Синусоидальные величины, имеющие угловую частоту , можно изобразить векторами, вращающимися против часовой стрелки со скоростью (рис. 3.2). Длина вектора в определенном масштабе равна амплитуде синусоидальной величины. Пусть имеем . Видно, что мгновенный ток равен проекции вектора на ось ординат.

Совокупность векторов, построенных с учетом их взаимной ориентации, характеризует процессы в цепи, и называется векторной диаграммой. Векторная диаграмма строится либо для амплитудных, либо для действующих значений токов, ЭДС, напряжений.

3.2. Установившийся режим в цепи с последовательным соединением , и (рис. 3.3)

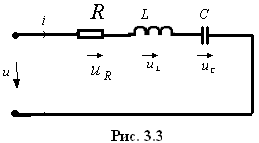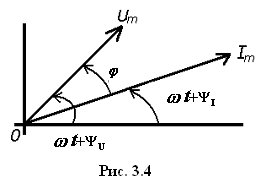
П усть , искомый ток можно представить в виде . Значение имеет фазовой угол между током и напряжением, то есть . Можно положить . Тогда и задача ставится так: действует напряжение , необходимо найти ток , то есть , (рис. 3.4).

Запишем уравнение по второму закону Кирхгофа:

, или

, или

. Это уравнение справедливо при любом .

,

.

Отсюда

; .

Здесь – активное сопротивление ( этот параметр характеризует необратимые процессы преобразования электрической энергии в тепло). – индуктивное сопротивление (этот параметр характеризует синусоидальное изменение магнитного поля, сцепленного с цепью). – емкостное сопротивление (этот параметр характеризует синусоидальное изменение электрического поля в цепи). – реактивное сопротивление. – полное сопротивление. Таким образом, имеем

, .

Построим векторную диаграмму. Для этого перепишем

.

Начертим треугольник напряжений (рис. 3.5). Из него видно:

1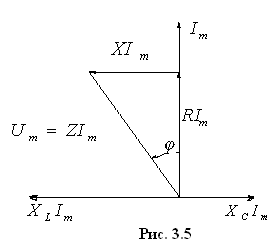 ) в активном сопротивлении ток и напряжение совпадают по фазе;

2) в индуктивности ток отстает от напряжения на угол ;

3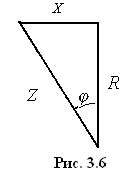 ) в емкости ток опережает напряжение на угол .

Разделив все стороны треугольника напряжений на , получим треугольник сопротивлений (рис 3.6).