2.12. Преобразование схем при исключении контуров
Матричное контурное уравнение (2.21) запишем в виде
.
(2.63)
Отсюда получаем
Пусть
- неособенная квадратная матрица. Тогда
.
Данное выражение вносим во второе уравнение
.
Обозначим
следующим образом
,
(2.64)
.
(2.65)
Тогда получим
.
(2.66)
Пусть
- неособенная квадратная матрица. Тогда
,
(2.67)
где
,
(2.68)
.
(2.69)
Уравнения
(2.66) и (2.67) – контурные уравнения
эквивалентных схем, полученных исключением
контуров. Токи в этих контурах образуют
матрицу
или матрицу
.
Эквивалентные схемы имеют контурные
токи, совпадающие с токами матриц
или
.
Пусть
схема имеет k
независимых контуров и k-й
контур исключается. Тогда матрицу
контурных сопротивлений
исходной схемы делят на блоки следующим
образом:
,
где
Матрицу
контурных сопротивлений схемы с
исключенным контуром вычислим по (2.68)
при
(2.70)
Отсюда получаем собственные сопротивления j-го контура (j=1, 2,..,k-1)
.
Общее сопротивление i-го и j-го контуров (j=1, 2,…,k-1) равно
.
Если
i-й
и j-й
контуры не имеют общих сопротивлений
с исключенным контуром
,
то собственные сопротивления
и общее сопротивления
при исключении k-ого
контура не изменяются.
Матрицу
контурных ЭДС исходной схемы представим
в виде
,
где
,
.
Согласно (2.69) матрица контурных ЭДС схемы с исключенным контуром равна
.
(2.71)
Отсюда видно, что при исключении k-ого контура ЭДС j-ого контура равна
.
В общем случае по матрице контурных сопротивлений (2.70) не удается составить эквивалентную схему обычного вида, т.к. при числе контуров больше трех, такая схема не имеет общих сопротивлений для каждой пары контуров.
Для иллюстрации преобразования схемы путем исключения контуров можно ввести условную эквивалентную схему, в которой каждый контур исходной схемы изображается отдельно.
Пример.
Необходимо
исключить контур с током
в схеме на рис. 2.46.
Для исходной семы составляем условную эквивалентную схему (рис. 2.47).
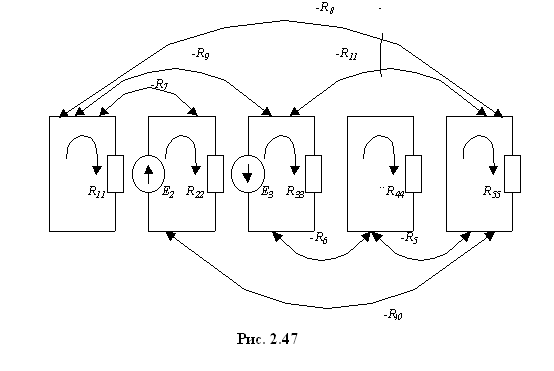
Матрица контурных сопротивлений исходной схемы выглядит следующим образом
,
где
Если исключаем контур, получим согласно (2.70) матрицу контурных сопротивлений новой схемы
=
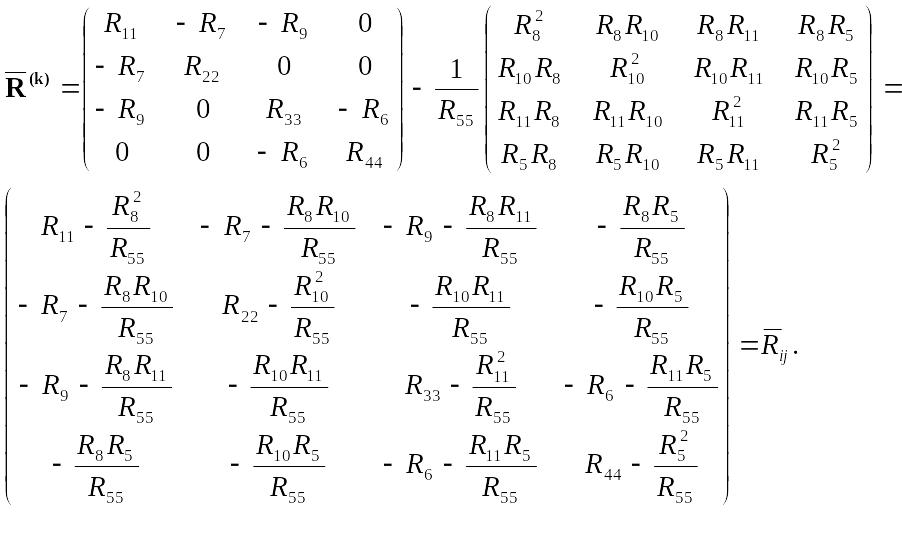
Согласно
(2.71) имеем
М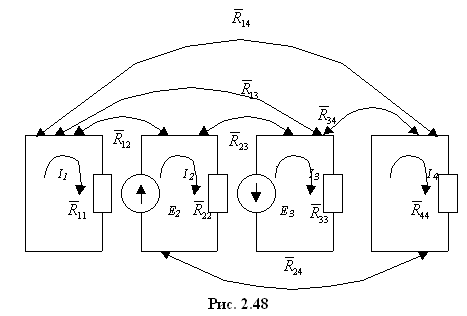
атрицам
и
соответствует условная эквивалентная
схема (рис. 2.48).
Здесь
и
т.д.
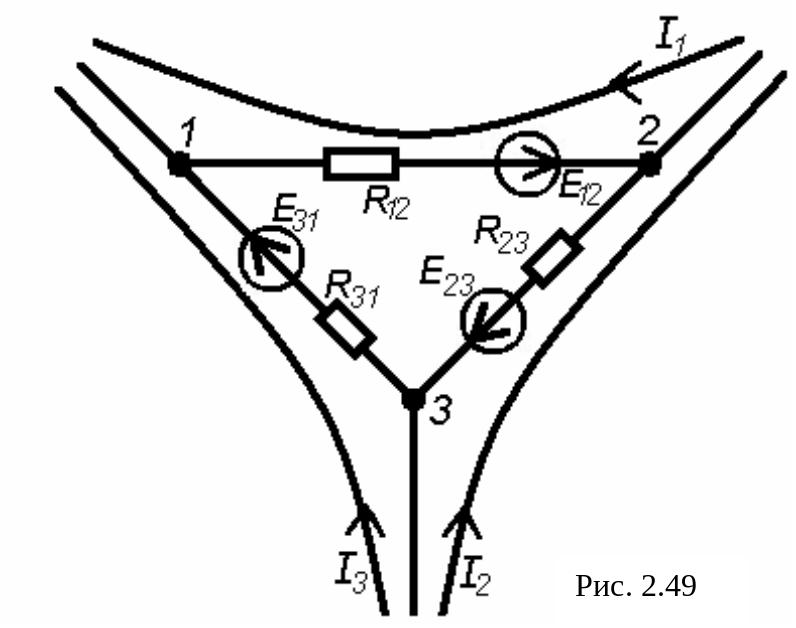
Частным случаем преобразования схемы при уменьшении числа контуров является преобразование треугольника (рис. 2.49) сопротивлений в эквивалентную звезду (рис. 2.50).
Д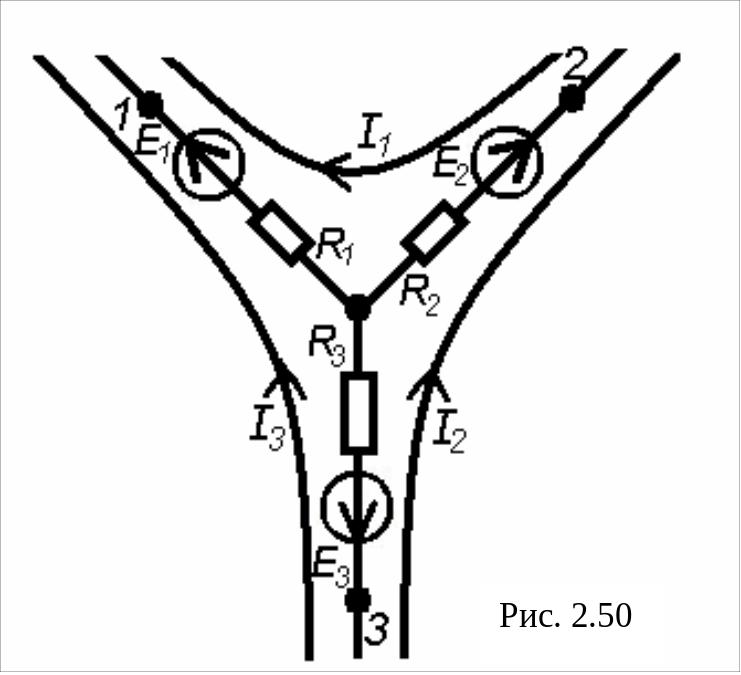
ля
треугольника справедливо уравнение
где
-
неопределенная матрица контурных
сопротивлений
,
- матрица
контурных токов,
- матрица контурных ЭДС, где число
равно
.
Для пассивных параметров звезды, эквивалентной треугольнику из (2.61) и (2.62) находим
,
,
, (2.72)
(2.73)
При
исключении контура с током
в схеме треугольника матрица
преобразуется к виду, получаемому из
(2.48) при m=3
.
Для определения активных параметров звезды следует приравнять
Из
этих уравнений только два независимых,
поэтому задача определения ЭДС звезды
решается неоднозначно. Можно задать
значение одной из ЭДС. Если
,
то
;
.
Преобразование
полного многоугольника с числом узлов
в q-лучевую
звезду в общем случае невозможно, т.к.
число искомых проводимостей ветвей
звезды меньше числа условий, которым
они должны удовлетворять.