6.2. Соединение звездой

Соединим в общую точку концы фазных обмоток генератора. Эта точка (0) называется нейтральной точкой генератора (рис. 6.6). В общую точку объединим и концы приемников. Эта точка (0^/) называется нейтральной точкой приемника. Для передачи энергии от генератора приемнику нужно соединить соответственно фазы генератора и приемника. Провода, соединяющие начала фаз генератора с приемником, называются линейными проводами. Провод, соединяющий нейтральные точки генератора и приемника, называется нейтральным. Токи в фазах генератора и приемника называются фазными, а токи в линейных проводах – линейными токами. Напряжения между нейтральной точкой и началами фаз называют фазными напряжениями генератора. Аналогично определяются и фазные напряжения приемника. Напряжения между линейными проводами называются линейными напряжениями.

Е сли фазные токи образуют симметричную систему (прямой последовательности), то Поэтому нейтральный провод можно удалить. При не симметрии токов в фазах , но он меньше фазных токов, поэтому нейтральный провод можно сделать меньшего сечения, чем линейные провода.

Найдем связь между фазными и линейными величинами.

а) фазные токи равны линейным,

б)

При синусоидальных напряжениях и токах для комплексных действующих значений получим

.

Отсюда следует, что сумма линейных напряжений равна нулю.

Векторная диаграмма приведена на рис. 6.7.

Если системы напряжений и токов симметричны, то

.

Активная и реактивная мощности определяются следующим образом

6.3. Соединение треугольником

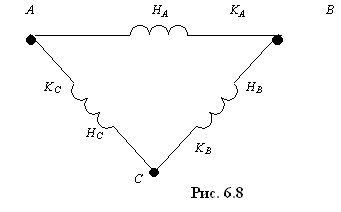
Соединим в генераторе конец каждой фазы с началом следующей фазы (рис. 6.8). Такое же соединение выполним и в приемнике. Передача энергии производиться с помощью трех линейных проводов (рис. 6.9). В этом случае справедливы следующие соотношения:

а) фазные напряжения равны линейным.

б)

или

Отсюда следует, что сумма линейных токов равна нулю

.

Векторная диаграмма показана на рис. 6.10.

Если системы напряжений и токов симметричны, то

.

Мощности определяются по формулам:

6.4. Разложение несимметричных трехфазных систем на симметричные составляющие.

Несимметричные трехфазные системы ЭДС, напряжений, токов можно представить в виде суммы симметричных систем нулевой, прямой и обратной последовательности. Эти системы обычно называются симметричными составляющими. Рассмотрим несимметричную трехфазную систему ЭДС , , (рис. 6.11). Представим ЭДС каждой фазы в виде суммы слагаемых в виде

(6.1)

В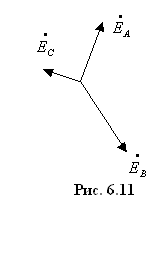 ектора , , равны по величине и совпадают по фазе, следовательно, они образуют систему нулевой последовательности.

Вектора , , можно представить следующим образом (рис. 6.12)

В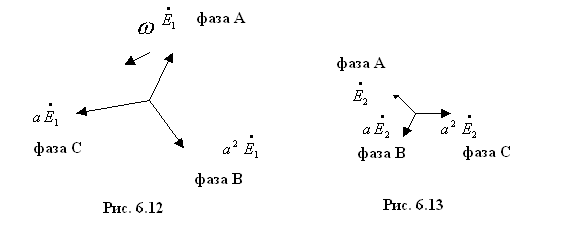 ектора , , изображаются следующим образом. Т.е. они образуют систему обратной последовательности (рис. 6.13).

Термин “симметричные составляющие” относят не только к симметричным системам нулевой ( , , ), прямой ( , , ) и обратной последовательности ( , , ), но и к основным комплексам , , , на которые распадаются ЭДС в фазе А.

Найдем симметричные составляющие , , . Используем систему (6.1). Т.к. главный определитель этой системы уравнений

,

то , , определяются однозначно.

Имеем, т.к. и , систему (6.2)

(6.2)

Симметричные составляющие , , можно определить графически.

Согласно (6.2) для определения нужно сложить все три вектора и результат разделить на 3 (рис. 6.15).

Несимметричные системы напряжений и токов также разлагаются на симметричные составляющие. При этом эти составляющие определяются по формулам (6.2), в которых ЭДС заменяются на напряжения или токи.

Из (6.2) следует, что составляющая нулевой последовательности в системе линейных напряжений будет отсутствовать (рис. 6.16).

.

Составляющей нулевой последовательности не будет и система токов в трехфазных цепях без нейтрального провода.

.

ЛИТЕРАТУРА

Основная

1. Нейман Л.Р., Демирчян К.С. ТОЭ. - Л.: Энергоиздат, 1981. - Т. 1,2.

2. Теоретические основы электротехники. Под ред. П.А. Ионкина. Т. 1,2. - М.: ВШ., 1976.

3. Теоретические основы электротехники. Под ред. Г.И. Атабекова. Т. 1,2 - М.: Энергия, 1979.

4. Сборник задач и упражнений по ТОЭ. Под ред. П.А. Ионкина. - М.: Энергоиздат, 1982. - 766с.

5. Пашенцев И.Д. Методические пособия по решению задач курса ТОЭ. - Л.: ЛИИЖТ, 1981. - Ч. I-VI.

6. Бессонов Л.А. Сборник задач по ТОЭ. - М.: ВШ, 1988.

7. Бессонов Л.А. Теоретические основы электротехники. - М.: ВШ, 1978. - Т.1,2.

8. Новгородцев А.Б. 30 лекций по теории электрических цепей. - СПб.: Политехника, 1995. - 519с.

9. Шимони К. Теоретическая электротехника. - М.: МИР, 1964. - .773с.

10. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. - М.: Энергоиздат, 1989. - 333с.

11. Белецкий А.Ф. Теория линейных электрических цепей. - М.: Радио и связь, 1986. - 554с.

12. Поливанов К.М. Теоретические основы электротехники. - М.: Энергия, 1975. - Т.3. - 352с.

13. Литература информационно-методического обеспечения учебного процесса, разработанная кафедрой ТОЭ.

Дополнительная

1. Матханов П.Н. Основы анализа электрических цепей. - М.: ВШ, 1990

2. Практикум по ТОЭ. Под ред. Шакирова М.А. - СПб.: СПбГТУ, 1995. - Ч. 1,2,3

3. Шебес М.Р. Задачник про теории линейных электрических цепей. - М.:ВШ, 1973. - 655с.

4. Демирчян К.С., Бутырин П.Л. Моделирование и машинный расчет электрических цепей. - М.: ВШ, 1988.

5. Кухаркин Е.С. Основы технической электродинамики. - М.: ВШ, 1969 - Ч. 1,2.

Рекомендуется использование программ, сочетающих в себе необходимость понимания физических явлений при постановке задачи исследования электромагнитных процессов и минимальности затрат времени на реализацию ее решения на компьютере, включая использования пакетов программ Pspice, Workbench, Matlab, Mathcad.

59