ПЕТЕРБУРГСКИЙ

Г ОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

K.K. Kим

САМОУЧИТЕЛЬ ПО ТЕОРИИ ЛИНЕЙНЫХ

ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Часть 2 Учебное пособие

Санкт-Петербург

2005

УДК 621.3.01

ББК 31.211

Kим K.K.

Самоучитель по теории линейных электрических цепей. Ч.2: Учебное пособие . – СПб.: Петербургский государственный университет путей сообщения, 2005. – 60 с.

Библ.: 18. Fig. 70.

Основные проблемы теории и расчета линейных электрических цепей рассмотрены в данном пособии.

Учебное пособие написано в соответствии с дисциплиной «Теоретические основы электротехники» и является продолжением учебного пособия К.К. Кима «Самоучитель по теории линейных электрических цепей», ч.1. Поэтому нумерация рисунков и формул выполнена в соответствии с нумерацией предыдущего пособия. Пособие предназначено для студентов-заочников электромеханических и электротехнических специальностей.

Пособие может быть полезно инженерам и аспирантам.

 K.K. Kим, 2005

Если хочешь быть красивым, поступи в гусары.

Если хочешь быть умным, поступи на Заочный факультет!

Козьма Прутков (из неизданного)

2. Свойства и методы расчета линейных цепей постоянного тока (продолжение)

2.10. Простейшие эквивалентные преобразования схем

Анализ сложных электрических цепей можно упростить путем различных преобразований схем. Целесообразное преобразование схемы приводит к уменьшению числа узлов, контуров и ветвей, а, следовательно, к уменьшению числа уравнений, характеризующих сложные электрические схемы.

П реобразования называются эквивалентными, если выполнено условие неизменности токов и напряжений ветви в тех частях схемы, которые не затронуты преобразованиями.

Предположим, что в схеме (рис. 2.36) имеется параллельно соединенных ветвей с источниками ЭДС, источниками токов и сопротивлениями. Заменим их одной ветвью. Для данной схемы справедливо узловое уравнение

, ,

, так как узел 2 – опорный узел ( ).

Отсюда , где , .

П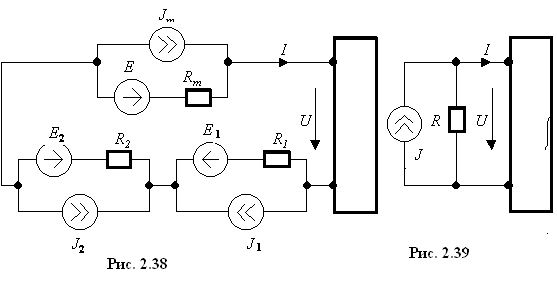 оследним соотношениям соответствует схема на рис. 2.37. Таким образом, схему на рис. 2.36 можно заменить схемой на рис. 2.37; при этом ток и напряжение в этих схемах соответственно одинаковы. При определении эквивалентного источника ЭДС слагаемые и алгебраически суммируются: с положительным знаком записывают ЭДС и токи источников, направленные к узлу 1, в противном случае – со знаком минус. В числителе (формула для ) слагаемые, соответствующие ветвям, не содержащим эквивалентных источников ЭДС и тока, отсутствуют; в знаменателе (формула для и ) записывают сумму проводимостей всех ветвей.

По аналогии последовательное соединение ветвей, содержащих источники тока, ЭДС и сопротивления (рис. 2.38) заменяют одной ветвью с источником тока и сопротивлением (рис. 2.39).

.

Отсюда , где , .

Если схема содержит смешанные соединения ветвей, содержащие источники, для расчета можно использовать вышеприведенные преобразования.

Любую схему, содержащую источники ЭДС и тока, можно преобразовать в схему, имеющую только источники тока или только источники ЭДС. Если схема содержит ветви идеальные источники ЭДС или идеальные источники тока, то применяют преобразование источников.

При преобразовании схем с источниками энергии суммарные мощности источников и приемников в исходных схемах не равны в общем случае соответствующим мощностям в эквивалентных схемах.

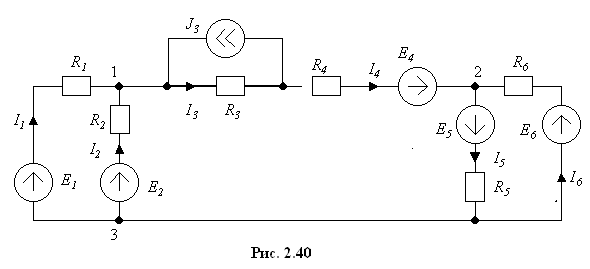
Пример.

Рассчитать токи в ветвях схемы, показанной на рис. 2.40. Дано: , , , , , , , , .

Заменим две ветви с источниками ЭДС и одной ветвью с эквивалентным источником с ЭДС

и эквивалентным сопротивлением

.

Д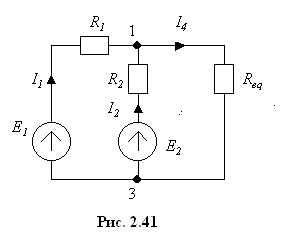 алее три последовательные ветви (с источниками , и ) заменим одной ветвью с источником ЭДС

и сопротивлением

.

в результате получим схему, приведенную на рис. 2.41.

Если допустить, что , то .

Токи в ветвях равны: , , ,

.

Найдем потенциал узла 2 . Далее находим токи ; .