ПЕТЕРБУРГСКИЙ

Г ОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ

СООБЩЕНИЯ

K.K. Kим, г.Н. Анисимов

ЭЛЕКТРОТЕХНИЧЕСКИЕ СРЕДСТВА ИЗМЕРЕНИЙ

Часть 2 Учебное пособие

Санкт-Петербург

2006

УДК 621.317.39

ББК 31.221

Kим k.K., Анисимов г.Н.

Электротехнические средства измерений. Ч.2: Учебное пособие . – СПб.: Петербургский государственный университет путей сообщения, 2006. – 60 с.

Библ.: 6. Рис. 34. Табл. 1

Приведены сведения по классификации электротехнических средств измерений. Рассмотрены принципы действия, устройство, назначение и эк4сплуатационные свойства электротехнических средств измерения.

Настоящее издание предназначено для студентов технических специальностей заочной формы обучения, самостоятельно изучающих дисциплину «Метрология, стандартизация и сертификация», а также работников метрологических служб предприятий Министерства транспорта.

 K.K. Kим, Г.Н. Анисимов, 2006

ОГЛАВЛЕНИЕ

С. 5. Магнитоэлектрические измерительные механизмы и приборы…… 5.1. Применение магнитоэлектрических измерительных механизмов для измерений в цепях переменного тока……………………………… 6. Индукционные приборы……………………………………………… 7. Приборы сравнения…………………………………………………… 7.1. Общие сведения…………………………………………………… 7.2. Общая теория мостовых схем………………………………………. 7.3. Мосты постоянного тока……………………………………………. 7.4. Мосты переменного тока…………………………………………… 7.5. Компенсаторы………………………………………………………... 8. Приборы для измерения и регистрации изменяющихся во времени величин……………………………………………………… 8.1. Назначение и классификация средств регистрирующей техники……………………………………………………………………. 8.2. Виды регистрации измерительной информации………………….. 8.3. Самопишущие приборы…………………………………………….. 8.4. Светолучевые осциллографы………………………………………. Литература……………………………………………………………….. 4 16 32 36 36 38 41 44 50 54 54 55 56 58 60

5. Магнитоэлектрические измерительные механизмы и приборы.

О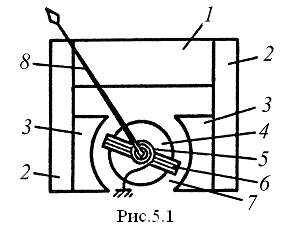 бщие сведения. В магнитоэлектрических измерительных механизмах вращающий момент создается в результате взаимодействия магнитного поля постоянного магнита и проводника с током, выполняемого обычно в виде катушки-рамки, по которой протекает измеряемый ток.

Основными узлами магнитоэлектрического измерительного механизма являются магнитная система и подвижная часть. Конструктивно различают магнитоэлектрические механизмы с подвижной катушкой и с подвижным магнитом. Наиболее распространен механизм с подвижной катушкой. В свою очередь измерительные механизмы с подвижной катушкой делятся на механизмы с внешним магнитом и с внутренним магнитом.

По способу создания противодействующего момента магнитоэлектрические измерительные механизмы подразделяются на измерительные механизмы с механическим противодействующим моментом и с электрическим противодействующим моментом (логометры).

Момент успокоения создается магнитоиндукционным путем (без применения специальных успокоителей) за счет взаимодействия токов, наводимых в дюралюминиевом каркасе подвижной катушки и в цепи самой катушки, с полем постоянного магнита.

Условные обозначения магнитоэлектрических приборов представлены в табл. 4.1. По существующей классификации в названии типа прибора им присвоена буква М (например, М197).

Магнитоэлектрические измерительные механизмы с механическим противодействующим моментом. На рис. 5.1 показано устройство магнитоэлектрического измерительного механизма с подвижной катушкой и внешним магнитом, где 1 – постоянный магнит, 2 – магнитопровод, 3 – полюсные наконечники, 4 – неподвижный сердечник, 5 – спиральная пружина, 6 – подвижная катушка, 7 – рабочий воздушный зазор, 8 – указатель. Ток к подвижной катушке подводится через две спиральные пружины. При протекании через подвижную катушку тока i возникает вращающий момент, мгновенное значение которого M_{вр t} определяется выражением (4.2). Катушка перемещается в узком воздушном зазоре толщиной порядка 1 ÷ 2 мм, в котором создается радиальное магнитное поле с постоянной величиной магнитной индукции B. В этом случае магнитный поток, сцепляющийся с обмоткой, будет определяться выражением

Φ = BSα ,

где S – площадь катушки-рамки, α – угол поворота катушки (подвижной части).

Энергия электромагнитного поля, сцепляющегося с подвижной катушкой, с учетом энергии, запасаемой в самой катушке, определится выражением

W_эм = Ψi + ,

где Ψ = Φw = BSwα – потокосцепление подвижной катушки, w – число витков обмотки катушки, L – собственная индуктивность катушки. Поскольку от угла поворота катушки α зависит только потокосцепление Ψ, то для вращающего момента после дифференцирования согласно (8.2) получим

M_{вр t} = BSwi . (5.1)

Противодействующий момент M_пр создается пружиной и определяется выражением (4.3). Из условия уравновешивания вращающего и противодействующего моментов при установившимся отклонении подвижной части

M_{вр t} + M_пр = 0 (5.2)

с учетом (5.1) получим для угла поворота подвижной части

α = = S_I i , (5.3)

где S_I = BSw/W – чувствительность измерительного механизма к току.

Из выражения (5.3) следует, что магнитоэлектрический измерительный механизм с механическим противодействующим моментом непосредственно является измерителем тока. Кроме того, поскольку S_I есть величина постоянная, независящая от измеряемой величины и угла поворота подвижной части, прибор будет иметь равномерную шкалу.

При протекании через катушку постоянного тока I вращающий момент и угол поворота подвижной части соответственно будут равны

M_вр = BSwI , α = = S_I I . (5.4)

Если ток синусоидальный (i = I_m sin ωt), то мгновенное значение вращающего момента M_{вр t} = BSwI_m sin ωt. Учитывая, что у магнитоэлектрических измерительных механизмов период собственных (свободных) колебаний подвижной части приблизительно одна секунда (частота собственных колебаний ω₀ = 6,28 с^-1), на частотах свыше 10 Гц она в силу своей инерционности не будет успевать реагировать на изменения тока. Вследствие этого, угол поворота подвижной части будет определяться средним за период T значением вращающего момента

M_вр = dt . (5.5)

Таким образом, при синусоидальном токе M_вр и, соответственно, угол поворота подвижной части α равны нулю. Поэтому для измерений на синусоидальном токе магнитоэлектрические измерительные механизмы не применяют.

Если по катушке протекает периодический ток с периодом T несинусоидальной формы, который аналитически может быть представлен в виде разложения в ряд Фурье по гармоническим составляющим

i = I₀ + sin (kωt + ψ_k) , (5.6)

где I₀ – постоянная составляющая, k – номер гармоники, I_mk – амплитуда k-ой гармоники, ω = , ψ_k – начальная фаза k-ой гармоники, то согласно (5.5) и учитывая анализ, проведенный для постоянного и синусоидального токов, получим для среднего значения вращающего момента и угла поворота подвижной части соответственно следующие выражения:

M_вр = BSwI₀ , α = I₀ , (5.7)

т. е. при протекании по катушке переменного несинусоидального тока магнитоэлектрический прибор будет измерять постоянную составляющую.

Область применения. Магнитоэлектрические измерительные механизмы с механическим противодействующим моментом применяются главным образом в амперметрах и вольтметрах постоянного тока, гальванометрах, а также в некоторых типах омметров.

В амперметрах измерительный механизм включается в цепь непосредственно или с помощью шунта. Непосредственное включение (без шунта) применяется при измерении токов, допустимых для токоподводящих пружинок (или растяжек) и обмотки катушки-рамки подвижной части измерительного механизма. Значение таких токов не превышает 30 мА, т. е. непосредственное включение характерно только для микро- и миллиамперметров. В остальных случаях в амперметрах используют шунты. В многопредельных амперметрах используют многопредельные шунты. Амперметры выпускают с верхним пределом измерений от 10^-7 до 7500 А.

В вольтметрах последовательно с измерительным механизмом включается добавочный резистор, и это соединение подключается к тем точкам схемы, между которыми необходимо измерить напряжение. В многопредельных вольтметрах используют несколько добавочных резисторов. Вольтметры выпускают с верхним пределом измерений от 0,5 мВ до 3000 В.

С точки зрения применения амперметры и вольтметры выпускают переносными и щитовыми. Переносные приборы в большинстве случаев делают высокоточными (классов 0,1 – 0,5), многопредельными и часто комбинированными. Щитовые приборы, как правило, выпускают однопредельными, чаще всего классов точности 1,0 и 1,5.

Омметры выпускают с последовательным (рис. 5.2а) и параллельным (рис. 5.2б) включением измерительного механизма и объекта исследования. При последовательном включении угол поворота подвижной части измерительного механизма

α = , (5.8)

а при параллельном включении

α = , (5.9)

где S_I – чувствительность измерительного механизма к току, R – сопротивление измерительного механизма, R_x – измеряемое сопротивление, R_Д – сопротивление добавочного резистора, необходимого для ограничения тока в параллельной схеме, U – напряжение источника питания. Из выражений (5.8) и (5.9) следует:

1 ) угол поворота подвижной части определяется значением R_x, поэтому шкала прибора может быть проградуирована в единицах измерения сопротивления (омах) при постоянном напряжении источника питания, при этом получаемая шкала при обеих схемах включения неравномерна;

2) так как показания прибора зависят от изменения напряжения питания, то в этих омметрах постоянным поддерживается значение произведения BU = const, а следовательно, и S_IU = const. Это обеспечивается встраиванием в магнитную систему прибора магнитного шунта в виде ферромагнитной пластинки переменного сечения, шунтирующего рабочий воздушный зазор. Перемещая эту пластинку с помощью специальной ручки на панели прибора, можно менять магнитную индукцию B, а значит и чувствительность S_I, компенсируя изменение напряжения источника питания.

Последовательная схема применяется для измерения больших сопротивлений (до сотен мегом), параллельная - для измерения малых (до 1000 Ом). Обычно омметры выполняют в виде переносных приборов классов точности 1,5 и 2,5.

Гальванометры широко применяют в качестве нуль-индикаторов, а также для измерения малых токов, напряжений и количества электричества. Подробнее гальванометры будут рассмотрены ниже.

Эксплуатационные свойства. Основными достоинствами магнитоэлектрических приборов являются равномерная шкала, высокая точность и высокая чувствительность.

Равномерность шкалы связана с независимостью чувствительности к току S_I от угла поворота подвижной части и измеряемой величины. Высокая точность объясняется рядом причин. Наличие равномерной шкалы уменьшает погрешности градуировки и отсчета. Влияние внешних электрических полей отсутствует, а влияние внешних магнитных полей незначительно благодаря сильному собственному магнитному полю в воздушном зазоре (0,2 – 1,2 Тл). По этой же причине приборы имеют малое собственное потребление энергии. В отношении чувствительности магнитоэлектрические приборы не имеют себе равных среди электромеханических приборов. Например, микроамперметр М95 имеет ток полного отклонения 0,1 мкА (при классе точности 1,0). Именно поэтому гальванометры, как приборы, обладающие наибольшей чувствительностью, в подавляющем большинстве бывают только магнитоэлектрическими.

К недостаткам магнитоэлектрических приборов следует отнести возможность непосредственного (без преобразователей) применения для измерения лишь в цепях постоянного тока, сложность конструкции и ее дороговизна (например, по сравнению с электромагнитными приборами), невысокую перегрузочную способность (при перегрузке обычно перегорают токоподводящие пружинки или растяжки), подверженность влиянию температуры. Наиболее неблагоприятным в отношении влияния температуры является амперметр с шунтом. При неизменном токе с повышением температуры сопротивления измерительного механизма и шунта меняются по-разному, вследствие чего происходит перераспределение токов между шунтом и подвижной катушкой. Для компенсации возникающей температурной погрешности применяют схемы термокомпенсации, простейшая из которых показана на рис. 5.3. Здесь уменьшение температурной погрешности достигается за счет включения последовательно с измерительным механизмом сопротивления R_Д из манганина.

Г альванометры. Гальванометром называется прибор с неградуированной шкалой, имеющий высокую чувствительность к току и напряжению. Высокая чувствительность достигается путем уменьшения противодействующего момента и использования светового указателя с большой длиной светового луча.

Конструктивно различают переносные и стационарные гальванометры. Переносные гальванометры имеют встроенную шкалу, в них используются как стрелочные, так и световые указатели. Подвижная часть устанавливается на растяжках. У стационарных гальванометров шкала устанавливается на некотором расстоянии от прибора. Чувствительность при этом зависит от расстояния между зеркальцем гальванометра и шкалой, а постоянная прибора устанавливается для расстояния в 1 м, например, C_I = 1,5×10^-7 А·м/мм. Подвижная часть стационарных гальванометров крепится на подвесе, что требует установки по уровню. Подвод тока к рамке обеспечивается подвесом и безмоментной нитью. Для измерения угла поворота на подвижной части закреплено зеркальце, на которое фокусируется луч света от специального осветителя.

Существуют три разновидности магнитоэлектрических гальванометров:

1) гальванометр постоянного тока – применяется для измерения малых постоянных токов и напряжений, а также в качестве нуль-индикатора в мостах и компенсаторах (потенциометрах) постоянного тока;

2) баллистический гальванометр – предназначен для измерения малых количеств электричества, протекающих в течение коротких промежутков времени;

3) вибрационный гальванометр – используется в качестве нуль-индикатора в мостах и компенсаторах (потенциометрах) переменного тока, а также для построения магнитоэлектрических вибраторов (измерительных механизмов светолучевых осциллографов).

В подавляющем большинстве конструкций гальванометров подвижной частью является рамка с током, и только вибрационный гальванометр может иметь в качестве подвижной части либо постоянный магнит, либо рамку.

Важной характеристикой гальванометра является постоянство нулевого положения указателя, под которым понимают невозвращение указателя к нулевой отметке при плавном его движении от крайней отметки шкалы. По этому параметру гальванометрам присваивают разряд постоянства, который указывают на шкале прибора в виде цифрового обозначения разряда, заключенного в ромб.

Гальванометр должен иметь корректор (для установки указателя на нулевую отметку) и арретир (для фиксации подвижной части в неподвижном положении, например, при переноске). Кроме того, стационарные гальванометры обычно имеют магнитный шунт, регулируя положение которого можно менять чувствительность прибора.

Гальванометры необходимо защищать от помех. Так, от механических сотрясений гальванометры защищают, устанавливая их на капитальные стены или специальные фундаменты; от токов утечки – с помощью заземляемых экранов и т. п.

Теория движения подвижной части гальванометра постоянного тока. Согласно (4.5) уравнение движения подвижной части гальванометра

J + P + W = M_вр .

В этом выражении вращающий момент M_вр = BSwI как для любого магнитоэлектрического прибора (см. выше). Коэффициент успокоения P определяется двумя составляющими

P = P₁ + P₂ ,

где P₁ – коэффициент успокоения вследствие трения рамки о воздух, который в уже изготовленном приборе является постоянной величиной, P₂ – коэффициент магнитоиндукционного успокоения, определяемый из следующих соображений. При повороте рамки от начального положения на угол α магнитный поток Φ, пронизывающий ее контур, изменится, и в обмотке рамки возникнет ЭДС самоиндукции

e = - w = - wBS ,

поскольку в воздушном зазоре, в котором перемещается рамка, создается радиальное магнитное поле с Φ = BSα .

Если рамка замкнута на внешнее сопротивление, то в образовавшейся с обмоткой рамки цепи возникнет электрический ток, равный

i = = - ,

где R_г и R_вн – сопротивления обмотки рамки гальванометра и внешней цепи, на которую она замкнута. В результате взаимодействия этого тока с полем постоянного магнита измерительного механизма возникает момент успокоения

M_{усп 2} = wBSi = - = - P₂ ,

откуда P₂ = . Таким образом, коэффициент магнитоиндукционного успокоения зависит как от сопротивления внешней цепи, так и от конструктивных особенностей магнитоэлектрического измерительного механизма, в частности, от индукции в воздушном зазоре.

Представим уравнение движения подвижной части гальванометра в каноническом виде, разделив все его члены на коэффициент при высшей производной:

+ + α = I . (5.10)

Полученное уравнение является линейным дифференциальным уравнением второго порядка с постоянными коэффициентами и ненулевой правой частью, общее решение которого имеет вид α = α_уст + α_св , где α_уст – установившаяся (или вынужденная) составляющая, являющаяся частным решением уравнения (5.10) и имеющая вид правой части (α_уст = I), α_св – свободная составляющая, являющаяся общим решением соответствующего (5.10) однородного уравнения (с нулевой правой частью) и определяемая видом корней характеристического уравнения

k² + k + = 0 ,

которые в общем виде можно записать как

k₁ = - + , k₂ = - - , (5.11)

где = ω₀ – частота собственных колебаний подвижной части при отсутствии успокоения, = δ – коэффициент затухания. Корни уравнения в зависимости от знака подкоренного выражения могут принимать различные значения, которые определяют вид решения исходного уравнения, а, следовательно, и характер движения подвижной части гальванометра.

Различают три характерных режима работы гальванометра.

1. - > 0 или > 1 или β = > 1 ,

где β – степень успокоения (одна из основных характеристик гальванометра). В этом случае корни характеристического уравнения вещественные и разные. Общее решение уравнения (5.10) имеет вид

α = I + C₁exp(k₁t) + C₂exp(k₂t) , (5.12)

где C₁ и C₂ – постоянные интегрирования, определяемые из начальных условий при t = 0. Так как в начальный момент рамка находится в покое, то начальными условиями будут

α = 0 , = 0 .

Выражение (5.12) не содержит периодических функций, вследствие чего, движение подвижной части гальванометра будет апериодическим (кривая 3 на рис. 5.4). При этом, чем больше коэффициент успокоения P, тем больше будет время достижения конечного равновесного положения.

2. - < 0 или β = < 1 .

В этом случае корни характеристического уравнения будут комплексно-сопряженными, а общее решение уравнения (5.10) будет иметь вид

α = I + C₃exp(-δt) sin (ω^'t + θ) , (5.13)

г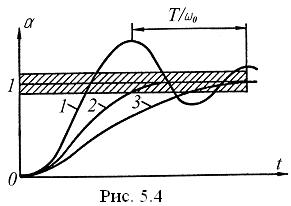 де δ = , ω^' = . Постоянные интегрирования C₃ и θ определяются аналогично С₁ и C₂ . Наличие тригонометрической функции указывает на колебательный характер движения подвижной части гальванометра (с круговой частотой ω^'). Амплитуда колебаний равна коэффициенту C₃exp(-δt) при тригонометрической функции и является затухающей функцией времени (кривая 1 на рис. 5.4). Таким образом, при t = амплитуда станет равной нулю и подвижная часть повернется на конечный угол α = α_уст = I .

3. - = 0 или β = = 1 .

Это пограничный (между апериодическим и колебательным режимами) или критический режим работы гальванометра. При этом корни характеристического уравнения вещественные, равные. Общее решение дифференциального уравнения (5.10) примет вид

α = I + (C₄ + C₅t) exp(-δt) . (5.14)

Постоянные интегрирования C₄ и C₅ определяются также, как и в двух предыдущих случаях. Рассмотренному случаю соответствует кривая 2 на рис. 5.4, т. е. при критическом режиме подвижная часть двигается апериодически, но наиболее ускоренно. Соответствующий суммарный коэффициент успокоения называется коэффициентом критического успокоения P_кр. Его значение можно определить из выражения

= 1 ; P_кр = 2 . (5.15)

С другой стороны, как было показано выше, суммарный коэффициент успокоения

P_кр = P₁ + , (5.16)

где R_вн.кр – внешнее критическое сопротивление гальванометра, которое определяется как наибольшее сопротивление внешней цепи, на которое замкнута катушка гальванометра и при котором подвижная часть во время переходного процесса движется апериодически, но наиболее ускоренно. Сопротивление R_г + R_вн.кр = R_кр называется полным критическим сопротивлением гальванометра. Приравняв выражения (5.15) и (5.16) можно определить R_вн.кр.:

R_вн.кр = . (5.17)

У большинства гальванометров магнитная система снабжена магнитным шунтом, при помощи которого можно изменять индукцию B в рабочем зазоре и, согласно (5.17), критическое сопротивление гальванометра.

Теория движения подвижной части баллистического гальванометра. Баллистическим называется гальванометр, отличающийся увеличенным моментом инерции и предназначенный для измерения количества электричества. Конструктивно баллистический гальванометр отличается от обычного гальванометра постоянного тока наличием дополнительной детали подвижной части в виде цилиндра, которая увеличивает момент инерции подвижной части. Считается, что подвижная часть начинает свое движение после окончания импульса измеряемого тока в обмотке катушки гальванометра. Поэтому необходимо рассмотреть два интервала времени.

Первый интервал 0 t τ_и, где τ_и – длительность импульса тока. Поскольку подвижная часть в течение этого интервала находится в покое, α = 0 и уравнение движения подвижной части

+ + α = i (5.18)

примет вид

+ = i . (5.19)

Интегрируя это уравнение в пределах данного интервала, найдем

+ = ,

а так как α = 0, то получим

= Q ,

где есть количество электричества Q, протекающее через рамку гальванометра за время импульса τ_и. Отсюда получаем, что в конце импульса начальная скорость рамки оказывается пропорциональна протекшему за этот промежуток времени количеству электричества.

Второй интервал времени τ_и t начинается с момента прекращения импульса и начала движения подвижной части. Ток в контуре рамки теперь равен нулю, и правая часть уравнения (5.18) обращается в нуль. Таким образом, движение подвижной части во втором интервале времени будет описываться уравнением

+ + α = 0 . (5.20)

Параметры измерительной системы подбираются такими, чтобы движение подвижной части соответствовало критическому режиму, а для этого режима работы гальванометра решение уравнения (5.20) имеет вид

α = exp(-δt) (C₁ + C₂t) . (5.21)

Постоянные интегрирования С₁ и C₂ определяются из начальных условий при t = τ_и:

α = 0 , = Q . (5.22)

Определить первый наибольший угол поворота подвижной части баллистического гальванометра α_1m можно, взяв от уравнения, полученного из (5.21) с учетом (5.22), первую производную, затем приравнять ее нулю, решить относительно t и подставить полученное значение t в (5.21). Окончательно для α_1m получим

α_1m = ,

где S_Q = – баллистическая чувствительность, определяемая как амплитуда первого отклонения подвижной части гальванометра, выраженная в делениях шкалы, отстоящей от зеркальца на расстоянии 1 м, и получаемая при прохождении через рамку подвижной части количества электричества в 1 Кл. Баллистическая чувствительность зависит от степени успокоения.

Величина, обратная S_Q, носит название постоянной баллистического гальванометра C_Q. Она равна количеству электричества, необходимому для получения α_1m в 1 мм шкалы, отстоящей на расстоянии 1 м от зеркала.

Вибрационный гальванометр представляет собой магнитоэлектрический прибор для измерения переменного тока, подвижная часть которого обладает на столько малым моментом инерции, что успевает следить за изменением измеряемого переменного тока. Применяются две конструкции вибрационных гальванометров. Наиболее распространена конструкция, в которой подвижной частью прибора является закрепленный на растяжках миниатюрный постоянный магнит, помещенный в переменное магнитное поле электромагнита, по обмотке которого протекает измеряемый ток. В результате взаимодействия полей электромагнита и постоянного магнита подвижная часть прибора колеблется с частотой и амплитудой измеряемого тока (в пределах частотного диапазона). Поскольку используется световой указатель, то на шкале создается световая полоса, ширина которой пропорциональна величине тока. Настраивая подвижную часть в резонанс с частотой измеряемого тока, добиваются наибольшей чувствительности. При этом ширина световой полосы на шкале будет максимальной.

Отношение ширины световой полосы к действующему значению тока через катушку прибора при настройке подвижной части в резонанс называется паспортной чувствительностью вибрационного гальванометра. Величина, обратная чувствительности, называется постоянной гальванометра по току C_I и выражается в А/мм. Частотный диапазон вибрационных гальванометров данной конструкции лежит в пределах десятков-сотен герц. Применяются они в качестве нуль-индикаторов в мостовых и компенсационных схемах переменного тока.

Еще меньшим моментом инерции подвижной части обладают осциллографические гальванометры, применяемые в светолучевых осциллографах для регистрации или наблюдения меняющихся во времени сигналов. Осциллографический гальванометр или вибратор состоит из постоянного магнита, между полюсами которого расположена подвижная часть механизма, представляющая собой либо петлю из тонкой металлической ленты, либо обмотку-рамку из нескольких витков, закрепленную на двух металлических растяжках. Растяжки служат также для подведения тока к рамке и создания противодействующего момента. На ленте или рамке закреплено зеркальце, на которое направляется световой луч. Благодаря малому моменту инерции подвижной части осциллографические гальванометры позволяют наблюдать электрические сигналы в частотном диапазоне до 30 кГц.

Магнитоэлектрические логометры. В логометрах противодействующий момент создается электрическим путем. Подвижная часть этих приборов состоит из двух жестко скрепленных между собой рамок с катушками, по которым протекают токи I₁ и I₂. Токи в рамках направлены таким образом, что создаваемые ими моменты действуют навстречу друг другу. Приняв один из моментов вращающим, другой можно считать противодействующим. Хотя бы один из параметров, определяющих значения моментов, должен зависеть от угла поворота подвижной части α. Технически наиболее просто сделать зависящей от угла α магнитную индукцию B. Для этого поле в зазоре должно быть неравномерным, что достигается неравномерностью самого зазора.

В общем виде выражения для моментов M₁ и M₂ в соответствие с (5.4) можно записать следующим образом:

M₁ = B₁(α)S₁w₁I₁; M₂ = B₂(α)S₂w₂I₂ ,

где B₁(α) и B₂(α) – функции, выражающие закон изменения индукции для рамок при их перемещении в зазоре. В равновесии вращающий и противодействующий моменты равны друг другу:

B₁(α)S₁w₁I₁ = B₂(α)S₂w₂I₂ ,

откуда

= .

Выразив отсюда угол поворота α, полученную зависимость можно представить в виде

α = F , (5.23)

т . е. отклонение подвижной части логометра зависит от отношения токов в его обмотках. Отметим, что в логометрах отсутствует механический противодействующий момент, который возвращал бы указатель после измерения на нулевую отметку шкалы.

В настоящее время магнитоэлектрические логометры применяются для измерения больших сопротивлений в приборах, которые называются мегомметрами. Схема включения логометра в мегомметре представлена на рис. 5.5. На этой схеме 1 и 2 – рамки логометра с сопротивлениями R₁ и R₂; R_н и R_д – добавочные резисторы, постоянно включенные в схему; R_x – измеряемое сопротивление; U – напряжение источника питания, в качестве которого применяется магнитоэлектрический генератор с ручным приводом, встроенный в корпус прибора. Так как

I₁ = , I₂ = ,

то на основании формулы (2.28)

α = F , (5.24)

т. е. угол отклонения подвижной части определяется значением R_x и не зависит от напряжения источника питания U. Класс точности современных мегомметров составляет 1,0; 1,5.