Указания к оформлению работы

1. Все расчеты должны быть оформлены аккуратно на бланках отчета по прилагаемой форме. К расчетам прилагаются:

а) бумажный диск с вычерченными на нем зубьями;

б) калька с картиной зацепления.

2. На бумажном диске должны быть указаны фамилии студентов, факультет, курс, группа, дата выполнения работы.

Оформленный отчет и бумажный диск должны быть подписаны преподавателем, руководившим выполнением работы.

Образец бланка представлен в приложении Б.

Контрольные вопросы для защиты лабораторной работы №2

1. Определения: зубчатый механизм, параметры цилиндрического зубчатого колеса: делительная поверхность, шаг, модуль зуба, поверхность вершин, поверхность впадин, боковая главная поверхность, боковая переходная поверхность, основание зуба, ножка зуба, головка зуба, линия зуба, профиль зуба.

2. Основная теорема зацепления. Взаимоогибаемые кривые.

3. Эвольвента: определение, уравнения и свойства эвольвенты.

5. Параметры эвольвентных зубчатых колес и передачи: шаг, модуль, толщина зуба, ширина впадины, высота головки зуба, высота ножки зуба (коэффициент высоты зуба, коэффициент радиального зазора), основная окружность, делительная окружность, начальные окружности, окружность вершин зубьев, окружность впадин зубьев, угол зацепления, угол главного профиля, эвольвентный угол, угол развернутости эвольвенты, межосевое расстояние, передаточное число, теоретический участок линии зацепления, практический участок линии зацепления.

6. Свойства эвольвентного зацепления.

7. В каких случаях назначают смещение инструмента при нарезании зубьев, в чем заключается подрезание зубьев, заострение зубьев. Коэффициент смещения.

8. Как изменяются параметры передачи и зубчатых колес при изготовлении со смещением.

9. Качественные показатели эвольвентного зацепления (перечислить). Дать определение коэффициента перекрытия, угла перекрытия.

Лабораторная работа № 3 кинематический анализ эпициклических зубчатых механизмов

Цель работы: получение и закрепление навыков кинематического расчета эпициклических зубчатых механизмов аналитическим и графоаналитическим методами.

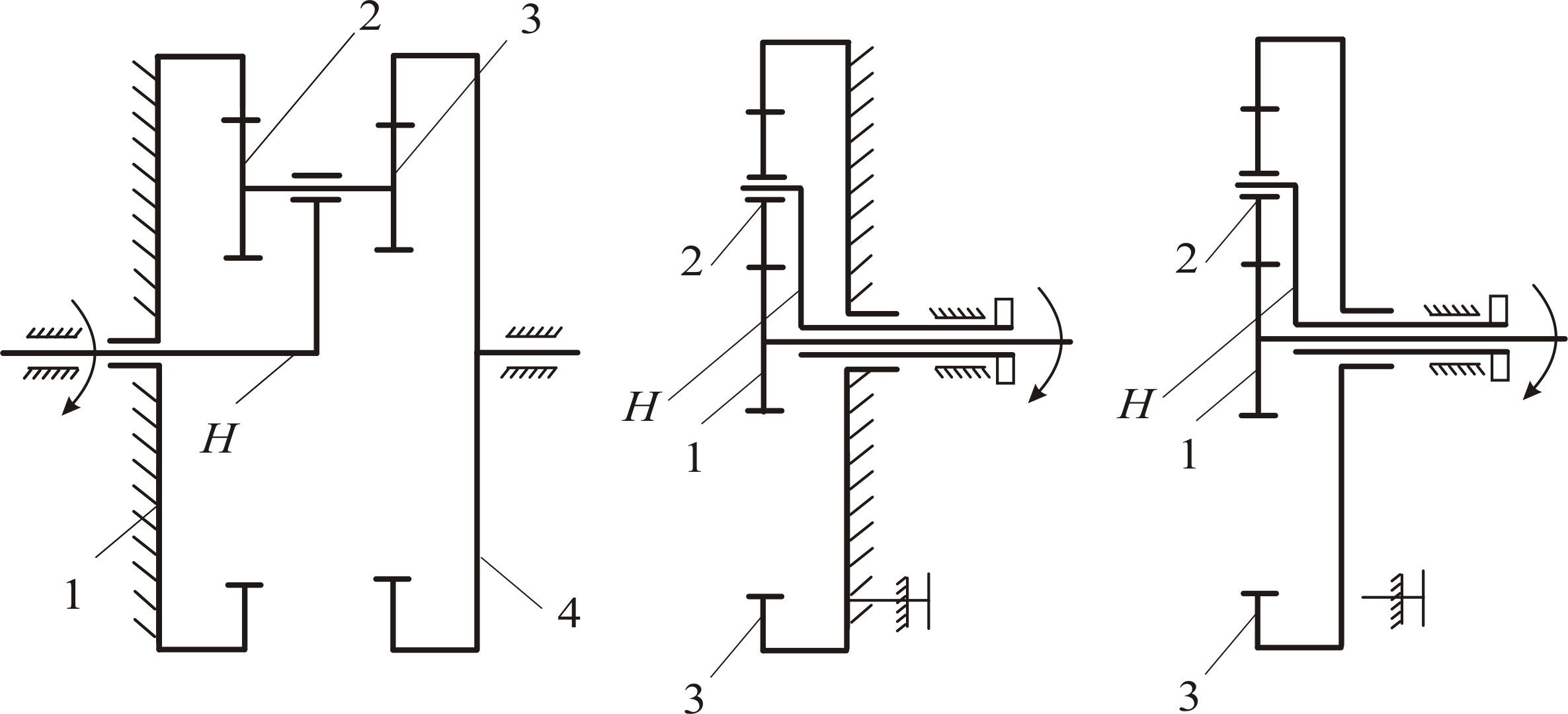
Эпициклическим называют зубчатый механизм, в котором хотя бы одно их зубчатых колес совершает сложное плоское движение. Такие колеса с движущимися геометрическими осями называют сателлитами. Подвижное звено, в котором помещены оси сателлитов, называют водилом. Колеса, по которым обкатываются сателлиты, называют центральными. Если одно их центральных колес неподвижно, механизм называется планетарным, если все центральные колеса подвижны, механизм – дифференциальный. Схемы эпициклических зубчатых механизмов приведены на рис. 21, описание – на стр. 37.

Содержание и порядок выполнения лабораторной работы

1. Вычертить структурную схему механизма по заданному варианту. На схеме обозначить номера зубчатых колес и водило.

2. Из табл. 3. выписать исходные данные для расчета согласно заданному преподавателем варианту – частоты вращения зубчатых колес и водила , мин^-1. Указать также, для каких звеньев (колес, водила) частоты вращения подлежат расчету. Частота вращения звена, вращающегося по ходу часовой стрелки, обозначена со знаком «плюс», вращающегося против хода часовой стрелки – со знаком «минус».

3. Дать характеристику эпициклического механизма: планетарный или дифференциальный, однорядный или двухрядный, с однотипным или разнотипным зацеплением – в случае однотипного указать, какое это зацепление. Если схема включает также простой зубчатый механизм, следует это отметить.

4. Сосчитать числа зубьев колес и занести данные в таблицу (форма табл. 4).

5. Выполнить кинематический расчет механизма аналитическим методом, используя формулу Виллиса. При этом нужно определить неизвестные частоты вращения звеньев (абсолютные и относительные), и передаточное число механизма. Относительные частоты вращения получают путем деления абсолютных частот вращения звеньев на абсолютную частоту вращения входного звена. Результаты расчета оформить в виде таблицы (форма табл. 5).

6. Определить величину модуля зубьев для колес механизма

m, мм. Для этого нужно измерить межосевое расстояние a_W, мм. Используя известные значения чисел зубьев двух сопряженных колес z₁ и z₂, выразим модуль из формулы для вычисления межосевого расстояния:

Таблица 3

Задаваемая величина и направление частоты вращения звеньев

34	Модель механизма	Вариант	Частота и направление вращения колес и водила , мин-1
			1 колесо	2 колесо	3 колесо	3′ колесо	4 колесо	4′ колесо	водило Н
	А	1	0	определяется	определяется	-	определяется	-	+60
		2	0	определяется	определяется	-	+3	-	определяется
		3	0	определяется	определяется	-	+100	-	определяется
		4	0	определяется	определяется	-	определяется	-	+20
	Б	5	+30	определяется	0	-	-	-	определяется
		6	определяется	определяется	0	-	-	-	+20
		7	определяется	определяется	-10	-	-	-	+15
		8	+5	определяется	определяется	-	-	-	-5
	В	9	-5	определяется	+50	-	-	-	определяется
		10	-50	определяется	определяется	определяется	определяется	0	определяется
		11	-50	определяется	определяется	определяется	0	определяется	определяется
		12	-50	определяется	определяется	определяется	определяется	+10	определяется
		13	-50	определяется	определяется	определяется	+5	определяется	определяется
	Примечание: знак «плюс» указывает на направление вращения по ходу часовой стрелки, «минус» - против хода часовой стрелки

– при внешнем зацеплении,

– при внутреннем зацеплении.

При внутреннем зацеплении z₂ – число зубьев колеса с внутренними зубьями.

Модуль отсюда будет равен

или

Следует округлить расчетное значение модуля до ближайшего стандартного m из ряда (ГОСТ 9563–60): 1,0; 1,25; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0; 7,0; 8,0, 9,0; 10,0; 12,0; 16,0 мм и т.д.

7. Выполнить кинематический расчет механизма графоаналитическим методом. Графические построения следует выполнять на отдельном листе. Результаты оформить в виде таблицы (форма табл. 6).

8. Сравнить результаты, полученные аналитическим и графоаналитическим методами. Отличие в результатах, полученных двумя данными методами, выразить в процентах и оформить в виде табл. 7.

Таблица 4

Числа зубьев колес

z1	z2	z3	z3′	z4	z4′

36	а б
	схема А схема Б	схема В

Рис.21. Модели эпициклических механизмов (для схемы Б показаны 2 варианта – а - планетарный и б -дифференциальный)

Таблица 5

Частоты вращения звеньев механизма

Показатель	Водила nH	Колеса 1 n1	Колеса 2 n2	Колеса 3 n3	Колеса 3′ n3′	Колеса 4 n4	Колеса 4′ n4′
Частота вращения абсолютная ni, мин -1
Частота вращения относитель­ная

МОДЕЛИ ЭПИЦИКЛИЧЕСКИХ МЕХАНИЗМОВ

Механизм, выполненный по схеме А (рис. 21) является плане­тарным, так как в нем центральное колесо 1 закреплено и является неподвижным. Входным звеном является водило Н, выходным - колесо 4.

Механизм, выполненный по схеме Б, может быть планетарным или дифференциальным в зависимости от закрепления или освобож­дения центрального колеса 3. Закрепление колеса осуществляется штифтом, смонтированным на станине механизма. Колесо необхо­димо повернуть таким образом, чтобы отверстие на спице колеса совпало с осью штифта. После этого повернуть и установить штифт в глубокой прорези.

При закреплении колеса 3 получаем планетарный механизм с входным центральным колесом 1. Выходное звено – водило Н, ко­лесо 2– сателлит. При освобождении колеса 3 механизм превра­щается в дифференциальный. Входные звенья – колесо 1 и водило Н, выходное звено – колесо 3.

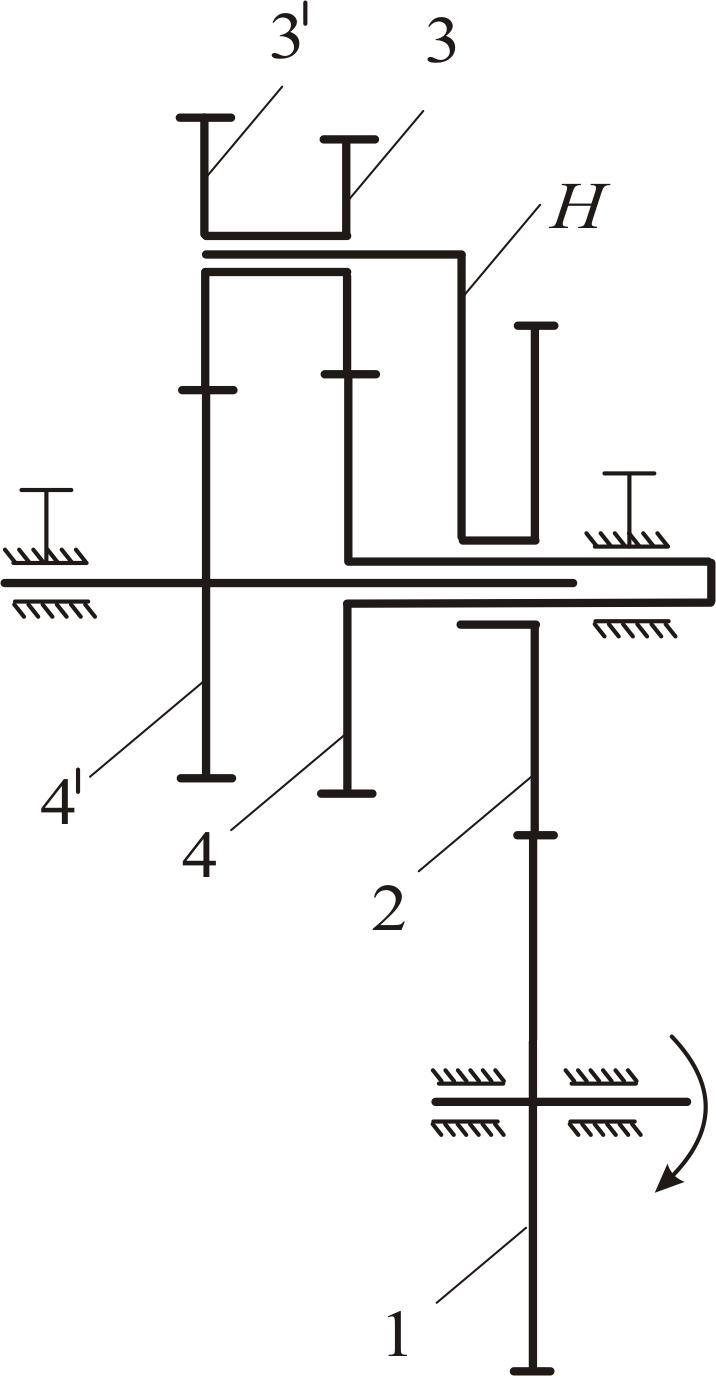
Механизм, выполненный по схеме В, имеет дополнительную внешнюю зубчатую передачу, состоящую из колес 1 и 2. Движе­ние, задаваемое колесу 1, передается колесу 2 и жестко свя­занному с ним водилу Н. Водило при этом является входным звеном эпициклического механизма, в который, наряду с ним, входят сателлиты - колеса 3 и 3′ и центральные колеса 4 и 4'. Эпициклический механизм может быть как планетарным (за­крепляется одно из центральных колес), так и дифференциальным (центральные колеса подвижны). Закрепление колес осуществляется стопорными винтами, которые закрепляют оси правого центрального колеса 4 или левого центрального колеса 4' .

КИНЕМАТИЧЕСКИЙ АНАЛИЗ ЭПИЦИКЛИЧЕСКИХ

МЕХАНИЗМОВ АНАЛИТИЧЕСКИМ МЕТОДОМ

Кинематический анализ эпициклического зубчатого механизма сводится к определению передаточных чисел u, неизвестных частот вращения (n_i, мин^-1) или угловых скорос­тей (ω_i, с^-1) и направлений вращений колес и водила. В качестве ис­ходных данных задаются: кинематическая схема механизма, число и модуль зубьев колес, частоты вращения (угловые скорости) и на­правление вращения входных звеньев.

Входным звеном у планетарного механизма может быть как центральное колесо, так и водило; у дифференциального механиз­ма – два центральных колеса или одно из центральных колес и во­дило.

Аналитический метод основан на применении формулы Виллиса

где – передаточное отношение от входного к выходному колесу при остановленном водиле;

- частота вращения входного звена, мин^-1;

- частота вращения выходного звена, мин^-1;

- частота вращения водила, мин^-1.

Формула Виллиса соответствует обращенному движению механиз­ма, когда всем звеньям сообщается частота вращения, равная по величине час­тоте вращения водила, но в обратную сторону. При этом частота вращения всех звеньев уменьшается на частоту вращения водила, а само водило оказывается условно неподвижным. Эпициклический механизм превращается в зубчатый механизм с неподвижными осями, у которо­го передаточное число может быть найдено через отношения известных чисел зубьев колес. При этом =

При расчете дифференциального механизма неизвестной величи­ной является частота вращения выходного звена или водила . Она легко находится путем преобразования формулы Виллиса. Для определения частоты вращения колес – сателлитов нужно составить уравнение Виллиса для одной из ступеней механизма, сосчитать передаточное число через отношение чисел зубьев и выразить неизвестную частоту вращения сателлита.

Д ля планетарного механизма, в котором центральное колесо j неподвижно, то есть = 0, уравнение Виллиса приобретает вид

где – передаточное число от входного колеса i к выходному

водилу H,

Таким образом, неизвестную частоту вращения водила можно вычислить как:

= или =

Для определения частоты вращения колес-сателлитов нужно составить уравнение Виллиса для одной из ступеней передачи механизма, сосчитать передаточное число через отношение чисел зубьев и решить уравнение Виллиса, выразив неизвестную частоту вращения сателлита.

ПРИМЕР КИНЕМАТИЧЕСКОГО РАСЧЕТА МЕХАНИЗМА АНАЛИТИЧЕСКИМ МЕТОДОМ

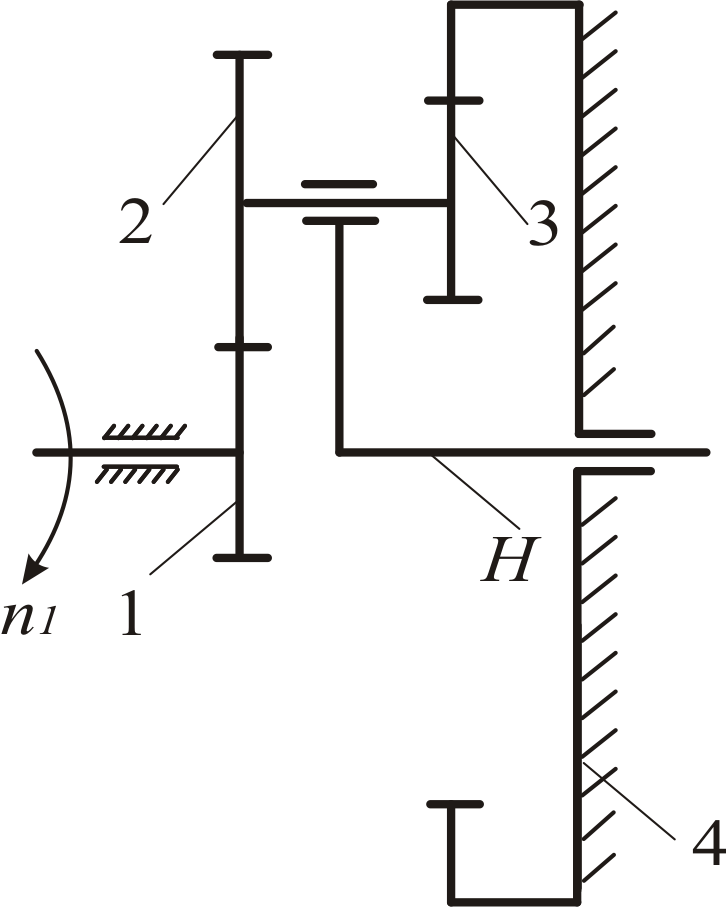
_{Для механизма, схема которого представлена на рис. 22, задана частота вращения центрального колеса 1 – n1, мин-1 и направление его вращения, числа зубьев колес z1, z2, z3 и z4.}

	Данный механизм планетарный (центральное колесо 4 неподвижно, n4 = 0), двухрядный с разнотипным зацеплением. Входным звеном будет колесо 1, выходным – водило Н. Звенья 2 и 3 - сателлиты, расположенные на общей оси вращения. Для нахождения частоты вращения водила составим уравнения Виллиса для обращенного механизма,
Рис. 22

выразив передаточное отношение от первого центрального колеса к четвертому:

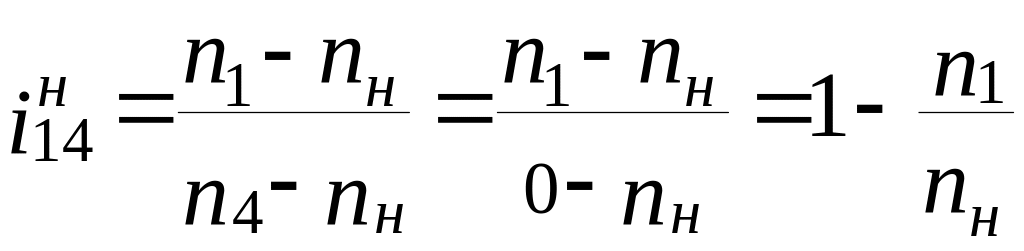, откуда

=

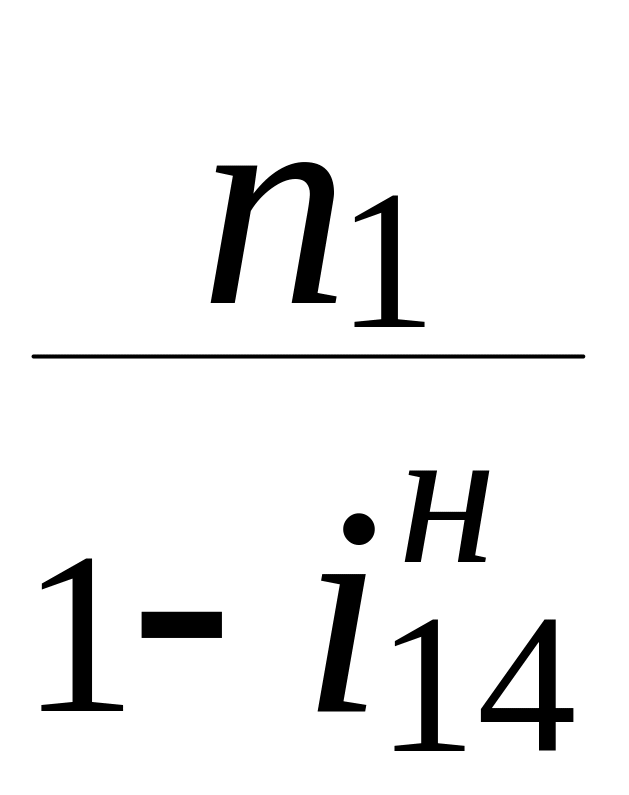
Передаточное число , которое равно передаточному отношению , выразим через отношение чисел зубьев, как для простого двухступенчатого зубчатого механизма:

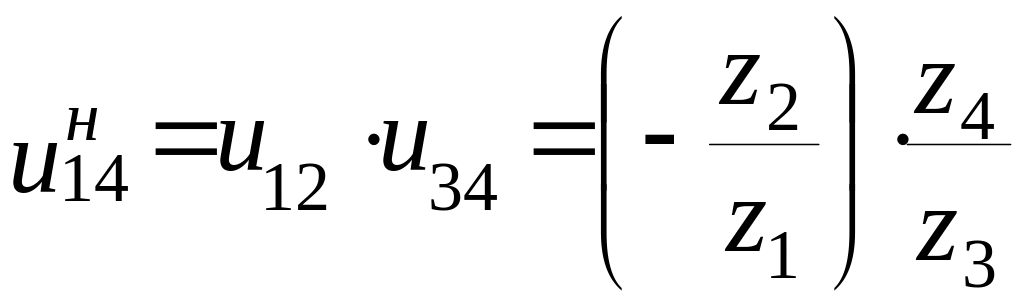
Знак «минус» перед отношением чисел зубьев ставится при внешнем зацеплении, так как направление угловых скоростей при этом противоположно, «плюс» – при внутреннем зацеплении, так как направление вращения сопряженных колес при этом будут одинаковы. Вычислив значение , найдем . Значение в данном случае будет иметь знак «минус», поэтому получится с тем же знаком, что и n₁, а величина n_H будет меньше n₁. Таким образом, данный механизм при передаче движения от первого центрального колеса к водилу уменьшает частоту вращения (является редуктором). Направления вращения входного и выходного звеньев совпадают. Передаточное отношение такого механизма будет

Для вычисления частоты вращения колес - сателлитов составим уравнение Виллиса для одной из ступеней передачи механизма:

Передаточное отношение равно передаточному числу , которое выразим через отношение чисел зубьев, как для простого зубчатого механизма:

Сосчитав передаточное число через отношение чисел зубьев, нужно выразить неизвестную частоту вращения сателлита n₂ из формулы Виллиса при известных величинах n₁ и n_Н.

КИНЕМАТИЧЕСКИЙ АНАЛИЗ ЭПИЦИКЛИЧЕСКИХ

МЕХАНИЗМОВ ГРАФОАНАЛИТИЧЕСКИМ МЕТОДОМ

Графоаналитический метод расчета менее точен, чем аналитический, но обладает наглядностью. Он основан на следующих положениях теоретической механики:

1) линейные скорости точек вращающегося тела пропорцио­нальны угловой скорости (частоте вращения) и радиусу вращения;

2) всякое плоское движение тела эквивалентно повороту его вокруг мгновенного центра вращения;

3) если известны скорости двух точек тела, то можно опре­делить скорость любой третьей точки этого тела.

Графоаналитический метод расчета включает в себя следующие этапы:

1. Построение кинематической схемы механизма.

2. Построение картины линейных скоростей.

3. Построение плана угловых скоростей (частот вращения) и определение неизвестных кинематических параметров.

ПРИМЕР КИНЕМАТИЧЕСКОГО РАСЧЕТА МЕХАНИЗМА ГРАФОАНАЛИТИЧЕСКИМ МЕТОДОМ

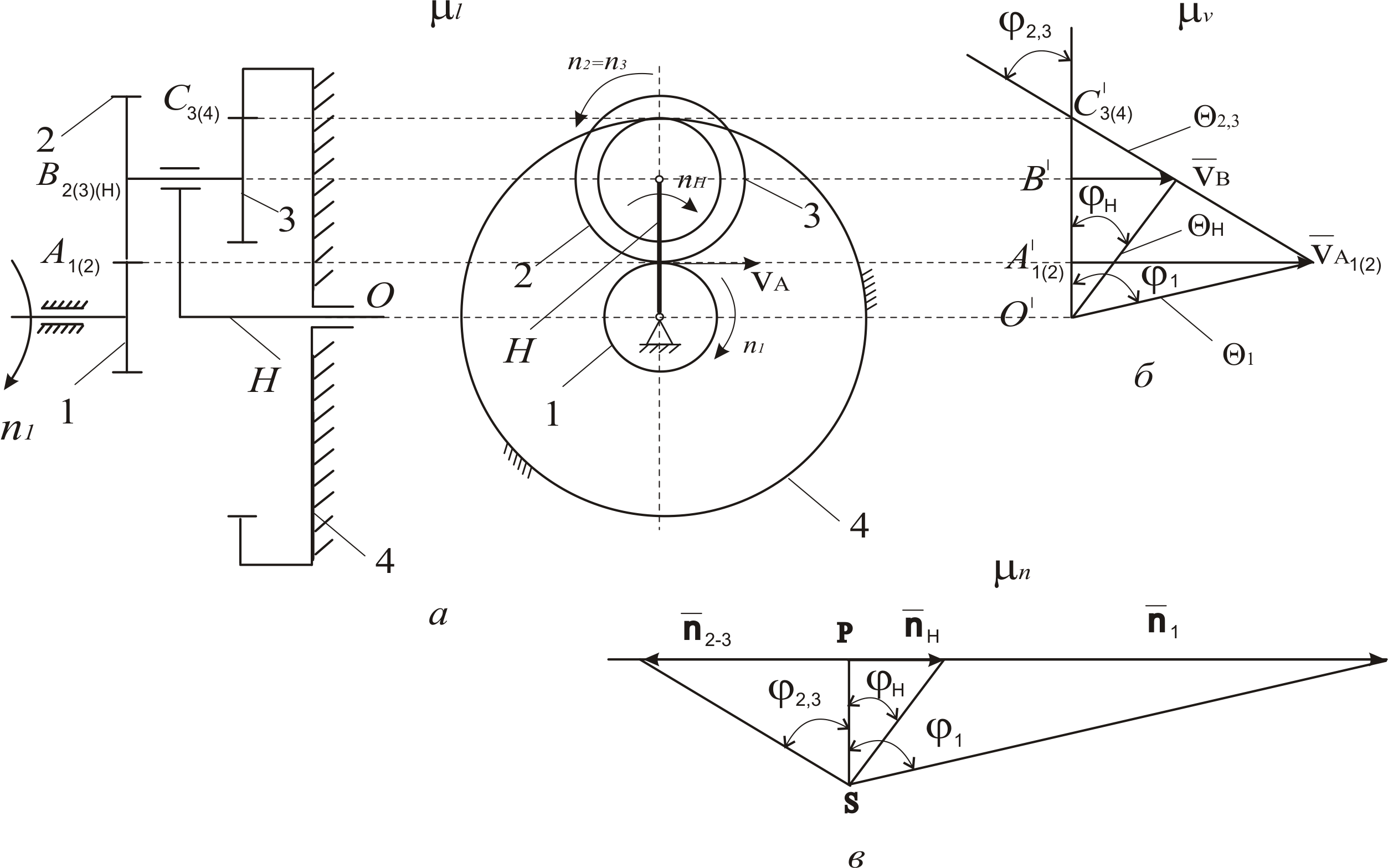
Для расчета воспользуемся схемой механизма, изображенного на рис. 22. Задана частота вращения центрального колеса 1 – n₁, мин^-1 и направление его вращения – по ходу часовой стрелки, числа зубьев колес z₁, z_2, z₃ и z_4. Также известен модуль колес m, мм – одинаковый в обоих рядах зацепления.

Построение кинематической схемы механизма.

1 ). Для построения кинематической схемы нужно вычислить радиусы начальных окружностей зубчатых колес r_W1, мм (полагая, что начальные окружности совпадают с делительными, т.е. r_W1= r₁, r_W2= r₂, r_W3= r₃, r_W4= r₄)_.

2). Выбрать масштабный коэффициент кинематической схемы механизма _l, м/мм:

_l = ,

где r₄ – радиус делительной (начальной) окружности 4 колеса, м;

– отрезок, изображающий размер r₄ на чертеже, мм.

3.) Вычислить длины отрезков, изображающих размеры звеньев на чертеже, мм:

Построить кинематическую схему в выбранном масштабе.

Построение картины линейных скоростей механизма

1). Обозначить на кинематической схеме большими латинскими буквами точки – оси вращения колес и точки зацепления зубьев

(рис. 23, а). Справа от плана механизма провести вертикальную прямую, на которую снести по горизонтали обозначенные точки

(рис. 23, б).

2). Определить линейную скорость точки А₁ для входного звена – центрального колеса 1, м/с:

υ_A1 = ,

где – угловая скорость 1 колеса, с^-1;

– радиус делительной окружности 1 колеса, м;

– частота вращения 1 колеса, мин^-1.

3). Из точки А′₁ на вертикальной прямой отложим вектор линейной скорости точки А₁ произвольной длины . Вектор отложим вправо (вращение звена по ходу часовой стрелки). Линейная скорость точки О, лежащей на оси вращения звена, равна нулю. Проводим прямую, соединив конец вектора скорости точки А₁ и точку О´ на вертикальной прямой (υ_о=0), получая годограф или картину распределения скоростей колеса 1 – θ₁.

4). Вычислим масштабный коэффициент картины линейных скоростей _V, м·с^-1/мм, как отношение величины скорости точки А₁ к длине вектора, изображающего эту скорость на плане:

_V = ,

5). Построим картину распределения скоростей колес 2 и 3 - сателлитов, расположенных на одной оси. Известны скорости двух точек - υ_A1= υ_A2, так как А – точка зацепления 1 и 2 колес, и υ_С3 . Скорость точки υ_С3= υ_С4 = 0, точка С в зацеплении колес 3 и 4 является мгновенным центром вращения колеса 3. Соединим точки на картине линейных скоростей с концом вектора υ_A1(2). Получим годограф скоростей точек колес 2 и 3 – θ_{2, 3}.

6). С помощью годографа θ_{2, 3} находим скорость точки В, расположенной на оси вращения сателлитов 2 и 3 и одновременно принадлежащей водилу Н.

υ_В =_V· ,

где – отрезок, соответствующий скорости точки В на картине

линейных скоростей.

46
	Рис. 23. К кинематическому анализу эпициклического механизма графоаналитическим методом: а – план механизма; б – картина линейных скоростей; в – план частот вращения звеньев.

Ось вращения водила соответствует точке О. Известны линейные скорости двух точек, принадлежащих водилу – точек В (υ_В) и О

(υ_О = 0). Соединив конец вектора υ_В и точку О′, получаем картину распределения скоростей или годограф для водила θ_Н.

Построение плана частот вращения (угловых скоростей) механизма

1). Провести горизонтальную прямую (рис. 23,в), на которой взять точку Р – полюс (из полюса будут направлены векторы, соответствующие частотам вращения звеньев).

2). Из полюса провести перпендикуляр, на произвольном расстоянии от полюса на данном перпендикуляре обозначить точку S. Из точки S провести прямые, параллельные годографам линейных скоростей точек различных звеньев механизма. На горизонтали при этом отсекутся отрезки – векторы частот вращения этих звеньев: соответствующий частоте вращения n₁; соответствующий частоте вращения сателлитов n₂ =n₃; , соответствующий частоте вращения водила n_Н.

3). Определить масштабный коэффициент плана частот вращения звеньев механизма _n, мин^-1/мм:

_n = ,

4). Вычислить частоты вращения звеньев.

n_H = _n · ,

n_2,3 = _n · .

47

5). Определить расхождение между результатами, полученными по аналитическому и графоаналитическому методам расчета, %:

Допустимое расхождение Δ < 3%.

Таблица 6

Кинематический расчет механизма графоаналитическим методом

Величина и расчетная формула в общем виде и с подставленными числовыми значениями	Расчетные величины для звеньев
	1	2	3	3′	4	4′	водило Н
1	2	3	4	5	6	7	8
1.Модуль зубьев, мм
Расчеты
2. Радиусы начальных окружностей колес rWi и длина водила lH, мм
Расчеты
3. Масштаб кинематической схемы механизма l, м/мм
Расчеты
4. Отрезки, изображающие размеры колес и водила на чертеже , мм
Расчеты
5. Линейная скорость точки на начальной окружности входного колеса или оси сателлитов при входном водиле, м/с
Расчеты

Продолжение табл. 6

1	2	3	4	5	6	7	8
6. Отрезок, изображающий линейную скорость точки входного звена, мм
Расчеты
7. Масштаб картины линейных скоростей v, м·с-1/мм
Расчеты
8. Отрезок, изображающий частоту вращения входного звена на картине угловых скоростей (частот вращения), мм
Расчеты
9. Масштаб картины частот вращения звеньев n, мин-1/мм
Расчеты
10. Отрезки, изображающие на картине частот вращения частоты вращения других звеньев, мм
Расчеты
11. Частота вращения звеньев ni, мин-1
Расчеты

Таблица 7

Определение погрешности, полученной

при расчете графоаналитическим методом

Наименование и номер звена	Частота вращения ni, полученная методами		Расчетная формула	Погрешность, %
	аналитическим	графоаналитическим