28.Силы в зацеплении прямозубой конической передачи.

В зацеплении конической передачи действуют силы окружная , радиальная и осевая .

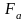По нормали к зубу действует сила , которую раскладывают на и 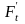. В свою очередь, раскладывается на и . Здесь

,

, ,

,

.

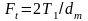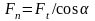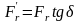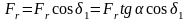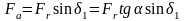Для колеса направление сил противоположно. При этом - радиальная сила, а - осевая.

Приведение прямозубого конического колеса к эквивалентному прямозубому цилиндрическому. Параметры эквивалентных колес ис­пользуют при расчетах на прочность. Форма зуба конического колеса в нормальном сечении дополнительным конусом 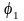такая же, как у цилиндрического прямозубого колеса. Эк­вивалентное цилиндрическое колесо получим как развертку дополнительного конуса, которая ограничена углом 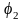. Диаметры эк­вивалентных колес

;

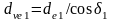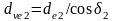
Выражая диаметры через и , запишем 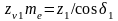или числа зубьев эквивалентных колес

,

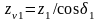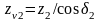
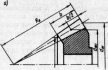
29.Расчет зубьев прямозубой конической передачи по напряжениям изгиба.

Размеры поперечных сечений зуба конического колеса изме­няются пропорционально расстоянию этих сечений от вершины конуса. Все поперечные сечения зуба геометрически подобны. При этом удельная нагрузк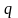а распределяется неравно­мерно по длине зуба. Она изменяется в зависимости от деформации и жесткости зуба в различных сечениях. Можно доказать, что нагрузка распределяется по закону треугольника, вершина которого совпадает с вершиной делительного конуса, и что напряжения изги­ба одинаковы по всей длине зуба.

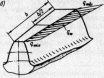
При геометрическом подобии зубьев в различных сечениях их жесткость, как консольных балок, постоянна по всей ширине колеса. Для оценки деформации положим, что зубья колеса 2 абсолютно жесткие, а зубья колеса 1 податливые. При заторможенном колесе 2 нагруженное колесо 1 повернется на угол 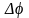вследствие подат­ливости зубьев. Прогиб зубьев в различных сечениях равен 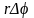, где 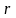- радиус в соответствующем сечении. При постоянной жесткости нагрузка пропорциональна деформациям или в нашем случае ради­усам , которые, в свою очередь, пропорциональны расстояниям от вершины делительного конуса. Если модуль зубьев и нагрузка изменяются одинаково, то напряжения изгиба остаются постоянными по всей длине зуба.

Это позволяет вести расчет по любому из сечений. На практике за расчетное сечение принято среднее сечение зуба с нагрузкой .

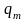По аналогии с прямозубой цилиндрической передачей запишем

,

где для прямозубой передачи 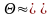0,85 - опытный коэффициент, характеризующий понижение прочности конической прямозубой передачи по сравнению с цилиндрической, - модуль в среднем нормальном сечении зуба.

Коэффициент формы зуба - определяют по графику в соответствии с эквивалентным числом зубьев .

30.Расчет зубьев прямозубой конической передачи по контактным напряжениям.

Для конического зацепления опре­деляют по диаметрам эквивалентных колес. Для среднего сечения зуба получим

.

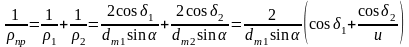Учитывая связь тригонометрических функций и формулу , находим

; .

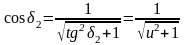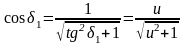После подстановки и несложных преобразований запишем

.

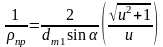На основании формулы можно отметить, что приведенный радиус кривизны в различных сечениях зуба конического колеса изменяется пропорционально диаметрам этих сечений или расстоя­нию от вершины начального конуса. Ранее было сказано, что удель­ная нагрузка также пропорциональна этим расстояниям. Следова­тельно, отношение постоянно для всех сечений зуба. При этом постоянными остаются и контактные напряжения по всей длине зуба, что позволяет производить расчет по любому сечению (в данном случае по среднему). Удельная нагрузка в этом сечении

.

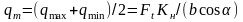Для проверочного расчета прямозубых коничес­ких передач

,

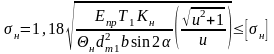где 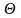=0,85 - опытный коэффициент.

Для проектного расчета последнюю формулу преобразуют. При этом учитывают, что основными габаритными размерами для коничес­ких передач являются 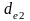и , а нагрузка характеризуется моментом 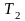на ведомом валу. Вводят эти параметры в формулу и после преобразований получают

,

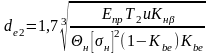где 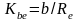коэффициент ширины зубчатого венца относитель­но внешнего конусного расстояния. Рекомендуют 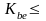0,3. Меньшие значения для неприрабатывающихся материалов (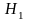 и 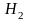> 350 НВ и > 15 м/с).

Наиболее распространено значение 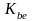= 0,285. При этом

.

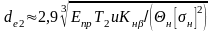Методика выбора коэффициентов, а также определения модуля, числа зубьев и других испол­нительных размеров передачи аналогична методике определения этих параметров для цилиндрических колес.