1.7. Использование переменных

Пример 1.4

Вычислим массу жидкости с плотностью и объемом

8. Система помощи

Окно справки MatLab появляется после выбора опции Help Window в меню Help или нажатием кнопки вопроса на панели инструментов. Эта же операция может быть выполнена при наборе команды helpwin. Для вывода окна справки по отдельным разделам, наберите helpwin topic. Окно справки предоставляет вам такую же информацию, как и команда help, но оконный интерфейс обеспечивает более удобную связь с другими разделами справки. Используя адрес Web-страницы фирмы Math Works, вы можете выйти на сервер фирмы и получить самую последнюю информацию по интересующим вас вопросам. Вы можете ознакомиться с новыми программными продуктами  или найти ответ на возникшие проблемы на странице технической поддержки.

2. Матрицы

2.1. Скаляры, векторы и матрицы

В MatLab можно использовать скаляры, векторы и матрицы. Для ввода скаляра достаточно приписать его значение какой-то переменной, например:

Заметим, что MatLab различает заглавные и прописные буквы, так что p и P — это разные переменные. Для ввода массивов (векторов или матриц) их элементы заключают в квадратные скобки. Так для ввода вектора-строки размером 1×3, используется следующая команда, в которой элементы строки отделяются пробелами или запятыми.

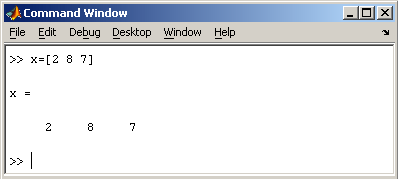
При вводе вектора-столбца элементы разделяют точкой с запятой. Например,

Вводить небольшие по размеру матрицы удобно прямо из командной строки. При вводе матрицу можно рассматривать как вектор-столбец, каждый элемент которого является вектор-строкой.

или матрицу можно трактовать как вектор строку, каждый элемент которой является вектор-столбцом.

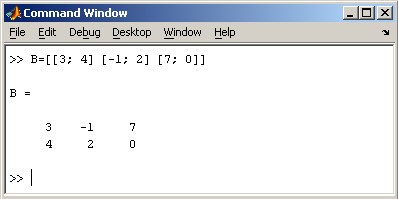
Компоненты вектора могут быть заданы как элементы матрицы, разделенные либо пробелом, либо запятым, и заключенные в квадратные скобки.

Пример 1.5

Вектор скорости в декартовой системе координат имеет вид . Пусть заданы 2 вектора , Вычислим вектор

Мы получили вектор Разность векторов вычисляется анологично.

Пример 1.6

Вычислим скалярное произведение из предыдущего примера.

Примечание: Команда не выполнена. Система выдает ошибку о несогласованности размерностей перемножаемых матриц, т.к. по правилу умножения матриц элементы строки первой матрицы умножаются на элементы первого столбца второй, и их сумма присваивается первому элементу результирующей матрицы и т.д. Для выполнения этого правила нужно транспонировать вторую матрицу. Операция транспонирования выполняется с помощью символа " ' ":

Пример 1.7

Вычислим модуль вектора скорости из примера 1.5 по формуле

Аналогичный результат получается с помощью команды norm вычисления нормы вектора:

Ответ легко проверить

Матрицы можно также перемножать поэлементно.

Пример 1.8

Вычислим результат поэлементного умножения, деления, сложения и вычитания матриц a и b. Точка после переменной является признаком поэлементного умножения.

Количество команд и операций, выполняемых в режиме калькулятора достаточно велико. Рассмотрим некоторые из них.

Пример 1.9

Пусть известны округленные среднесуточные значения температуры воздуха в течение недели Эти данные заданы в виде матрицы t.

Определим минимальную температуру:

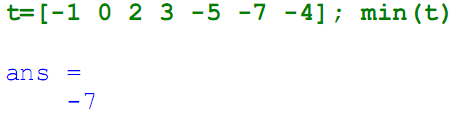
Определим максимальную температуру:

Определим среднюю температуру:

Пример 1.10

Проверим полученное значение средней температуры, воспользовавшись определением средней величины – отношение суммы элементов матрицы к их числу:

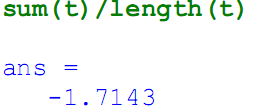
Пример 1.11

Расположим элементы матрицы t по возрастанию или убыванию:

Пример 1.12

Найдем корни системы линейных алгебраических уравнений: