
- •Тема 1. Обыкновенные дифференциальные уравнения.
- •Тема 2. Кратные и криволинейные интегралы
- •Тема 3. Числовые и функциональные ряды.
- •Тема 4. Теория вероятностей.
- •Тема 5. Элементы теории функции комплексной переменной.
- •Тема 6. Элементы операционного исчисления.
- •Свойства преобразования Лапласа
- •Тема 7. Основные уравнения математической физики.
- •Тема 8. Математическая статистика
- •Тема 9. Математическое программирование.
Тема 5. Элементы теории функции комплексной переменной.
Знать определение функции комплексной переменной и уметь ее геометрически изображать.
Уметь находить действительную и мнимую части функции комплексной переменной.
Знать определение предела функции комплексной переменной и уметь их вычислять.
Знать определение функции непрерывной в точке.
Знать определение производной функции комплексной переменной.
Знать условия дифференцируемости функции комплексной переменной (условия Коши-Римана).
Уметь находить производную функции комплексной переменной.
Задания для самостоятельного выполнения
1
Дана функция
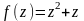 .
Найти значения функции при: а)
.
Найти значения функции при: а)
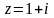 ,
,
б)
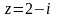 ,
в)
,
в)
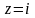 ,
г)
,
г)
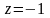 .
.
2
Определить
действительную и мнимую части функции
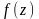 :
:
а)
 ,
б)
,
б)
 ,
в)
,
в)
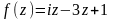 .
.
3 Найдите пределы:
а)
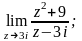
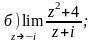
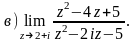
4 Показать, что функция f(z) дифференцируема и найти ее производную.
а)
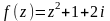 ;
б)
;
б)
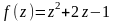 ;
;
в)
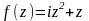 ;
г)
;
г)
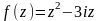 .
.
Образцы решения заданий.
Задание
1.Дана
функция
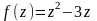 .
Найти значения функции при
.
Найти значения функции при
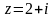 .
.
Решение. Имеем
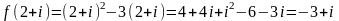 .
.
Задание
2. Определить
действительную и мнимую части функции
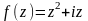 .
.
Решение.
Определим
действительную и мнимую часть функции
,
т.е. представим функцию
в виде
 .
.
Так
как
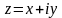 ,
то
,
то
= (x + iy)2 +3i(x + iy) = =
=
=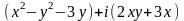 .
.
Следовательно,
u(x,y) = x2 – y2 - 3y; v(x,y) = 2xy + 3x.
Задание
3.
Найдите предел
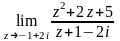
Решение.
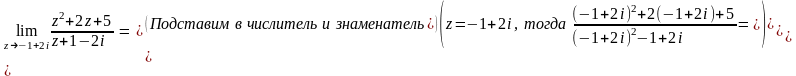
Пусть
функция
 определена
в некоторой области
определена
в некоторой области
 комплексного переменного
комплексного переменного
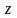 .Пусть
точки
и
.Пусть
точки
и
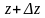 принадлежат
области
.
Приращение функции w
в
точке z:
принадлежат
области
.
Приращение функции w
в
точке z:
 ,
где
,
где
 .
.
Производной
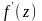
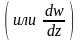 функции
в точке
функции
в точке
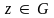 называется предел отношения
называется предел отношения
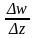 при
при
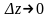
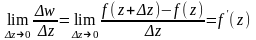 ,
,
если он существует и конечен.
Если существует производная , то функция называется дифференцируемой точке z.
Пусть
,
тогда
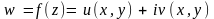 и в каждой точке дифференцируемости
функции
выполняются соотношения:
и в каждой точке дифференцируемости
функции
выполняются соотношения:
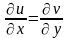 ,
,
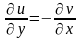 .
.
Эти соотношения называются условиями Коши-Римана.
Обратно,
если в некоторой точке
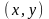 выполняются условия Коши-Римана и, кроме
того, функции
выполняются условия Коши-Римана и, кроме
того, функции
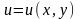 и
и
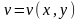 дифференцируемы
как функции двух действительных
переменных, то функция
дифференцируемы
как функции двух действительных
переменных, то функция
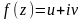 является дифференцируемой в точке, как
функция комплексного переменного
.
является дифференцируемой в точке, как
функция комплексного переменного
.
Задание 4. Показать, что функция f(z) = iz3 + z2 – 3iz дифференцируема.
Решение. Определим действительную и мнимую часть функции f(z) = iz3 + z2 – 3iz , т.е. представим функцию в виде .
Так как , то
f(z) = iz3 + z2 – 3iz = i(x + iy)3 + (x + iy)2 – 3i(x + iy) =
= i(x3 + 3x2yi – 3xy2 – y3i) + x2 + 2xyi – y2 – 3xi + 3y =
= x3i – 3x2y – 3xy2i + y3 + x2 + 2xyi –y2 – 3xi + 3y =
= (y3 + x2 – y2 – 3x2y + 3y) + i(x3 – 3xy2 + 2xy – 3x).
Следовательно,
u(x,y) = y3 + x2 – y2 – 3x2y + 3y; v(x,y) = x3 – 3xy2 + 2xy – 3x.
Проверим выполнение условий Коши–Римана:
, .
Найдем частные производные функций u(x,y) и v(x,y):
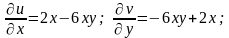
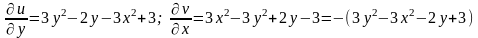 .
.
Условия Коши-Римана выполняются при всех значениях х и у, следовательно, функция f(z) = iz3 + z2 – 3iz является дифференцируемой на всей комплексной плоскости.
Тема 6. Элементы операционного исчисления.
Знать определения оригинала и изображения. Изображения некоторых функций.
Используя таблицу основных формул соответствия и теоремы операционного исчисления, уметь находить изображения оригиналов и оригиналы по их изображениям.
Уметь находить изображения дифференциального выражения.
Уметь находить операционным методом частные решения дифференциальных уравнений с постоянными коэффициентами.
Задания для самостоятельного выполнения
1 Найти изображение F(p) по заданному оригиналу f(t):
а)
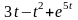 ;
б)
;
б)
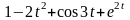 ;
в)
;
в)
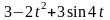 .
.
2 Найти оригинал f(t) по изображению F(p):
а)
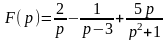 ;
б)
;
б)
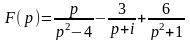 ;
;
в)
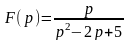 .
.
3 Найти изображение дифференциального выражения:
а)
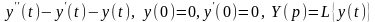 ;
;
б)
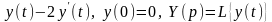 ;
;
в)
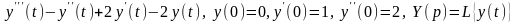 .
.
4 Операционным методом найти решение дифференциального уравнения, удовлетворяющего заданным начальным условиям.
а)
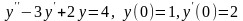 ;
б)
;
б)
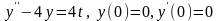 .
.
Образцы решения заданий
Любая комплексная функция f (t) действительного переменного t называется оригиналом, если она удовлетворяет следующим условиям:
1) f (t) – кусочно–непрерывная при t ≥ 0, это значит, что она либо непрерывна, либо в каждом конечном интервале имеет лишь конечное число точек разрыва 1-го рода;
2) f (t) ≡ 0 при t < 0;
3) при t → ∞ функция f (t) растёт не быстрее некоторой показательной функции (имеет ограниченную степень роста), т.е. существует такое положительное число М и такое неотрицательное число s, что для всех t ≥ 0 выполняется неравенство: | f (t) | ≤ M∙est, М > 0, s ≥ 0.
Точная
нижняя грань s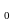
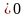 тех значений
s,
для которых выполняется указанное
условие, называется показателем
роста
функции f(t).
тех значений
s,
для которых выполняется указанное
условие, называется показателем
роста
функции f(t).
Изображением
функции f(t)
по Лапласу
называется функция F(p)
комплексного переменного p=s+i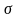 из
некоторой области D
плоскости
комплексного переменного p,
определяемая равенством
из
некоторой области D
плоскости
комплексного переменного p,
определяемая равенством
F(p)=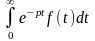 .
.
Связь между функциями f(t) и F(p) будем обозначать в дальнейшем следующим образом: f(t) = L–1{F(p)} или F(p) = L{f(t)}.
Первую запись следует читать так: «Оригинал f (t) имеет изображение F (p)». Вторую запись следует читать так: «Изображение F (p) имеет оригинал f (t)» или «f (t) является оригиналом изображения F (p)». Используются также и другие обозначения.
