Лабораторна робота №10

Розв’язування нелінійних рівнянь

Завдання. Розв’язати рівняння методом:

1. половинного ділення ( бісекцій);

2. простих ітерацій;

3. Ньютона-Рафсона;

4. хорд

(згідно варіанту завдання)

В загальному випадку нелінійне рівняння записують так:

, (1)

 – довільна функція однієї змінної. Вважається, що функція визначається алгебраїчним виразом.

Розв’язування нелінійного рівняння (1) чисельними методами складається з двох етапів:

1. відокремлення коренів;

2. уточнення коренів до заданої точності.

1. Відокремлення коренів

Відокремити корінь означає вказати відрізок , на якому він знаходиться і на якому він єдиний. Такий відрізок називається відрізком відокремлення кореня. Для того, щоб відрізок був відрізком відокремлення кореня необхідно виконання трьох умов Больцано-Коші.

• 1 умова. Функція на кінцях відрізку повинна мати значення різних знаків, тобто .

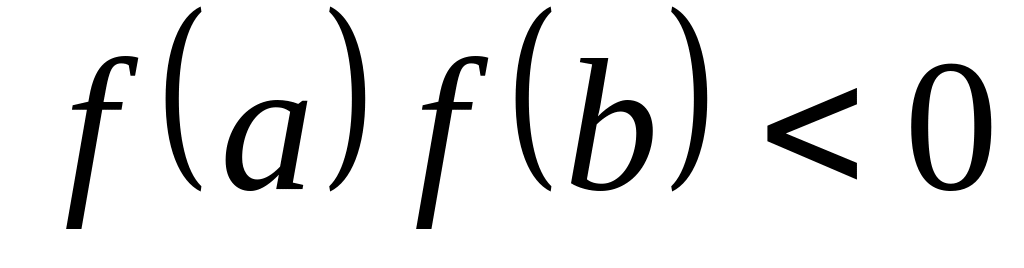• 2 умова. Функція на відрізку має бути неперервною.

• 3 умова. Похідна 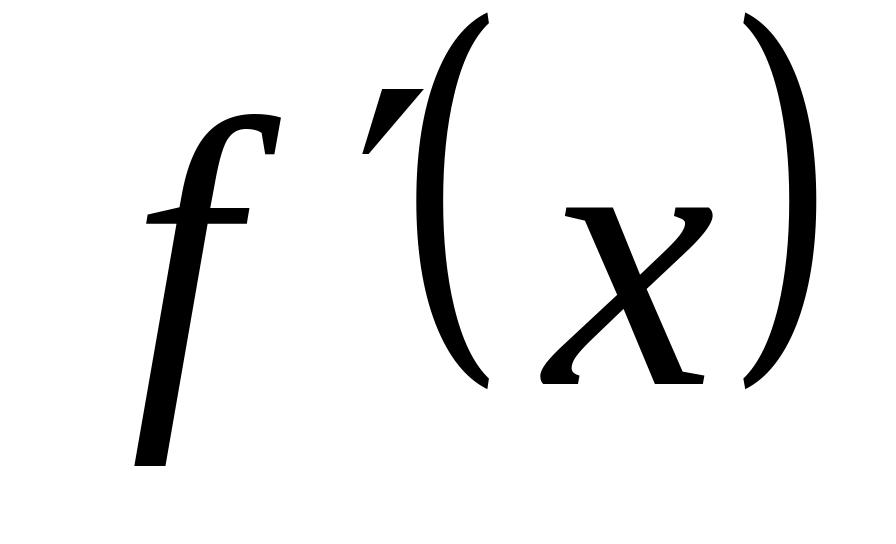не повинна змінювати свого знаку на відрізку . Це означає, що функція на цьому відрізку не повинна мати точок екстремуму.

Відрізок відокремлення кореня можна знайти, якщо побудувати таблицю значень функції за такою програмою.

program vidokremlennya;

var

a, b, h, x: real; {a,b – границі відрізка, на якому досліджується фінкція f(x), h - крок зміни значень аргументу x}

ix, nx: integer; {nx+1 – кількість точок в яких обчислюється значення функції, ix – номер точки x}

function f(x: real): real;

begin

f:=<вираз для функції>;

end;

begin

write (‘a=’); readln (a); write (‘b=’); readln (B); write (‘h=’); readln (h);

writeln(‘ x f(x)’);

nx:=round((B-A)/h)+1;

for ix:=0 to nx do begin x:=a+ixh; writeln (‘x=’, x:1:1, ‘ f(x)=’, f(x):1:2); end;

end.

Приклад. Для функції програма vidokremlennya дає таблицю значень

a=-5

b=5

h=1

x f(x)

-5.0 -5.28

-4.0 -3.35

-3.0 -2.01

-2.0 -1.58

-1.0 -1.54

0.0 -1.00

1.0 0.46

2.0 2.41

3.0 3.99

4.0 4.65

5.0 4.72

Функція змінює знак на відрізку Дослідження поведінки функції на цьому відрізку за допомогою програми vidokremlennya при меншому кроці показали, що вона змінює знак на відрізку лише один раз. Тому цей відрізок можна вибрати відрізком відокремлення. При виборі кроку зміни аргументу необхідно бути обережним. Він має бути не великим, щоб функція не змінювала знаку парну кількість разів.

2. Уточнення коренів нелінійних рівнянь

Уточнення коренів нелінійних рівнянь здійснюється ітераційними методами. В таких методах корінь рівняння шукається як границя послідовних наближень:

,

де називають k-м наближенням (k – наближенням) до кореня рівняння.

Уточнити корінь означає знайти послідовне наближення кореня із заданою наперед абсолютною похибкою , тобто знайти послідовне наближення , яке б задовольняло б нерівності

Для цього використовуються різні ітераційні методи: половинного ділення (бісекцій), Ньютона-Рафсона (дотичних), простих ітерацій, хорд, різні комбіновані методи.

2.1. Метод половинного ділення (метод бісекцій)

Послідовні наближення в методі половинного ділення обчислюються за ітераційною формулою

, (1)

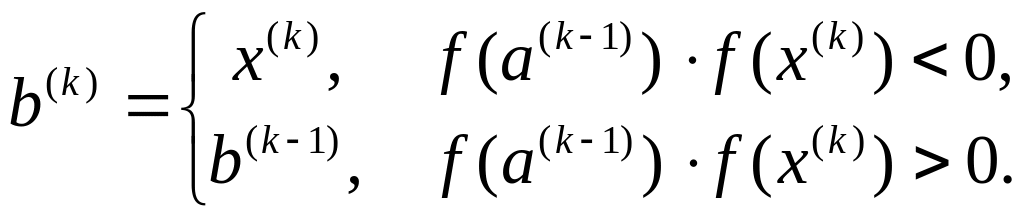
, ,  – відрізок відокремлення.

Очевидно, що похибка наближення

.

З останньої рівності випливає умова закінчення ітераційного процесу

,

де  - параметр, що характеризує точність наближеного кореня. В методі половинного ділення .

Легко підрахувати, що кількість ітерацій необхідних для досягнення точності:

.

З цієї формули випливає, що для одержання кожних трьох вірних десяткових знаків кореня необхідно біля 10 ітерацій. Тобто швидкість методу (кількість необхідних ітерацій) половинного ділення невелика (кількість ітерацій велика).

Алгоритм уточнення кореня нелінійного рівняння реалізований в такій процедурі.

procedure bisect(a,b,eps:real;var x:real;var error:byte);

{Процедура уточнює корінь нелінійного рівнянь методом половинного ділення.

Вхідні дані:

a,b – границі відрізка відокремлення коренів;

eps – параметр, що характеризує точність обчислення кореня рівняння. В методі половинного ділення eps дорівнює абсолютній похибці кореня

Вихідні дані:

x – уточнений корінь на разі успішної роботи процедури;

error – –код помилки. Дозволяє встановити причину неуспішної роботи процедури. Може приймати значення

0 – корінь успішно уточнений;

1 – порушується умова a<b;

2 – на кінцях відрізку відокремлення функція має значення однакового знаку (порушується перша умова Больцано-Коші)}

var

fa,fb,fx:real;

begin

{Перевірка умови a<b}

if a>=b then begin error:=1; exit; end;

{Обчислення значень функції на границях відрізку відокремлення}

fa:=f(a); fb:=f(b);

error:=0;

{Якщо значення функції f(x) на границях відрізку відокремлення одного знаку, то вихід з процедури}

if fa*fb>0 then begin error:=2; exit; end;

{Виконання ітерацій}

while (b-a) > eps do

begin

x:=0.5*(a+b); fx:=f(x);

if fx*fa<0 then begin b:=x; fb:=fx; end

else begin a:=x; fa:=fx; end;

end;

end;

Процедура bisect звертається до функції, яка обчислює значення функції f(x) в довільній точці. В нашому випадку до функції

function f(x:real):real;

begin

f:=x-cosx;

end;