
Лабораторна робота №7
Матрична алгебра
Завдання: Обчислити евклідову норму вектора
![]()
(матриці позначаються великими буквами латинського алфавіту, вектори - грецького алфавіту).
1 Процедури та функції матричної алгебри
До задач матричної алгебри належать операції над багатовимірними векторами, матрицями, тощо. При виконанні дій матричної алгебри необхідно визначити типи даних для представлення векторів, матриць, і т.
const
nmax=10;
type
size=1..nmax;
vector=array[size] of real;
matrix=array[size,size] of real;
1.1. Додавання векторів
Якщо
![]() ,
,![]() то
то
![]() ,
,
,
,
![]() –
істинний розмір векторів.
–
істинний розмір векторів.
procedure add_vector(x,y:vector;n:size;var z:vector);
var
i:size;
begin
for i:=1 to n do z[i]:=x[i]+y[i];
end;
1.2. Віднімання векторів
Якщо
![]() ,
то
,
то
![]() ,
.
,
.
procedure sub_vector(x,y:vector;n:size;var z:vector);
var
i:size;
begin
for i:=1 to n do z[i]:=x[i]-y[i];
end;
1.3. Множення вектора на число
Якщо
![]() ,
то
,
то
![]() ,
,
p – дійсне
число.
,
,
p – дійсне
число.
procedure mult_number_vector(p:real;x:vector;n:size;
var z:vector);
var
i:size;
begin
for i:=1 to n do z[i]:=p*x[i];
end;
7.1.4. Евклідова норма вектора
Евклідовою нормою вектора називають число
![]() .
.
function evklid_norma_vector(x:vector;n:size):real;
var
s:real;
i:size;
begin
s:=0;
for i:=1 to n do s:=s+x[i]*x[i];
evklid_norma_vector:=sqrt(s);
end;
1.5. Норма
вектора
![]()
function norma1_vector(x:vector;n:size):real;
var
s:real;
i:size;
begin
s:=0;
for i:=1 to n do s:=s+abs(x[i]);
norma1_vector:=s;
end;
1.6. Норма
вектора
![]()
function norma2_vector(x:vector;n:size):real;
var
max:real;
i:size;
begin
max:=abs(x[1]);
for i:=2 to n do if abs(x[i])>max then max:=abs(x[i]);
norma2_vector:=max;
end;
1.7. Скалярний добуток векторів
Скалярний
добуток векторів
![]() і
і
![]() обчислюється
за формулою
обчислюється
за формулою
![]()
function scal_mult_vector(x,y:vector;n:size):real;
var
s:real;
i:size;
begin
s:=0;
for i:=1 to n do s:=s+x[i]*y[i];
scal_mult_vector:=s;
end;
1.8. Додавання квадратних матриць
Якщо
![]() ,
то
,
то
![]() ,
,![]() .
.
procedure add_matrix(a,b:matrix;n:size;var c:matrix);
var
i,j:size;
begin
for i:=1 to n do
for j:=1 to n do c[i,j]:=a[i,j]+b[i,j];
end;
1.9. Віднімання квадратних матриць
Якщо
![]() ,
то
,
то
![]() ,
.
,
.
procedure sub_matrix(a,b:matrix;n:size;var c:matrix);
var
i,j:size;
begin
for i:=1 to n do
for j:=1 to n do c[i,j]:=a[i,j]-b[i,j];
end;
1.10. Множення квадратних матриць
Якщо
![]() ,
то
,
то
![]() ,
.
,
.
procedure mult_matrix(a,b:matrix;n:size;var c:matrix);
var
i,j,k:size;
s:real;
begin
for i:=1 to n do
for j:=1 to n do
begin
s:=0;
for k:=1 to n do s:=s+a[i,k]*b[k,j];
c[i,j]:=s;
end;
end;
1.11. Множення квадратних матриць на число
Якщо
![]() ,
то
,
то
![]() .
.
procedure mult_number_matrix(p:real;a:matrix;n:size;
var c:matrix);
var
I,j:size;
begin
for i:=1 to n do
for j:=1 to n do c[i,j]:=p*a[i,j];
end;
1.12. Множення квадратної матриці на вектор
Якщо
![]() ,
то
,
то
![]() ,
.
,
.
procedure mult_matrix_vector(a:matrix;x:vector;n:size;var z:vector);
var
i,k:size;
s:real;
begin
for i:=1 to n do
begin
s:=0;
for k:=1 to n do s:=s+a[i,k]*x[k];
z[i]:=s;
end;
end;
1.13. Транспонування квадратної матриці
Якщо
![]() ,
то
,
то
![]() ,
.
,
.
procedure transp_matrix(a:matrix;n:size;var c:matrix);
var
i,j:size;
begin
for i:=1 to n do
for j:=1 to n do c[i,j]:=a[j,i];
end;
1.14. Евклідова норма квадратної матриці
Евклідовою нормою матриці називають число
![]() .
.
function evklid_norma_matrix(a:matrix;n:size):real;
var
i,j:size;
s:real;
begin
s:=0;
for i:=1 to n do
for j:=1 to n do s:=s+a[i,j]*a[i,j];
evklid_norma_matrix:=sqrt(s);
end;
1.15. Норма
квадратної матриці
function norma1_matrix(a:matrix;n:size):real;
var
i,j:size;
s:vector;
max:real;
begin
for j:=1 to n do
begin
s[j]:=0;
for i:=1 to n do s[j]:=s[j]+abs(a[i,j]);
end;
max:=s[1];
for j:=2 to n do if s[j]>max then max:=s[j];
norma1_matrix:=max;
end;
1.15. Норма квадратної матриці
function norma2_matrix(a:matrix;n:size):real;
var
i,j:size;
s:vector;
max:real;
begin
for i:=1 to n do
begin
s[i]:=0;
for j:=1 to n do s[i]:=s[i]+abs(a[i,j]);
end;
max:=s[1];
for i:=2 to n do if s[i]>max then max:=s[i];
norma2_matrix:=max;
end;
2. Текстові файли
При розв’язуванні задач матричної алгебри необхідно вводити та виводити великі обсяги чисел – значень елементів векторів, матриць тощо. В цьому випадку вводити дані з клавіатури, та виводити їх на екран монітора недоцільно.
Тому дані під час виконання програми зчитують з файлу на диску і записують результат роботи у файл на диску.
Система Turbo Pascal підтримує типізовані, бінарні та текстові файли. Для розв’язування математичних задач , коли необхідно вводити значення даних різних типів в впереміжку, найбільш зручними є текстові файли.
Текстовий файл – це послідовність символів (ASCII-кодів) розділених на рядки керуючими символами: повернення каретки enter (ASCII-код 13) та кінцем рядка eol (ASCII-код 10). Текстові файли завершуються символом eof (ASCII-код 26) Керуючі символи програмою відображення файлу на екрані не відображаються.
Приклад. Текстовий файл
112 114 111 103 114 97 109 32 111 115 116 59 13 10 98 101 103 105 110 13 10 32 32 32 119 105 116 101 108 110 40 39 68 121 110 97 109 111 39 41 32 101 110 100 46 26
відобразиться на екрані так:

В ТР-програмі текстові файли представляються даними файлового типу text – файловими змінними:
var
список файлових змінних:text;
Для зв’язування файлової змінної із файлом на диску, можна скористатися стандартною процедурою
assign(файлова змінна, ім’я файлу);
Якщо в імені файлу маршрут не вказується, то файл шукається в поточному католозі.
Приклад.
var
fin:text;
begin
assign(fin,’lab7.in’);
. . . . . . . . . . . . . . . .
end.
Для зчитування (запису) у файл (з файла) його необхідно відкрити. Це можна зробити за допомогою стандартних процедур
reset (файлова змінна);
або
rewrite(файлова змінна);
Процедура reset перевіряє наявність файлу на диску, на який вказує файлова змінна. Якщо файл існує, то він відкривається для зчитування/запису. Якщо файл не знайдений, то видається повідомлення: ‘File not found’ з припиненням виконання програми.
Процедура rewrite спочатку перевіряє наявність файлу на диску. Якщо той існує, то він знищується, після чого створюється новий порожній файл з тим самим іменем і відкривається для зчитування/запису. Якщо файл не існує, то він створюється і відкривається для зчитування/запису. При відкритті файлу вказівник на символ у файлі встановлюється на перший символ (вказівник – це змінна, яка набуває значення номера символу в текстовому файлі; користувачу вона не доступна)
Якщо необхідно дописати у існуючий файл на диску дані, то можна скористатися стандартною процедурою
append (файлова змінна);
Для зчитування даних із файлу можна скористатися стандартними процедурами
read([файлова змінна,] список введення);
readln([файлова змінна,] список введення);
Якщо файлова змінна не вказується, то здійснюються введення з клавіатури.
Робота процедур read та readln ілюстрюється прикладами
Приклад 1.
var
a:string[5];
b:char;
i,j:integer;
p:real;
fin:text
begin
assign(fin,’proba1.in’);
reset(fin);
read(fin,a,b,i,j,p);
. . . . . . . . . . . . . . .
end.
а) файл proba1.in:
a b c d e f #32 #32 5 #32 #32 2 4 #32 #32 #32 7 . 5 #26
(для зручності замість ASCII – кодів пишуться самі символи, за виключенням символу “пропуск” (код 32) та керуючих символів enter (код 13), eol (код 10), eof (код 26)). На екрані файл зображається одним рядком






Після відкриття файлу, вказівник вказує на перший символ. Це зображається рискою підкреслювання та цифрою 1.
a b c d e f #32 #32 5 #32 #32 2 4 #32 #32 #32 7 . 5 #26
1 2 3 4 5 6
Першим елементом списку введення є текстова змінна a максимальної довжини 5. Тому процедура зчитає перші 5 символів, встановить вказівник в позицію 2 і присвоїть змінній a значення ‘abcde’: a =‘abcde’. Другим елементом списку введення є символьна змінна b. Процедура присвоїть змінній b значення ‘f’ і переведе вказівник в позицію 3. Наступною змінною є цілочисельна змінна i. Тому процедура спочатку шукає перший символ, що не співпадає з символами #32, #10, #13, #26. В даному випадку це символ 5. Після цього шукається один із символів #32, #10, #13, #26 та встановлюється вказівник на нього. В даному прикладі в позицію 4. Якщо символи між попередньою та поточною позиціями можна трактувати як ціле число, то процедура переведе ці символи в прямий або доповняльний коди і присвоїть це значення відповідній змінній. В даному випадку #32 #32 5 можна трактувати як число, і тому змінна i набеде значення 5. Аналогічно відбувається зчитування значень змінних j=24, p=7.5.
б) файл proba1.in.
a b c d e#13 #10 f #32 #32 5 #32 #32 2 4 #32 #32 #32 7 . 5 #26.
На екрані файл зображається
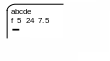
Позиції вказівника при зчитуванні з файла такі:
a b c d e #13 #10 f #32 #32 5 #32 #32 2 4 #32 #32 7 . 5 #26.
1 2 3 4
В результаті a=’abcde’ , b=#13. Символи #10, f не можуть трактуватися як ціле число і тому система видасть повідомлення Error 106: Invalid numeric format
Приклад 2.
var
a:string[5];
b:char;
i,j:integer;
p:real;
fin:text
begin
assign(fin,’proba2.in’);
reset(fin);
readln(fin,a);
read(fin,b,i,j);
readln(fin,p);
. . . . . . . . . . . . . . .
end.
а) файл proba2.in
a b c d e f 1 2 3 #13 #10 #32 #32 5 #32 #32 2 4 #32 7 . 5 #26
(підкресленні позиції вказівника при зчитуванні з файла).На екрані файл зображається



В результаті a=’abcde’ (процедура readln після зчитування значення останньої змінної переводить вказівник на перший символ наступного рядка), b=#32, i=5, j=24 ,p=7.5.
Для запису інформації у файл можна скористатися стандартними процедурами
write([файлова змінна,]список виведення);
writeln([файлова змінна,]список виведення);
Дія цих процедур ілюструється таким прикладом.
program demo_write;
var
i,j:integer;
a,b:real;
fout:text;
begin
i:=-23; j:=345;
a:=45.6; b:=23.456;
assign(fout, ‘demo_write.out));
rewrite(fout);
write(fout,’i=’,i);
writeln(fout,’ j=’, j, ‘ a=’,a:1:4);
write(fout,b:1:5);
close(fin);
end.
В результаті виконання програми буде створений текстовий файл demo_write.out:
i = - 2 3 #32 #32 j = 3 4 5 #32 #32 a = 4 5 . 46 0 0 0 #13 #10 2 3 . 4 5 6 0 0 #26
Для зчитування матриць та векторів з текстового файлу можна скористатися такими процедурами:
procedure read_vector(var f:text; var x:vector;n:size);
var
