4 Виконання роботи
Нехай задані матриці
і
.
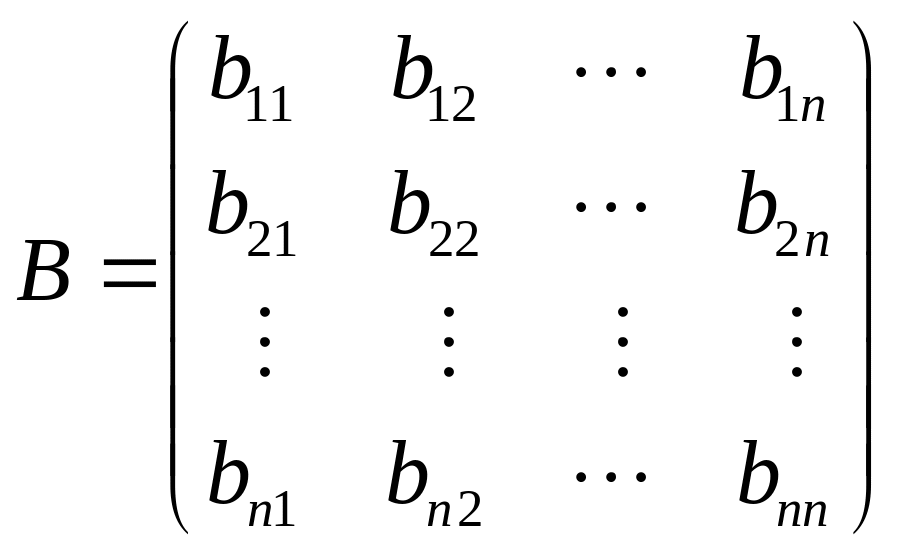Добуток цих матриць – матриця
,
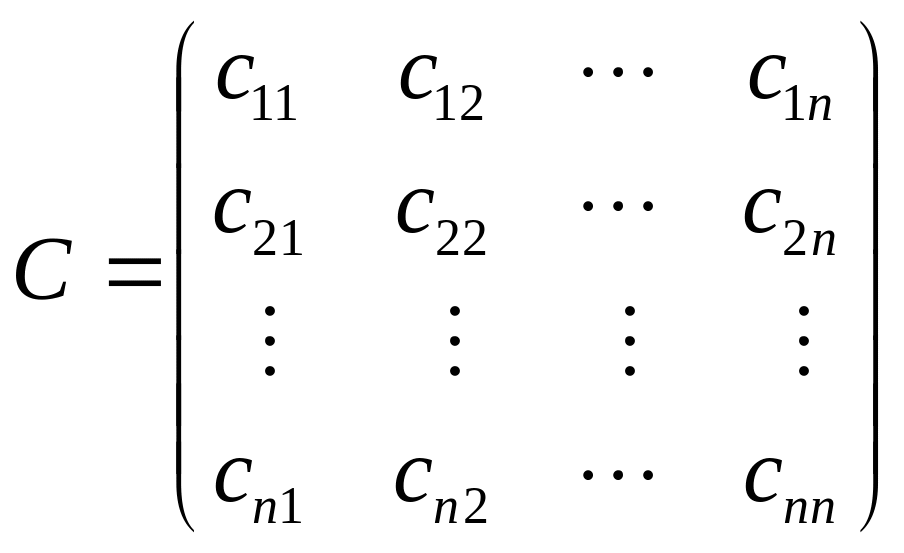елементи якої обчислюються за формулами
,
.
Програма для перемноження заданих матриць може мати вигляд.
program lab6;
const
nmax=10;
type
size=1..nmax;
matrix=array[size,size] of real;
var
a, /*Матриця
*/
b, /*Матриця
*/
c:matrix; /*Матриця
*/
i, /*поточний рядок матриці */
j, /*поточний стовпчик матриці */
n, /*порядок матриць і */
k:integer; /*індекс сумування*/
begin
/*Введення вхідних даних: n,a,b*/
repeat
write(“n=”); readln(n);
if (n>nmax) and (n<1) then
writeln(“n повинне бути додатним і не більшим ніж”,
nmax);
until (n>nmax) or (n<1);
for i:=1 to n do
for j:=1 to n do
write(“a[“,i,”,j,”]=); readln(a[I,j];
for i:=1 to n do
for j:=1 to n do
write(“b[“,i,”,j,”]=); readln(b[I,j];
/*Множення матриць*/
for i:=1 to n do
for j:=1 to n do
begin
c[i,j]=0;
for k:=1 to n do
c[i,j]= c[i,j]+a[i,k]*b[k,j];
end;
/*Виведення матриці /
for i:=1 to n do
for j:=1 to n do
if j=n then writeln(c[i,j]:1:2) else write(c[i,j]:1:2,” “)
end.
4. Варіанти завдань
1. Обчислити
координати центра ваги
системи матеріальних точок
з масами
за формулами:
.
Вхідні дані:
,
i 
1 -2.0 5.0 7.0 1.0
2 1.0 -3.0 6.0 2.0
3 -3.0 1.0 -4.0 2.0
4 4.0 4.0 -2.0 2.0
5 6.0 -1.0 1.0 1.0
2. Розв'язати лінійне рівняння
,
,
,
.
Якщо
,
то вивести на екран повідомлення “кореня
немає”,
якщо ж
,то
вивести на екран значення кореня.
Вхідні дані:
,
i
j
1 20.3 1 13.2
2 0.05 2 1.64
3 0.0 3 20.64
4 13.0 4 14.3
5 9.5
3. Обчислити
скалярний добуток векторів
та
(
)
за формулою:
Вхідні дані:
,
i 1 2 3 4 5 6
1.1 2.1 3.2 4.3 -4.1 2.1
8.2 14.3 -4.1 -2.0 -4.1 2.0
4. Обчислити
,
де
– заданий
вектор (
).
Вхідні дані: ,
.
5. Заданий вектор ( ). Знайти різницю між максимальним та мінімальним елементами вектора x.
Вхідні дані: ,
.
6. Задана квадратна
матриця
А
розміром
(
).
Необхідно знайти евклідову норму матриці
А
за формулою:
Вхідні дані: ,
.
7. Задана квадратна матриця А розміром ( ). Необхідно знайти m-норму матриці А за формулою
Вхідні дані: ,
.
8. Задана квадратна матриця А розміром ( ). Необхідно знайти l-норму матриці А по формулі:
Вхідні дані: ,
.
9. Обчислити величину
де
– елементи
матриці А
розміром
(
),
-
елементи
вектора
,
– елементи
вектора
.
В
11
,
,
,
,
.
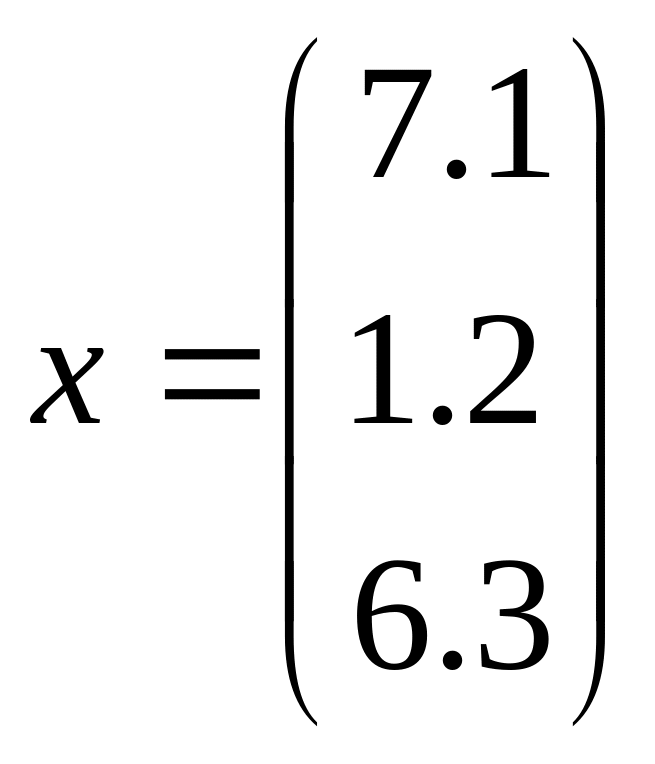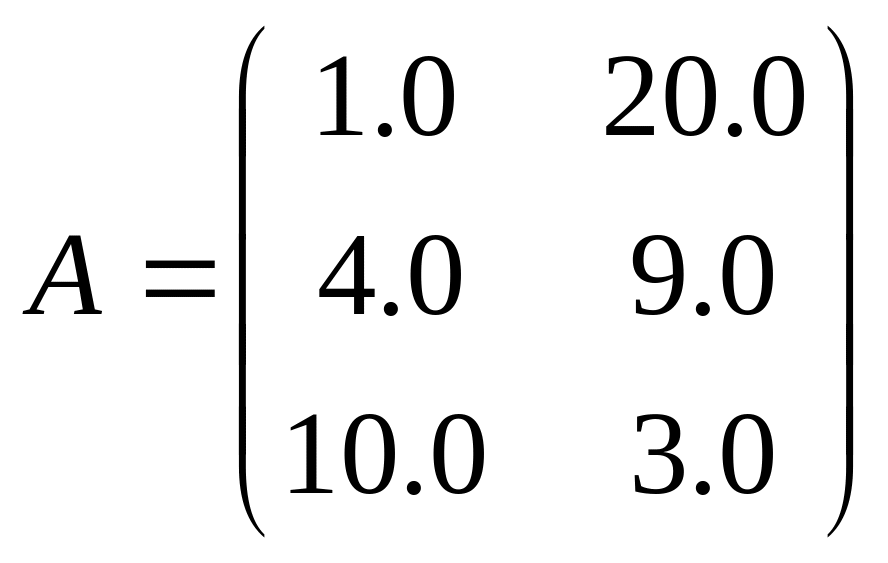10. Задані точки в
просторі
,
(
).
Обчислити довжини радіус-векторів і кути радіус-векторів з осями координат. Обчислення довжин і кутів проводити за формулами:
Вхідні дані: ,
i 1 2 3 4 5
3.9 -4.3 4.2 3.1 4.1
4.1 4.4 4.1 4.3 4.3
3.7 5.4 5.1 2.7 4.4
11. Задані точки
,
(
).
Обчислити
координати цих точок в новій системі
координат, яка повернута відносно старої
на заданий кут
(кут задається в градусах). Нові координати
точок обчислювати за
формулами
Вхідні дані:
,
,
i 1 2 3 4 5 6
2.1 3.7 -6.2 4.1 2.1 6.3
4.1 5.1 -1.5 3.1 4.1 4.1
12. Задані точки , ( ). Знайти віддаль цих точок від середньої точки з координатами
Віддаль точки
від середньої точки
обчислюється
за формулою:
Вхідні дані:
,
i 1 2 3 4 5
4.1 4.8 5.1 -4.3 4.1
-2.1 -4.1 3.1 4.3 -4.2
13. Знайти середньоквадратичне відхилення
деякої експериментальної
кривої від заданої функції
в заданих точках
,
(
).
Вхідні дані: ,
i 1 2 3 4 5
1.0 2.0 3.0 4.0 5.0
8.3 12.7 18.8 25.4 33.0,
14. Задані точки
,
(
).
Для кожної пари точок
і
(
).
Знайти коефіцієнти
,
прямої
,
яка проходить через ці дві точки.
Коефіцієнти
,
обчислюються
за формулами:
Вхідні дані: ,
i 1 2 3 4 5 6
0.5 0.9 1.4 1.5 4.1 5.1
4.1 2.1 0.8 3.1 4.2 8.3
15. Знайти максимальні
елементи матриці А
розміром
(
)
та його
індекси.
Вхідні дані: ,
.
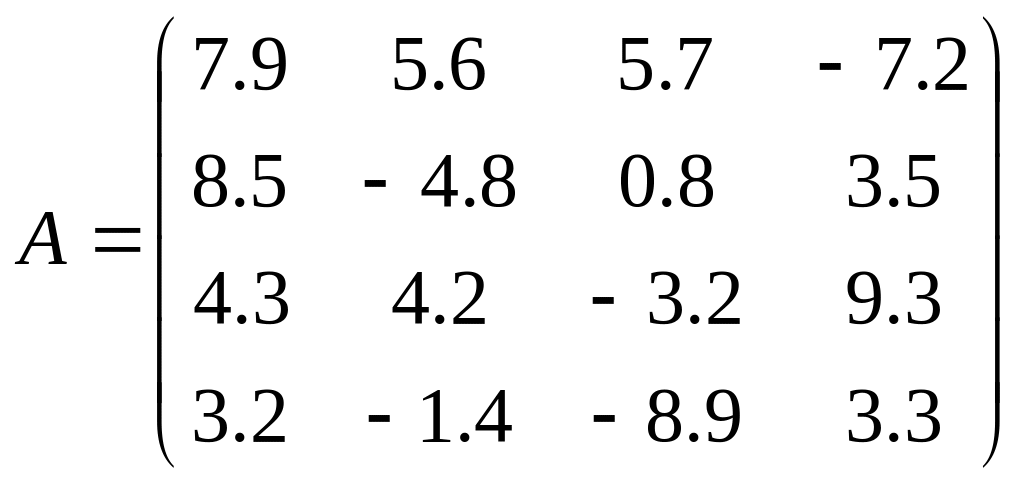16. Знайти мінімальні елементи матриці А розміром ( ) та його індекси.
В
13
.
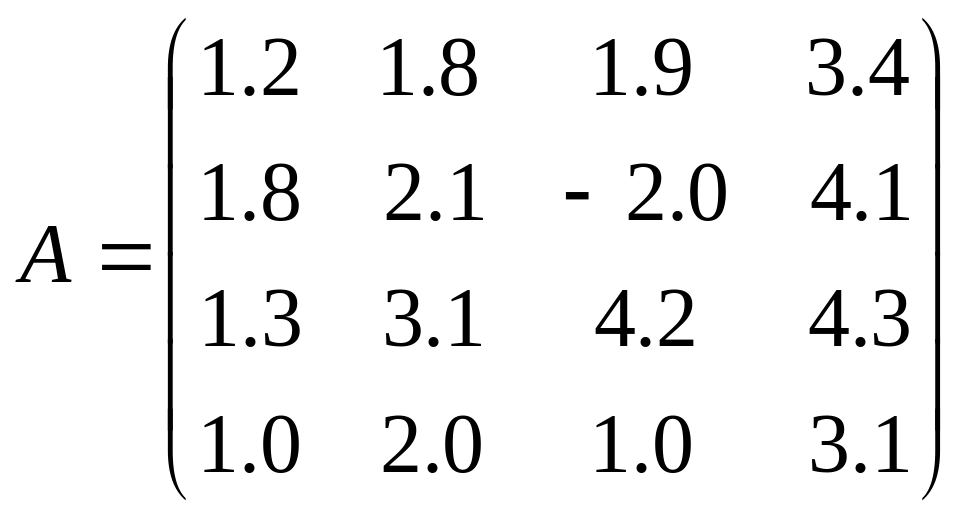17. Задана квадратна матриця А розміром ( ). Необхідно поміняти місцями k і l-рядки матриці.
Вхідні дані:
,
,
,
.
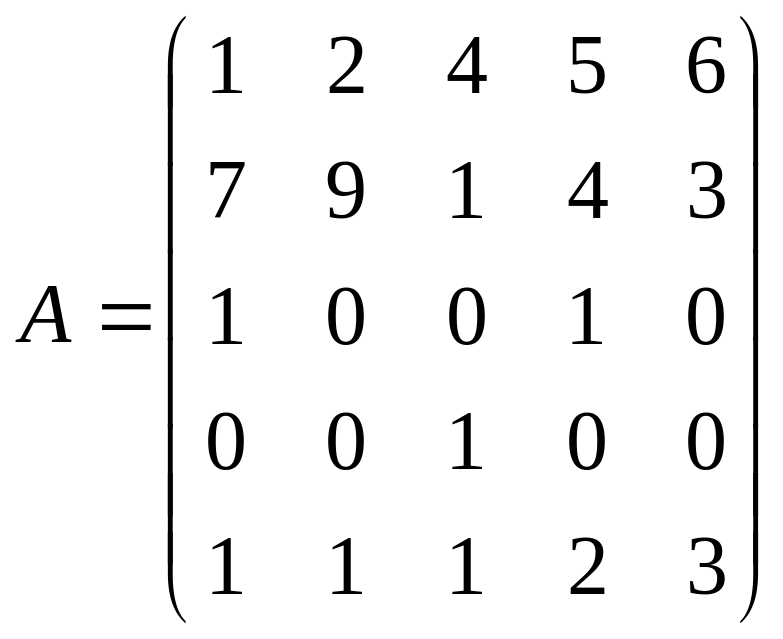18. Задана матриця А розміром і вектор . Необхідно обчислити добуток матриці А на вектор x.
Вхідні дані: ,
,
.
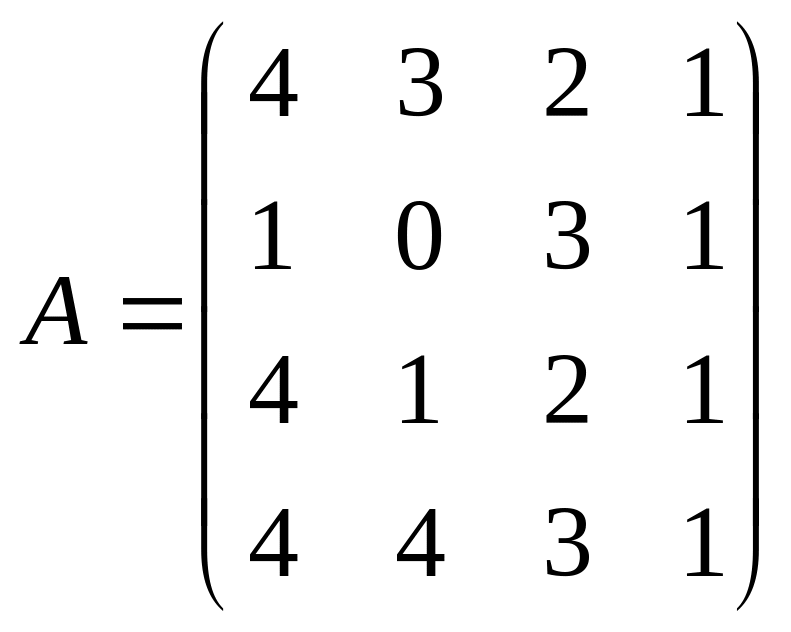19. Задані дві
матриці: А
розміром
,
B
розміром
(
).
Знайти добуток цих матриць.
Вхідні дані:
,
,
,
,
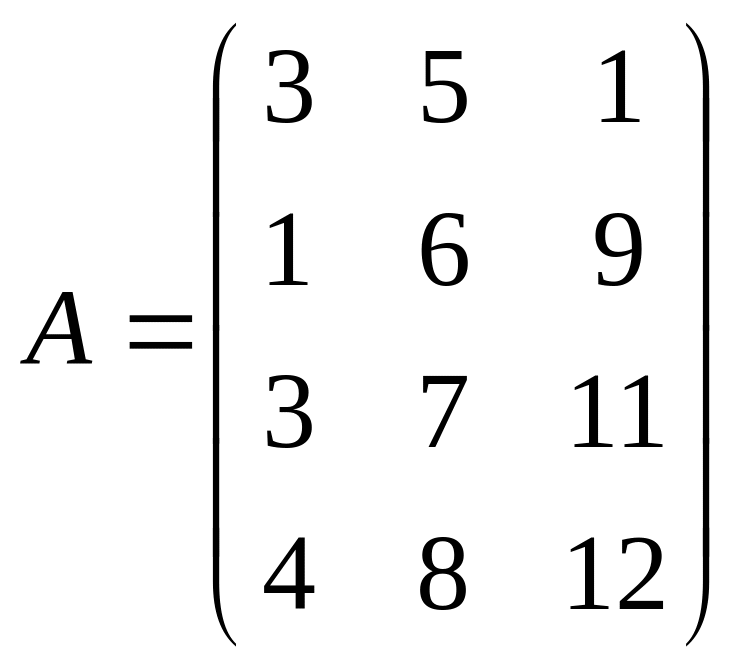20. Заданий вектор.
Перетворити його таким чином, щоб всі
його елементи належали відрізку
.
Вхідні дані:
,
i 1 2 3 4 5 6 7
1.8 1.9 2.4 -4.5 7.1 -7.1 4.3
21. Заданий вектор
(
,
– цілі
числа). Необхідно знайти кількості
додатних, від'ємних і нульових компонент
вектора.
Вхідні дані:
,
22. Обчислити
математичне сподівання вибірки
(
)
і середній модуль відхилень за формулами
,
Вхідні дані: ,
.
23. Задані два вектори та ( ). Знайти кут між ними.
Вхідні дані: n=7,
i 1 2 3 4 5 6 7
0.8 4.1 2.8 1.8 3.1 4.1 8.4
0.3 5.2 4.3 9.2 4.3 3.1 3.5
Кут між x і y обчислюється за формулами:
,
24. Задана матриця А розміром ( ). Обчислити значення величини
Вхідні дані: ,
25. Обчислити значення білінійної форми
де m – максимальний елемент вектора , – елементи матриці А розміром , – елементи вектора ( ).
В
15
,
,
