
- •11. Выходит из закона сохранения энергии. Включает в себя внутреннюю энергию и кинетическую энергию в макродвижениях
- •13.Теорема Гельмгольца.
- •15. Модель вязкой ньютоновской жидкости (газа) (определение, свойства, происхождение, физический смысл коэффициентов в выражении тензора напряжений через тензор скоростей деформаций).
- •17. Модель идеальной жидкости (газа) (определение, выражения для компонент тензора напряжений, уравнения количества движения и энергии).
- •19. Термодинамическая модель среды. Калорическое и термическое уравнения состояния. Совершенный газ. Несжимаемая жидкость.
- •23. Интеграл адиабаты (определение адиабатического течения, допущения и вывод уравнения адиабаты в общем случае, свойство баротропности).
1билет. МЖГ- это раздел механики, в котором изучаются законы движения и равновесия жидкости и газа, а так же законы их взаимод. с обтекаемыми пов-ми. Радиус ядра атома = 10-15. Боровский радиус = 5,29*10-11. Масса нейтрона 1,67*10-27. Масса электрона 9,1*10-31. В одном квадратном метре кол-во молекул в воздухе над поверхностью моря при 00 = 2,6*1019. На высоте 60 км = 8*1015. Скорость молекул кислорода = 425 мс. Скорость Н2 =1700 мс. Средняя длина пробега 6,5*10-8. Постулаты МЖГ. 1 Евклидовость пространства – это допущение означает, что реальное физическое пространство можно заменить реальным материальным пространством, в котором положение каждой точки определяется с помощью декартовой ск . 2 абсолютность времени – время течет одинаково для всех наблюдателей, вне зависимости от того, движутся они или нет. объем содержит огромное кол-во молекул, так что его средние характеристики устойчивы к изменению объема.
2
билет. индивидуальная и локальная
производные от газодинамических
параметров по времени. Скорость объемного
расширения жидкости (определение,
вычисление).
Индивидуальная
производная.
Пусть
А – некоторая газодинамическая величина.
Для выделенной жидкой частицы эта
величина будет зависеть только от
времени A=A(t).
Изменение А в предположении что эта
величина относится к фиксированной
частице, характеризуется производной
от А по времени, которая называется
индивидуальной производной.
Производная
по Эйлеру.
Пусть А – функция переменных
Эйлера. Для фиксированной частицы
координаты в соответствии с законом
ее движения будут функциями от
времени.
x=x(t),
y=y(t),
z=z(t).
=> A(t)=A[x(t),
y(t),
x(t),
t]
 Так
же:
Так
же:
 ,
,
 ,
,
 =>
=>
 Производная
по Лагранжу.
Пусть А – функция
переменных Лагранжа: А=А(a,,b,c,t).
Для выделенной частицы аргументы a,b
и c
фиксированы, меняется только время.
Поэтому:
Производная
по Лагранжу.
Пусть А – функция
переменных Лагранжа: А=А(a,,b,c,t).
Для выделенной частицы аргументы a,b
и c
фиксированы, меняется только время.
Поэтому:

Местная
производная.
Пусть
в пространстве зафиксирована некоторая
точка. Через эту точку в разные моменты
времени будут проходить частицы. Каждой
из них соответствует какая то
газодинамическая величина А. В
фиксированной точке пространства
A=A(t).
Изменение
величины А характеризуется производной
А по времени, которая называется
местной(локальной) производной.
Производная
по Эйлеру.
Пусть А – функция переменных
Эйлера, А(x,y,z,t).
Т.к. x,y,z
фиксированы то местная производная
это частная производная
 Производная
по Лагранжу.
Пусть А – функция
переменных Лагранжа: А(a,b,c,t).
В разные моменты времени через
фиксированную точку М проходят разные
частицы с разными значениями a,b,c.
Но так как в каждый момент времени в
точке М оказывается только одна частица,
то: a=a(t),
b=b(t),
c=c(t).
Для
фиксированной точки пространства
A=A(a(t),
b(t),
c(t),
t)
Производная
по Лагранжу.
Пусть А – функция
переменных Лагранжа: А(a,b,c,t).
В разные моменты времени через
фиксированную точку М проходят разные
частицы с разными значениями a,b,c.
Но так как в каждый момент времени в
точке М оказывается только одна частица,
то: a=a(t),
b=b(t),
c=c(t).
Для
фиксированной точки пространства
A=A(a(t),
b(t),
c(t),
t)
 Эта
формула приобретает значение если
известны производные значений
a,b,c.
Вычислим
их. Так как движение задано в переменных
Лагранжа, то известна связь x=x(a,b,c,t),
y=y(a,b,c,t),
z=z(a,b,c,t).
Дифференцируя по времени обе части
получим:
Эта
формула приобретает значение если
известны производные значений
a,b,c.
Вычислим
их. Так как движение задано в переменных
Лагранжа, то известна связь x=x(a,b,c,t),
y=y(a,b,c,t),
z=z(a,b,c,t).
Дифференцируя по времени обе части
получим:


 Получилась
система трех линейных уравнений
относительно производных a,b,c.
Якобиан системы не равен нулю. Решив
системы и подставляя значения в
Получилась
система трех линейных уравнений
относительно производных a,b,c.
Якобиан системы не равен нулю. Решив
системы и подставляя значения в
 , получим
, получим

Скорость
объемного расширения жидкости.
Рассмотрим в момент времени t
некоторую массу жидкости в объеме
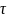 ,
ограниченном поверхностью S.
В момент t+
,
ограниченном поверхностью S.
В момент t+ та же масса жидкости будет занимать
объем
та же масса жидкости будет занимать
объем
 ,
ограниченный поверхностью
,
ограниченный поверхностью
 .
Скоростью объемного расширения жидкости
в данной точке называется предел
.
Скоростью объемного расширения жидкости
в данной точке называется предел
 .
Величина
.
Величина
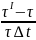 есть
относительное приращение объема в
единицу времени.
есть
относительное приращение объема в
единицу времени.
 Так
как
мало, то объем
Так
как
мало, то объем
 представляет собой тонкий слой между
поверхностями S
и SI.
Тогда элемент объема
представляет собой тонкий слой между
поверхностями S
и SI.
Тогда элемент объема
 можно взять в виде
можно взять в виде
 ,
где
,
где
 – расстояние по нормали между поверхностью
S
и поверхностью SI,
в которую перешли точки с поверхности
S
за время
.
– расстояние по нормали между поверхностью
S
и поверхностью SI,
в которую перешли точки с поверхности
S
за время
.
 - проекция скорости точек поверхности
S
на внешнюю нормаль к ней.
- проекция скорости точек поверхности
S
на внешнюю нормаль к ней.
 Представим
через проекции скорости на оси координат:
Представим
через проекции скорости на оси координат:
 .Теперь перейдем по формуле Гаусса –
Остроградского к интегралу по объему
.Теперь перейдем по формуле Гаусса –
Остроградского к интегралу по объему
 Прменим
к интегралу теорему о среднем и получим
что:
Прменим
к интегралу теорему о среднем и получим
что:
 Подставим:
Подставим:
 Когда
объем стягивается к точке, то среднее
значение дивергента будет стремиться
к этой к значению в этой точке. Таким
образом
Когда
объем стягивается к точке, то среднее
значение дивергента будет стремиться
к этой к значению в этой точке. Таким
образом

Билет 3 Понятие жидкого объема. Вывод формул для вычисления производной по времени от интеграла по жидкому объему.
Выделим
некоторую массу жидкости, и пусть она
в некоторый момент времени t
занимает объем
,
ограниченный поверхностью S.
Пусть в каждой точке (частице) этого
объёма определена некоторая
гидродинамическая величина A
( скалярная, векторная или тензорная –
безразлично). Рассмотрим интеграл.

При
перемещении выделенной массы жидкости
будут изменяться положение её частиц,
общий объём
и значение величины A
в различных точках. Интеграл есть
функция времени
 .
.

Получим
выражение для производной
 в переменных Эйлера и переменных
Лагранжа.
в переменных Эйлера и переменных
Лагранжа.
1.Вычисление
в переменных Эйлера. Рассмотрим два
близких момента времени t
и t’=t+ .
Для момента времени t
сохраним введённые обозначения:
A(x,y,z,t)=A
.
Для момента времени t
сохраним введённые обозначения:
A(x,y,z,t)=A
 .
Значение всех функций в момент t’=t+
.
Будем отмечать штрихами. Таким образом,
.
Значение всех функций в момент t’=t+
.
Будем отмечать штрихами. Таким образом,

При малых можем записать
 - >
- >

Подынтегральная
функция A’-A
вычесляется в точках, принадлежащих
объему
,
но А вычисляется в момент t,
а A’
– в момент t’=
.
С точночтью до малых более высокого
порядка

Учитывая
это, приходим к равенству

Преобразуем второе слагаемое.
Элемент
 объёма
объёма
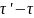 выберем в виде
выберем в виде
 Тогда
Тогда
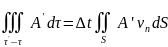
Равенство
(15.4) можно тепрь записать в виде

Разделим
обе части на
и устремим
к нулю. При этом A’
перейдёт в A,
и мы получим

Как
обычно, преобразуем интеграл по
поверхности к интегралу по объёму:

Таким образом, для производной получим выражение

Подынтегральное выражение можно преобразовать к другому виду, раскрывая производные от произведений:

Div –дивергенция (дивергенция — это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность достаточно малой (в условиях конкретной задачи) окрестности каждой внутренней точки области определения поля.)
Соответственно
равенство (15.6) примет вид

2.Вычисление в переменных Лагранжа.
Рассмотрим объём выделенной массы жидкости в момент времени t. Координаты частиц этого объёма можно записать в виде: x=x(a,b,c,t); y=y(a,b,c,t); z=z(a,b,c,t)
Где
a,b,c
– координаты этих частиц в момент
времени
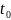 ,
когда декартовы координаты совпадали
с координатами Лагранжа x=a,
y=b,
z=c,
а объём
занимал объём
,
когда декартовы координаты совпадали
с координатами Лагранжа x=a,
y=b,
z=c,
а объём
занимал объём
 .
В интеграле (15.1), который нужно
дифференцировать, перейдём от переменных
x,y,z
к переменным Лагранжа. Тогда
.
В интеграле (15.1), который нужно
дифференцировать, перейдём от переменных
x,y,z
к переменным Лагранжа. Тогда

Но
в этом случае объём интегрирования
постоянен для всех моментов времени,
и можно дифференцировать под знаком
интеграла. Таким образом

Сделаем
переход в правой части равенства от
переменных a,
b,
c
к переменным x,
y,
z,
учитывая при этом, что

Тогда
получим

Билет
4. Закон
сохранения массы (допущения, физическая
формулировка, вывод уравнения закона
в интегральной форме. Уравнение
неразрывности (вывод, рассмотрение
частных случаев).
Закон
сохранения масс
– это физический закон, справедливый
для движений, происходящих со скоростями,
незначительными по сравнению со
скоростью света.
Предположим
что в процессе движения жидкости нет
ни возникновения ни, ни исчезновение
массы.
 .
По определению плотности
.
По определению плотности
 масса в объеме
равна
масса в объеме
равна
 .
Масса в объемах
и
ровна:
.
Масса в объемах
и
ровна:
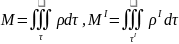 тогда
тогда
 или
или
 .
Теперь пусть в объем
в
течении времени
.
Теперь пусть в объем
в
течении времени
 поступает масса жидкости
поступает масса жидкости
 ,
q
– плотность источников. Масса жидкости,
которая в момент времени находилась в
объеме будет изменяться во время
движения. За время dt
она получит приращение
,
q
– плотность источников. Масса жидкости,
которая в момент времени находилась в
объеме будет изменяться во время
движения. За время dt
она получит приращение
 .
За промежуток времени от t
до tI
приращение
массы будет равно
.
За промежуток времени от t
до tI
приращение
массы будет равно
 .
Теперь можем записать 𝑀I=𝑀+∆𝑀.
Подставляем:
.
Теперь можем записать 𝑀I=𝑀+∆𝑀.
Подставляем:
 .
Это равенство – запись закона
сохранения масс при наличии
пространственно-распределенных
источников
для конечного
объема и конечного промежутка времени.
Теперь запишем для для бесконечно
малого промежутка времени.
.
Это равенство – запись закона
сохранения масс при наличии
пространственно-распределенных
источников
для конечного
объема и конечного промежутка времени.
Теперь запишем для для бесконечно
малого промежутка времени.
 .
.
 Поделив
на
и
устремив
к
нулю, получим
Поделив
на
и
устремив
к
нулю, получим
 .
Это
равенство – запись закона сохранения
масс для конечного объема для данного
момента времени при наличии
пространственно-распределенных
источников.
.
Это
равенство – запись закона сохранения
масс для конечного объема для данного
момента времени при наличии
пространственно-распределенных
источников.
Уравнение
неразрывности.
 .
Подставив
в уравнение выше мы получим:
.
Подставив
в уравнение выше мы получим:
 Это
равенство имеет место для любого объема
тао. Это возможно только когда
подынтегральная функция равна нулю.
Следовательно:
Это
равенство имеет место для любого объема
тао. Это возможно только когда
подынтегральная функция равна нулю.
Следовательно:
 Раскрывая
в этой формуле производные от произведений
и вводя обозначение индивидуальной
производной
Раскрывая
в этой формуле производные от произведений
и вводя обозначение индивидуальной
производной
 получим:
получим:
 Получившаяся
формула и есть запись закона сохранения
масс в дифференциальной форме.
Пусть
жидкость не сжимаема. Это означает, что
плотность в движущейся частице не
изменяется, то есть индивидуальная
производная от плотности по времени
равна нулю.
Получившаяся
формула и есть запись закона сохранения
масс в дифференциальной форме.
Пусть
жидкость не сжимаема. Это означает, что
плотность в движущейся частице не
изменяется, то есть индивидуальная
производная от плотности по времени
равна нулю.
 Уравнение
неразрывности в этом случае имеет вид
Уравнение
неразрывности в этом случае имеет вид
 .
Рассмотрим
уравнение, когда q=0.
.
Рассмотрим
уравнение, когда q=0.
 Вводя
вектор
Вводя
вектор
 с проекциями
с проекциями
 ,
можно уравнение переписать:
,
можно уравнение переписать:

 Частные
случаи:
1 Движение установившееся.
В этом случае местная производная
Частные
случаи:
1 Движение установившееся.
В этом случае местная производная
 равна нулю:
равна нулю:
 2
Жидкость не сжимаема. В этом случае
.
Следовательно:
2
Жидкость не сжимаема. В этом случае
.
Следовательно:
 3
Движение плоское. Движение называется
плоским, если существует такая плоскость,
что все частицы жидкости движутся
параллельно этой плоскости, причем на
любой прямой, перпендикулярной этой
плоскости, гидродинамические величины
имею одно и то же значение. Принимая
эту плоскость за плоскость (x,y)
получим что
3
Движение плоское. Движение называется
плоским, если существует такая плоскость,
что все частицы жидкости движутся
параллельно этой плоскости, причем на
любой прямой, перпендикулярной этой
плоскости, гидродинамические величины
имею одно и то же значение. Принимая
эту плоскость за плоскость (x,y)
получим что
 =0.
Следовательно:
=0.
Следовательно:
 .
Если
движение установившееся то:
.
Если
движение установившееся то:
 Если
несжимаемая жидкость то:
Если
несжимаемая жидкость то:
 4
Одномерное движение с плоской
симметрией.
Частица движется по
прямой х.
4
Одномерное движение с плоской
симметрией.
Частица движется по
прямой х.
 Уравнение
неразрывности в этом
Уравнение
неразрывности в этом
Билет
5. Объемные
и поверхностные силы в сплошной среде
(определение плотности объемных и
массовых сил и ее вычисление в случае
действия сил тяжести, определение
напряжений, вычисление главных векторов
объемных и поверхностных сил). Закон
изменения количества движения для
движущегося жидкого объема (физическая
формулировка, интегральная форма
записи).
Объемные
(далее массовые) силы – силы, действующие
на каждый элемент объема независимо
от того, имеются ли рядом другие части
жидкости. Пусть FM
– главный вектор сил, действующих на
массу М жидкости, заполняющей объем τ.
Средней массовой силой, действующей
на массу М, называют величину
 Вектор
Вектор
 называется массовой силой, действующей
в этой точке.
На объем
с массой
действует сила
называется массовой силой, действующей
в этой точке.
На объем
с массой
действует сила
 .
Отсюда главный вектор массовых сил
будет:
.
Отсюда главный вектор массовых сил
будет:
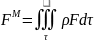 Поверхностные
силы. Пусть объем τ
ограничен поверхностью S.
Жидкость, находящаяся вне объема,
действует через поверхность S
на жидкость внутри объема. Силы, с
которыми частицы жидкости, находящиеся
снаружи поверхности S,
действуют на поверхностные частицы
объема, называют поверхностными.
Выделим
на S
элемент поверхности
Поверхностные
силы. Пусть объем τ
ограничен поверхностью S.
Жидкость, находящаяся вне объема,
действует через поверхность S
на жидкость внутри объема. Силы, с
которыми частицы жидкости, находящиеся
снаружи поверхности S,
действуют на поверхностные частицы
объема, называют поверхностными.
Выделим
на S
элемент поверхности
 с нормалью n. Главный вектор поверхностных
сил, действующий на
,
обозначим
с нормалью n. Главный вектор поверхностных
сил, действующий на
,
обозначим
 .
Среднее напряжение, действующее на
площадку
,
будет
.
Среднее напряжение, действующее на
площадку
,
будет
 .
Пусть площадка
стягивается в точку.
Вектор:
.
Пусть площадка
стягивается в точку.
Вектор:
 называют напряжением поверхностных
сил, действующим в рассматриваемой
точке.
Главный вектор поверхностных
сил, действующих на поверхность S:
называют напряжением поверхностных
сил, действующим в рассматриваемой
точке.
Главный вектор поверхностных
сил, действующих на поверхность S:
 Поверхностные
силы описывают взаимодействие между
различными областями жидкости.
Интегральная
запись закона количества движения.
Выделим
в движущейся жидкости некоторый объем
τ,
ограниченный поверхностью S.
Пусть вектор К – количество движения
массы жидкости, заполняющей этот объем.
В элементарном объеме
заключена масса
Поверхностные
силы описывают взаимодействие между
различными областями жидкости.
Интегральная
запись закона количества движения.
Выделим
в движущейся жидкости некоторый объем
τ,
ограниченный поверхностью S.
Пусть вектор К – количество движения
массы жидкости, заполняющей этот объем.
В элементарном объеме
заключена масса
 .
Количество движения этой масс, имеющей
скорость v:
.
Количество движения этой масс, имеющей
скорость v:
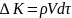 .
Количество
движения массы, заключенной в объеме
τ:
.
Количество
движения массы, заключенной в объеме
τ:
 Для
выделенной массы жидкости вектор К,
как и объем – это функции времени.
Закон
количества движения можно сформулировать
так: производная по времени от количества
движения некоторой системы масс равна
главному вектору внешних сил, действующих
на эту систему, следовательно:
Для
выделенной массы жидкости вектор К,
как и объем – это функции времени.
Закон
количества движения можно сформулировать
так: производная по времени от количества
движения некоторой системы масс равна
главному вектору внешних сил, действующих
на эту систему, следовательно:

 Проинтегрировав
от t1
до t2
, получим
запись закона для конечного промежутка
времени:
Проинтегрировав
от t1
до t2
, получим
запись закона для конечного промежутка
времени:
 .
(2)
Изменение количества движения за
некоторый промежуток времени равно
сумме импульса массовых сил и импульса
поверхностных сил.
.
(2)
Изменение количества движения за
некоторый промежуток времени равно
сумме импульса массовых сил и импульса
поверхностных сил.

 Равенства
1,2 и 3 дают интегральную запись закона
количества движения.
Равенства
1,2 и 3 дают интегральную запись закона
количества движения.
Билет
6 Формула
Коши (вывод). Тензор напряжений (запись
формулы Коши в терминах понятий линейной
алгебры, введение линейного оператора
 и его физический смысл, определение
тензора напряжений).
Запишем
закон количества движения для частного
случая объема. За объем выберем тетраэдр,
три грани которого параллельны
координатным плоскостям. Обозначим
площади этих граней через Sx
, Sy
, Sz
. Внешние
нормали к этим граням направлены
противоположно осям Ox,
Oy,
Oz.
Площадь четвертой грани с нормалью n
обозначим Sn.
Пусть
и его физический смысл, определение
тензора напряжений).
Запишем
закон количества движения для частного
случая объема. За объем выберем тетраэдр,
три грани которого параллельны
координатным плоскостям. Обозначим
площади этих граней через Sx
, Sy
, Sz
. Внешние
нормали к этим граням направлены
противоположно осям Ox,
Oy,
Oz.
Площадь четвертой грани с нормалью n
обозначим Sn.
Пусть
 - напряжения , действующие на каждую из
граней.
- напряжения , действующие на каждую из
граней.
 Площади
Площади
 - проекции
- проекции
 на оси x,
y,
z:
на оси x,
y,
z:
 h
– высота тетраэдра.
h
– высота тетраэдра.
 Применив
теорему о среднем, получим:
Применив
теорему о среднем, получим:
 Раздели
обе части уравнения на Sn
и устремим к нулю h.
а
Раздели
обе части уравнения на Sn
и устремим к нулю h.
а
 Рассмотрим
площадку ∆S
с внешней нормалью l.
Сила с которой жидкость, находящаяся
по ту сторону площадки, куда направлена
нормаль l,
действует на жидкость, находящуюся по
другую сторону площадки, равна
Рассмотрим
площадку ∆S
с внешней нормалью l.
Сила с которой жидкость, находящаяся
по ту сторону площадки, куда направлена
нормаль l,
действует на жидкость, находящуюся по
другую сторону площадки, равна
 .
На ряду с l
введем нормаль –l.
Соответственно определению получим
силу
.
На ряду с l
введем нормаль –l.
Соответственно определению получим
силу
 .
По закона равенства действия и
противодействия
.
По закона равенства действия и
противодействия
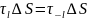 .
Следовательно:
.
Следовательно:



 Формула
коши, дает
возможность вычислить напряжение в
точке на площадке с нормалью n,
если известны напряжения, действующие
на площадки, перпендикулярные
соответствующим осям координат.
Из
формулы Коши следует, что инапряжение
в точке как угодно ориентированной
площадки может быть вычислено, если
известна таблица из 9-ти величин:
Формула
коши, дает
возможность вычислить напряжение в
точке на площадке с нормалью n,
если известны напряжения, действующие
на площадки, перпендикулярные
соответствующим осям координат.
Из
формулы Коши следует, что инапряжение
в точке как угодно ориентированной
площадки может быть вычислено, если
известна таблица из 9-ти величин:
 Тензор
напряжений.
Будем
исходить из формулы Коши. Докажем, что
таблица выше, является аффинным
ортогональным тензором второго ранга.
Для этого надо найти формулы преобразования
Тензор
напряжений.
Будем
исходить из формулы Коши. Докажем, что
таблица выше, является аффинным
ортогональным тензором второго ранга.
Для этого надо найти формулы преобразования
 при переходе от одной системы координат
x,
y,
z
к другой x’,
y’,
x’
.
Обозначим орты координатных осей
соответственно через i,
j,
k.
По таблице для направляющих косинусов
при переходе от одной системы координат
x,
y,
z
к другой x’,
y’,
x’
.
Обозначим орты координатных осей
соответственно через i,
j,
k.
По таблице для направляющих косинусов
 и формуле коши, выбирая за n
последовательно i’,
j’,
k’.
Получим:
и формуле коши, выбирая за n
последовательно i’,
j’,
k’.
Получим:


 Рассмотрим
одну из этих формул. Представим
Рассмотрим
одну из этих формул. Представим
 через проекции
через проекции

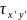
 на оси x’,
y’,
z’:
на оси x’,
y’,
z’:
 Аналогично
через проекции x,
y,
z.
Подставив
получим векторное равенство:
Аналогично
через проекции x,
y,
z.
Подставив
получим векторное равенство:
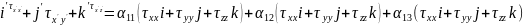 Умножая
последовательно скалярно на i’,
j’,
k’,
получим выражения для
через составляющие таблицы T
в координатах (x,y,z).
Выпишем одно из равенств:
Умножая
последовательно скалярно на i’,
j’,
k’,
получим выражения для
через составляющие таблицы T
в координатах (x,y,z).
Выпишем одно из равенств:
 Из
этого выражения видно, что составляющие
таблицы Т при переходе от одной системы
координат к другой преобразуются как
компоненты аффинного ортогонального
тензора второго ранга. Тензор
Из
этого выражения видно, что составляющие
таблицы Т при переходе от одной системы
координат к другой преобразуются как
компоненты аффинного ортогонального
тензора второго ранга. Тензор
 называется тензором напряжений.
Физический
смысл.
Возьмем вектор
называется тензором напряжений.
Физический
смысл.
Возьмем вектор
 - напряжение на площадку, перпендикулярную
оси х:
- напряжение на площадку, перпендикулярную
оси х:
 Здесь
Здесь
 - нормальное напряжение;
- нормальное напряжение;
 ,
,
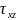 ,
являющиеся проекциями вектора
на оси координат y,
z,
есть напряжения, касательные
площадке.
Таким образом, диагональные
компоненты тензора дают нормальные
составляющие напряжений, боковые
компоненты дают касательные составляющие
напряжений, приложенных к площадкам,
перпендикулярным осям координат.
,
являющиеся проекциями вектора
на оси координат y,
z,
есть напряжения, касательные
площадке.
Таким образом, диагональные
компоненты тензора дают нормальные
составляющие напряжений, боковые
компоненты дают касательные составляющие
напряжений, приложенных к площадкам,
перпендикулярным осям координат.
Билет
7. Уравнения
динамики сплошной среды в напряжениях
(вывод).
Исходим
из интегральной записи закона количества
движения:
 Используя
для
Используя
для
 формулу
Коши, преобразуем интеграл по S
в правой части к интегралу по объему
τ,
применяя формулу Гаусса-Остроградского:
формулу
Коши, преобразуем интеграл по S
в правой части к интегралу по объему
τ,
применяя формулу Гаусса-Остроградского:
 Подставляя,
получаем интегральную запись закона
в виде:
Подставляя,
получаем интегральную запись закона
в виде:
 Так
как эта формула имеет место для любого
объема тао, то, следовательно:
Так
как эта формула имеет место для любого
объема тао, то, следовательно:
 Выполнив
дифференцирование в первом слагаемом,
можем переписать:
Выполнив
дифференцирование в первом слагаемом,
можем переписать:
 Эти
два равенства представляют собой
дифференциальную запись закона
количества движения в общем
случае.
Предположим, что движение
сплошной среды происходит при отсутствии
источников массы, т.е. q=0.
В этом случае уравнение неразрывности
имеет вид
Эти
два равенства представляют собой
дифференциальную запись закона
количества движения в общем
случае.
Предположим, что движение
сплошной среды происходит при отсутствии
источников массы, т.е. q=0.
В этом случае уравнение неразрывности
имеет вид
 .
Учитывая это, получим запись закона
количества движения в векторной форме:
.
Учитывая это, получим запись закона
количества движения в векторной форме:
 Или
в проекции на оси координат:
Или
в проекции на оси координат:


 Слува
в уравнениях стоит оператор полной
производной. Эти 4 уравнения называют
уравнениями движения сплошной среды
в напряжении.
Слува
в уравнениях стоит оператор полной
производной. Эти 4 уравнения называют
уравнениями движения сплошной среды
в напряжении.
Билет
8. Орбитальный
и внутренний моменты в жидкостях и
газах (физический смысл, определение).
Вычисление главного момента внешних
сил, приложенных к жидкому объему. Закон
изменения момента количества движения
для жидкого объема (физическая
формулировка, уравнение закона в
интегральной форме).
Рассмотрим
массу сплошной среды М. Пусть в данный
момент она занимает объем тао, ограниченный
поверхностью S.
Эта масса обладает количеством движения
К и моментом количества движения L.
Элемент объема dτ
содержит
массу
,
количество движения которой равно
 .
Момент количества движения этой массы
относительно начала координат равен
.
Момент количества движения этой массы
относительно начала координат равен
 .
Этот момент связан с поступательным
движение и часто называется орбитальным
моментом. Для области тао:
.
Этот момент связан с поступательным
движение и часто называется орбитальным
моментом. Для области тао:
 У
большинства жидкостей полный момент
иногда совпадает с орбитальным, но не
всегда. Жидкость имеет молекулярное
строение, и состояние жидкости связано
с движение молекул и их взаимодействием.
Столкновения молекул между собой
приводят к их вращению. Вращение каждой
молекулы можно охарактеризовать
вектором внутреннего момента количества
движения. В обычных условиях в силу
хаотичности движения сумма внутренних
моментов количества движения равна
нулю. В тех же случаях, когда распределение
этих моментов не изотропное, суммарный
внутренний момент оказывается отличным
от нуля. В связи с этим при рассмотрении
макроскопического движения частиц,
необходимо вводить вектор внутреннего
момента. Полный момент количества
движения частицы складывается из
орбитального момента
У
большинства жидкостей полный момент
иногда совпадает с орбитальным, но не
всегда. Жидкость имеет молекулярное
строение, и состояние жидкости связано
с движение молекул и их взаимодействием.
Столкновения молекул между собой
приводят к их вращению. Вращение каждой
молекулы можно охарактеризовать
вектором внутреннего момента количества
движения. В обычных условиях в силу
хаотичности движения сумма внутренних
моментов количества движения равна
нулю. В тех же случаях, когда распределение
этих моментов не изотропное, суммарный
внутренний момент оказывается отличным
от нуля. В связи с этим при рассмотрении
макроскопического движения частиц,
необходимо вводить вектор внутреннего
момента. Полный момент количества
движения частицы складывается из
орбитального момента
 ,
связанного с движением частицы, как
целого, и внутреннего момента количества
движения, представляющего собой
суммарный момент вращений молекул.
Обозначим через М внутренний момент
кол. движ., которым обладает единица
массы жидкости M=M(r,t).
Масса
будет обладать моментом
,
связанного с движением частицы, как
целого, и внутреннего момента количества
движения, представляющего собой
суммарный момент вращений молекул.
Обозначим через М внутренний момент
кол. движ., которым обладает единица
массы жидкости M=M(r,t).
Масса
будет обладать моментом
 .
Для массы в объеме тао получим:
.
Для массы в объеме тао получим:
 Полный
момент равен
Полный
момент равен
 Изменение
полного момента кол. движ. связано с
наличием моментов, порождаемых силовыми
полями – полем массовых и поверхностных
сил., наличием объемно-распределенных
источников внутреннего момента и потока
внутреннего момента через поверхность.
Главный орбитальный момент массовых
сил
Изменение
полного момента кол. движ. связано с
наличием моментов, порождаемых силовыми
полями – полем массовых и поверхностных
сил., наличием объемно-распределенных
источников внутреннего момента и потока
внутреннего момента через поверхность.
Главный орбитальный момент массовых
сил
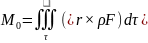 Главный
орбитальный момент поверхностных сил:
Главный
орбитальный момент поверхностных сил:
 Пусть
за время dt
в объеме dτ
порождается
момент
Пусть
за время dt
в объеме dτ
порождается
момент
 ,
где П – момент, отнесенный к единице
массы и единице времени. Обозначая
через
,
где П – момент, отнесенный к единице
массы и единице времени. Обозначая
через
 при ращение за то же время внутреннего
момента в объеме тао, получим для
при ращение за то же время внутреннего
момента в объеме тао, получим для
 выражение:
выражение:
 Через
элемент поверхности dS
с нормалью n
в течение времени dt
проникает момент
Через
элемент поверхности dS
с нормалью n
в течение времени dt
проникает момент
 .
Здесь пи – плотность потока внутреннего
момента. Обозначая через
поток за время dt
внутреннего момента через поверхность
S,
получаем:
.
Здесь пи – плотность потока внутреннего
момента. Обозначая через
поток за время dt
внутреннего момента через поверхность
S,
получаем:
 Производная
по времени от полного момента кол. движ.
L
равна сумме перечисленных 4-х моментов.
Таким образом закон момента кол. движ.
запишется в виде:
Производная
по времени от полного момента кол. движ.
L
равна сумме перечисленных 4-х моментов.
Таким образом закон момента кол. движ.
запишется в виде:
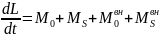
 Рассмотрим
левую часть равенства. Преобразуем
первое слагаемое:
Рассмотрим
левую часть равенства. Преобразуем
первое слагаемое:
 Выпишем
подынтегральное выражение:
Выпишем
подынтегральное выражение:
 Будем
предполагать, что в области, занятой
жидкостью, нет источников массы (q=0).
Тогда, в силу уравнения неразрывности
второе уравнение правой части обращается
в ноль:
Будем
предполагать, что в области, занятой
жидкостью, нет источников массы (q=0).
Тогда, в силу уравнения неразрывности
второе уравнение правой части обращается
в ноль:
 Интеграл
этот в таком случае можно трактовать
как момент сил инерции, взятый с обратным
знаком. Аналогичные преобразования
выражения для
Интеграл
этот в таком случае можно трактовать
как момент сил инерции, взятый с обратным
знаком. Аналогичные преобразования
выражения для
 дадут:
дадут: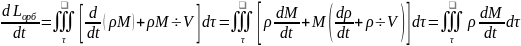 Таким
образом получаем:
Таким
образом получаем:
 Закон
момента кол. движ. можно переписать в
виде:
Закон
момента кол. движ. можно переписать в
виде:
 Преобразуем
интегралы по поверхности в интегралы
по объему. Воспользуемся формулой Коши
для
:
Преобразуем
интегралы по поверхности в интегралы
по объему. Воспользуемся формулой Коши
для
:
 Подставив
одно уравнение в другое и сгруппировав
некоторые слагаемые мы поучим:
Подставив
одно уравнение в другое и сгруппировав
некоторые слагаемые мы поучим:
 Второе
слагаемое равно нулю в силу заона
количества движения. Окончательно
закон записывается в виде:
Второе
слагаемое равно нулю в силу заона
количества движения. Окончательно
закон записывается в виде:

Билет
9. Доказательство симметрии тензора
напряжений в жидкости без внутренних
моментов.
Рассмотри
функцию
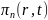 .
Применяя закон сохранения моментов к
тетраэдру и действуя так же, как и при
выводе формулы Коши, получим аналогичную
связь между
.
Применяя закон сохранения моментов к
тетраэдру и действуя так же, как и при
выводе формулы Коши, получим аналогичную
связь между
 ,
,
 ,
,
 ,
,
 :
:
 Поток
внутреннего момента будет полностью
определен, если задана таблица
составляющих псевдовекторов
,
,
Поток
внутреннего момента будет полностью
определен, если задана таблица
составляющих псевдовекторов
,
,
 Таблица
Таблица
 – аффинный ортогональный псевдотензор
второго ранга.
Преобразуем интеграл
момента количества движения к объемному,
используя (1):
– аффинный ортогональный псевдотензор
второго ранга.
Преобразуем интеграл
момента количества движения к объемному,
используя (1):
 С
учетом этой формулы закон момента
количества движения в интегральной
форме запишется в виде:
С
учетом этой формулы закон момента
количества движения в интегральной
форме запишется в виде:
 Так
как объем тао произволен, то подынтегральное
выражение должно быть равным нулю.
Отсюда:
Так
как объем тао произволен, то подынтегральное
выражение должно быть равным нулю.
Отсюда:
 это
равенство – дифференциальная запись
закона момента количества движения.
Из нее следует, что сто существуют
следующая связь между законом сохранения
момента и симметричностью тензора
напряжений.
1. Если жидкость без
внутреннего момента кол. движ., т.е. М=0,
поле таково, что внутренний момент не
возникает в объеме, т.е. П=0 и
это
равенство – дифференциальная запись
закона момента количества движения.
Из нее следует, что сто существуют
следующая связь между законом сохранения
момента и симметричностью тензора
напряжений.
1. Если жидкость без
внутреннего момента кол. движ., т.е. М=0,
поле таково, что внутренний момент не
возникает в объеме, т.е. П=0 и 
 =0,
то по формуле:
=0,
то по формуле:
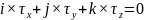 В
развернутом виде это равенство дает
В
развернутом виде это равенство дает
 Из
этого равенства следует симметрия
тензора напряжений:
Из
этого равенства следует симметрия
тензора напряжений:
 2.
Если среда такова, что тензор напряжений
у нее симметричен, то закон момента
количества движения приобретает вид:
2.
Если среда такова, что тензор напряжений
у нее симметричен, то закон момента
количества движения приобретает вид:
 Физически
это означает, что в жидкости действуют
два независимых закона: закон сохранения
орбитального момента и закон сохранения
внутреннего момента, причем закон
сохранения орбитального момента
является следствием закона сохранения
количества движения.
Физически
это означает, что в жидкости действуют
два независимых закона: закон сохранения
орбитального момента и закон сохранения
внутреннего момента, причем закон
сохранения орбитального момента
является следствием закона сохранения
количества движения.
Билет
10. Внутренняя,
кинетическая и полная энергия жидкости
и газа (физический смысл, вычисление).
Физические причины изменения полной
энергии в движущемся жидком объеме и
их математическое описание. Закон
изменения полной энергии в движущейся
жидкости (газе) (физическая формулировка,
интегральная форма записи).
Рассмотрим
сначала некоторую покоящуюся однородн.
массу жидкости М в объеме τ.
Пусть
О означает ее исходное состояние,
которое определяется некотором набором
параметров. В результате нагрева, сжатия
и других воздействий масса жидкости
перейдет в новое состояние, определяемое
другими значениями параметров. Переход
массы жидкости из исходного положения
О в другое связан с изменениями ∆ε
энергии. Будем считать, что в исходном
состоянии масса М имела запас энергии
 .
Тогда
можно ввести величину:
.
Тогда
можно ввести величину:
 .
Если
каким то образом выбрана величина
и известно ∆ε
экспериментально или теоретически то
для любого нового состояния величина
ε
может быть определена по формуле. Таким
образом, через ∆ε
определяется величина внутренней
энергии Е данной массы жидкости.
Естественно ввести величину ε
– внутреннюю энергию, отнесенную к
единице массы. В общем случае неоднородной
движущейся жидкости ε
– функция координат и времени:
.
Если
каким то образом выбрана величина
и известно ∆ε
экспериментально или теоретически то
для любого нового состояния величина
ε
может быть определена по формуле. Таким
образом, через ∆ε
определяется величина внутренней
энергии Е данной массы жидкости.
Естественно ввести величину ε
– внутреннюю энергию, отнесенную к
единице массы. В общем случае неоднородной
движущейся жидкости ε
– функция координат и времени:
 Из
этого определения следует, что запас
внутренней энергии в масс dm
равен
Из
этого определения следует, что запас
внутренней энергии в масс dm
равен
 .
Внутренняя энергия конечной массы
жидкости в объеме тао:
.
Внутренняя энергия конечной массы
жидкости в объеме тао:
 Для
совершенного газа, находящегося в
состоянии термодинамического равновесия,
уравнение состояния которого есть
уравнение Клапейрона
Для
совершенного газа, находящегося в
состоянии термодинамического равновесия,
уравнение состояния которого есть
уравнение Клапейрона
 ,
внутренняя энергия зависит только от
температуры. Выражение для внутренней
энергии имеет вид:
,
внутренняя энергия зависит только от
температуры. Выражение для внутренней
энергии имеет вид:
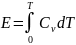 где
где
 - теплоемкость при постоянном объеме.
Здесь
в качестве исходного берется состояние,
в котором абсолютная температура равна
нулю. Когда нет процессов диссоциации
и ионизации, внутренняя энергия состоит
из энергии поступательного
- теплоемкость при постоянном объеме.
Здесь
в качестве исходного берется состояние,
в котором абсолютная температура равна
нулю. Когда нет процессов диссоциации
и ионизации, внутренняя энергия состоит
из энергии поступательного
 и вращательного
и вращательного
 и колебательного
и колебательного
 движения молекул. Для одноатомного
гада
движения молекул. Для одноатомного
гада
 .
Для случая двухатомного газа в
определенном диапазоне температур,
когда практически возбуждены только
поступательные и вращательные энергии
молекул, теплоемкость постоянна и
.
Для случая двухатомного газа в
определенном диапазоне температур,
когда практически возбуждены только
поступательные и вращательные энергии
молекул, теплоемкость постоянна и
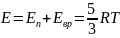 .
При боле высоких температурах начинает
сказываться возбуждение колебательной
энергии молекул. Теплоемкость
.
При боле высоких температурах начинает
сказываться возбуждение колебательной
энергии молекул. Теплоемкость
 колебательных степеней свободы зависит
от температуры, и внутренняя энергия
модет быть подставлена в виде
колебательных степеней свободы зависит
от температуры, и внутренняя энергия
модет быть подставлена в виде
 Зависимость
от T
известна.
Зависимость
от T
известна.
Полная
энергия. Если жидкость движется, то она
обладает кинетической энергией.
Кинетическая энергия
 массы dm,
движущейся со скоростью
массы dm,
движущейся со скоростью
 ,
равна
,
равна
 .
Кинетическая
энергия массы, заключенной в объем тао:
.
Кинетическая
энергия массы, заключенной в объем тао:
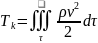 Полной
энергией называется сумма кинетической
и внутренней энергии данной массы газа:
Полной
энергией называется сумма кинетической
и внутренней энергии данной массы газа:

11. Выходит из закона сохранения энергии. Включает в себя внутреннюю энергию и кинетическую энергию в макродвижениях

 (4.1)
(4.1)
С точки зрения физики в внутреннюю энергию следует включить:
1)кинетическую энергию хаотического поступательного движения молекул.
2)кинетическую энергию хаотического вращательного движения молекул.
3)кинетическую энергию колебательного движения в молекулах.
4)энергию связей атомом в молекулах.(энергия диссоциации) 5)энергию связи электронной оболочки с ядром атома.(энергия ионизации)
6)энергию связи элементарной частицы в ядре атома
7)энергию потенциального взаимодействия между молекулами.
8)энергию взаимодействия с другими телами.
С точки зрения МЖГ во внутреннюю энергию следует включить лишь те состояния, которые изменяются с течением времени.
 ,
Т – энергия единицы массы. R
– газовая
постоянная сорта газа.
,
Т – энергия единицы массы. R
– газовая
постоянная сорта газа.

 (4.2)
(4.2)

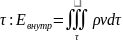 (4.3)
(4.3)
Билет №11
Внутренняя
энергия. Переход
массы жидкости из исходного положение
О в другое связано с изменением
 энергии. Будем считать что в исходном
состояние масса М имела запас энергии
.
Тогда можно ввести велечену
энергии. Будем считать что в исходном
состояние масса М имела запас энергии
.
Тогда можно ввести велечену
(1.1)
Если
известна величина
 , то ε может быть определена по формуле
(1.1).
, то ε может быть определена по формуле
(1.1).
Введем величину E – внутренняя энергия, отнесенная к единице массы. В общем случае неоднородной движущейся жидкости E – функция координат и времени:
 (1.2)
(1.2)
Из
определения (1.2) следует, что запас
внутренней энергии в массе dm
равен
 Внутренняя энергия в конечной массы
жидкости в объеме τ
Внутренняя энергия в конечной массы
жидкости в объеме τ
 (1.3)
(1.3)
Выражение
для внутренней энергии имеет вид
 ,
где
,
где
 - теплоемкость при постоянном объеме.
Когда нет процессов диссоциации и
ионизации, внутренняя энергия состоит
из энергии поступательного
- теплоемкость при постоянном объеме.
Когда нет процессов диссоциации и
ионизации, внутренняя энергия состоит
из энергии поступательного
 ,
вращательного
,
вращательного
 и колебательного
и колебательного
 движения молекул. Для одноатомного
газа
движения молекул. Для одноатомного
газа
 .
Для двухатомного, когда практически
возбуждены только поступательные и
вращательные энергии молекул, теплоемкость
постоянна и
.
Для двухатомного, когда практически
возбуждены только поступательные и
вращательные энергии молекул, теплоемкость
постоянна и
 .
При высоких температурах начинает
сказываться возбуждение колебательной
энергии молекул. Внутренняя энергия
может быть записана в виде
.
При высоких температурах начинает
сказываться возбуждение колебательной
энергии молекул. Внутренняя энергия
может быть записана в виде
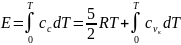 .
Зависимость
.
Зависимость
 от T
известна. Для многоатомных газов вид
функции
и
от T
будет зависеть не только от числа
атомов, но и от структуры молекул.
от T
известна. Для многоатомных газов вид
функции
и
от T
будет зависеть не только от числа
атомов, но и от структуры молекул.
Кинетической
энергии. Если
жидкость движется, то она обладает
кинетической энергией. Кинетическая
энергия
 массы dm,
движущейся со скоростью v,
равна
массы dm,
движущейся со скоростью v,
равна
 .
Кинетическая энергия массы заключена
в объем τ:
.
Кинетическая энергия массы заключена
в объем τ:
 (2.1)
(2.1)
Билет
№12 Вектор
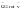 и его компоненты в декартовых координатах.
Связь
и его компоненты в декартовых координатах.
Связь
 с угловой скоростью вращения жидкой
частицы.
с угловой скоростью вращения жидкой
частицы.
Вектор
 и его компоненты в декартовых координатах.
Связь
и его компоненты в декартовых координатах.
Связь
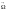 с угловой скоростью вращения жидкой
частицы.
с угловой скоростью вращения жидкой
частицы.
Уравнение
Эйлера в форме Громеки – Лэмба :

Запишем
уравнение в проекции на оси, используя
обозначение
 :
:

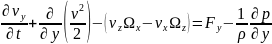

Здесь


Уравнение Громеки – Лэмба содержат в явном виде вектор вихря Ω.
Компоненты скорости есть частные производные от φ(x,y,z,t) по координатам. Функцию φ называют потенциалом скоростей.
12. Скорость любой точки жидкой частицы может быть представлена в виде

Где
 -
скорость полюса,
-
скорость полюса,
 -
чисто деформационная скорость,
-
чисто деформационная скорость,
 -скорость
точки во вращательном движении
затвердевшей жидкой частицы с угловой
скоростью
-скорость
точки во вращательном движении
затвердевшей жидкой частицы с угловой
скоростью
 .
.
Вектор Ω= rot v=2ω- удвоенная угловая скорость, с которой затвердевшая жидкая частица вращается вокруг оси, проходящей через полюс. Проекция вихря скорости
 =
= -
-
 = 2
= 2 ,
,
 =
= -
-
 = 2
= 2 ,
,
 =
= -
-
 = 2
= 2 .
.
Проекцию вектора угловой скорости на какую-либо ось можно одновременно рассматривать как угловую скорость вращения относительно этой оси. Поэтому проекция вихря скорости есть удвоенные угловые скорости, с которыми затвердевшая жидкая частица вращается вокруг осей, параллельных осям координат.
