1.3. Моделирование газового режима в литейной форме.

Организация направленного газового потока в форме от поверхности раздела отливка-форма является важным фактором, влияющим на качество отливки. При нарушении направленности потока, газы перемещаются в сторону отливки и внедряются в жидкий металл, что сопровождается эффектом вскипа, с последующим образованием газовых включений в отливке.

Условия создания направленного газового потока в форме выражается следующим соотношением давлений, действующих в порах формовочного материала:

Рф< Рм + Рп,

где Рф - избыточное давление в порах формовочного материала на границе металл-форма; Рм - металлостатический напор; Рп - давление, необходимое для преодоления пузырьками газа поверхностного сопротивления металла.

Критическая величина газопроницаемости, при которой сохраняется направленный газовый поток, зависит от многих факторов. В производственных условиях ее величина определяется опытным путем в каждом конкретном случае.

В литературе имеются формулы расчета газового давления в порах формы для отливок произвольной конфигурации. Эти формулы содержат геометрические характеристики области фильтрации газового потока ℓ. Методы вычисления F и ℓ для литейной формы не разработаны. Поэтому для отливок очень трудно точно рассчитать газовое давление в исследуемой точке и, следовательно, нельзя гарантировать, что газовое давление не будет превышать критического значения, при котором газ проникает из формы в металл.

Кроме того, реальные отливки заливаются в интервале времени. Так как конвейерное чугунное литье заливается в интервале 20-40 с, скорость газовыделения разных участков контакта металл-форма в этом случае отличается в 3-5 раз, а имеющиеся в литературе формулы оказываются непригодными даже для простейших отливок.

Электрическое моделирование газового режима литейных форм позволяет определить приведенную площадь Р и длину пути фильтрации газов ℓ и рассчитать по ним газовое давление в формах и стержнях произвольной конфигурации.

Плоскопараллельная фильтрация.

Изучение фильтрации проводилось в смеси, заформованной в кварцевую трубку диаметром d=55-65 мм путём заливки поверхности жидким металлом. Измерение газового давления в смеси производили U-образными водяными манометрами. Результаты приводят к расчетным формулам по определению максимального газового давления для конкретных значений F и ℓ.

Для облицовочной смеси при температуре заливки чугуна 1573 ± 15 К пересчет газового давления ведется по формуле

∆P0 max = 2*10ˉ²* y3*ℓ / F,

y3 = 1640-238*x1+212*x2-43*x3+171*x1*x2-79*x2*x3-80*x1²-185*x2²-30*x3²,

где Х1 - содержание песка 2К0315 в % по массе, остальное - песок 2К016; Х2 - глина в % по массе; Х3 - вода в % по массе.

Для сырой песчано-глинистой смеси с газопроницаемостью К=11,9*10мн/нс пересчет максимального газового давления ведется по формуле

∆P0 max = 20,23*10* y3*ℓ / F * К,

y4 = 740+30*x1+99*x2-39*x3+46*x4-123*(x1*x2+x3*x4)-41* (x1*x2-x2*x3)+135* * (x1*x3+x2*x4)+38*x1²+29*x2²+45*x3²-12*x4²,

где Х1- вода в % по массе; Х2- глина в % по массе; Хз- мазут в % по массе; Х4 - опилки в % по массе.

Методика электромоделирования.

Достаточное условие для моделирования условий фильтрации методом электроаналогии формулируется следующим образом:

1. Электрическая модель должна представлять изучаемую область

фильтрации в некотором масштабе без всякого искажения.

2. Коэффициенты электропроводности в модели должны быть пропорциональны соответствующим коэффициентам фильтрации.

3. Граничные условия для модели и натуры должны быть подобны, т.е. связаны между собой линейкой зависимостью

φ = a*P + в,

где φ - электрический потенциал; Р - давление газа; а, в - постоянные коэффициенты.

Рассмотрим возможность моделирования фильтрации в плоскости произвольной геометрии при мгновенной заливке. Пусть у нас есть трубка с размерами ℓ1 , F1 , Fk1 с известной величиной тазового давления в смеси ∆Р1 (при мгновенной заливке трубки металлом).

Уравнение Дарси для случая плоскопараллельной фильтрации в трубке с размерами ℓ1, F1, Fk1 и в области с произвольной геометрией ℓ, F, Fk запишется ввиде

υ1* Fk1=K*∆Р1*F1/ℓ; υ* Fk=K*∆Р1*F/ℓ,

где ℓ1 , ℓ - длина пути фильтрации газа; Fk1 , Fk - площадь контакта смеси с металлом; F1 , F - приведенная площадь фильтрации газового потока.

Скорость газовыделения равна скорости газоотвода при максимуме газового давления. В случае одинаковой площади контакта (Fk1= Fk), приравнивая два уравнения, получим

∆Р=ℓ*F1*∆Р1 / ℓ1* F= m*P1,

где m = ℓ*F / ℓ1*F1.

Таким образом, связь между газовым давлением при плоскопараялельной фильтрами и фильтрацией в плоскости произвольной геометрии при мгновенной заливке определяется соотношением геометрических величин, входящих в коэффициент m.

Граничные условия можно записать

φ= ∆Р1*m/ ∆Рmax = m * φ1,

т.e. как функцию газового давления при плоскопараллельной фильтрации.

Как результат электромоделирования фильтрации в плоскости получаем ряд эквипотенциалей, по которым строим трубки тока. Выделим одну из них в области интересующей точки на поверхности отливка-форма. Ось симметрии трубки тока является длиной пути фильтрации ℓ и определяется по чертежу. Разбивая общую длину фильтрации на участки ∆ ℓi, определяем для каждого участка приведенную площадь фильтрации Fi

Fi = π * (d i) ² /4,

где di - диаметр i -го участка трубки тока, определяемый как промежуток между нормалями к эквипотенциалям.

Число продиктовано требуемой точностью измерений. Величина Fk подсчитывается как площадь круга

Fk = π * (d ) ² /4,

где d - диаметр условной трубки тока в месте контакта смеси с металлом.

При моделирования задается потенциал отливки (по схеме рис.1.21, где 1 - электропроводная бумага, пропорциональная размеру формы; 2 -металлическая фольга, моделирующая сечение отливки; 3 - внешняя поверхность формы (электрический нуль - сток газов); 4 - щуп). Результаты моделирования можно представить в виде эквипотенциален (рис.1.22). Далее в окрестностях исследуемой точки выделяется площадь контакта Fk. Для каждой Fk можно построить трубки тока по найденным эквипотенциалям и определить для нее длину пути фильтрации ℓ, приведенную площадь фильтрации F и вычислить по ним газовое давление.

Если ограничиться построением трубки тока не на всю длину, а только на часть эквипотенциалей, расположенных в однородной области фильтрации, то тем самым снижается трудоемкость моделирования. Формула для вычисления избыточного газового давления участка по части трубки тока примет вид

∆Рi = φk*Fk*ℓx*∆Р1 / (φk-φx)*Fx*ℓ1,

где φk - потенциал формы для стержня в месте контакта; φx - потенциал эквипотенциали, до которой строится трубка тока; Fk - приведенная площадь фильтрации

Fx = (Fk - F) / 2.

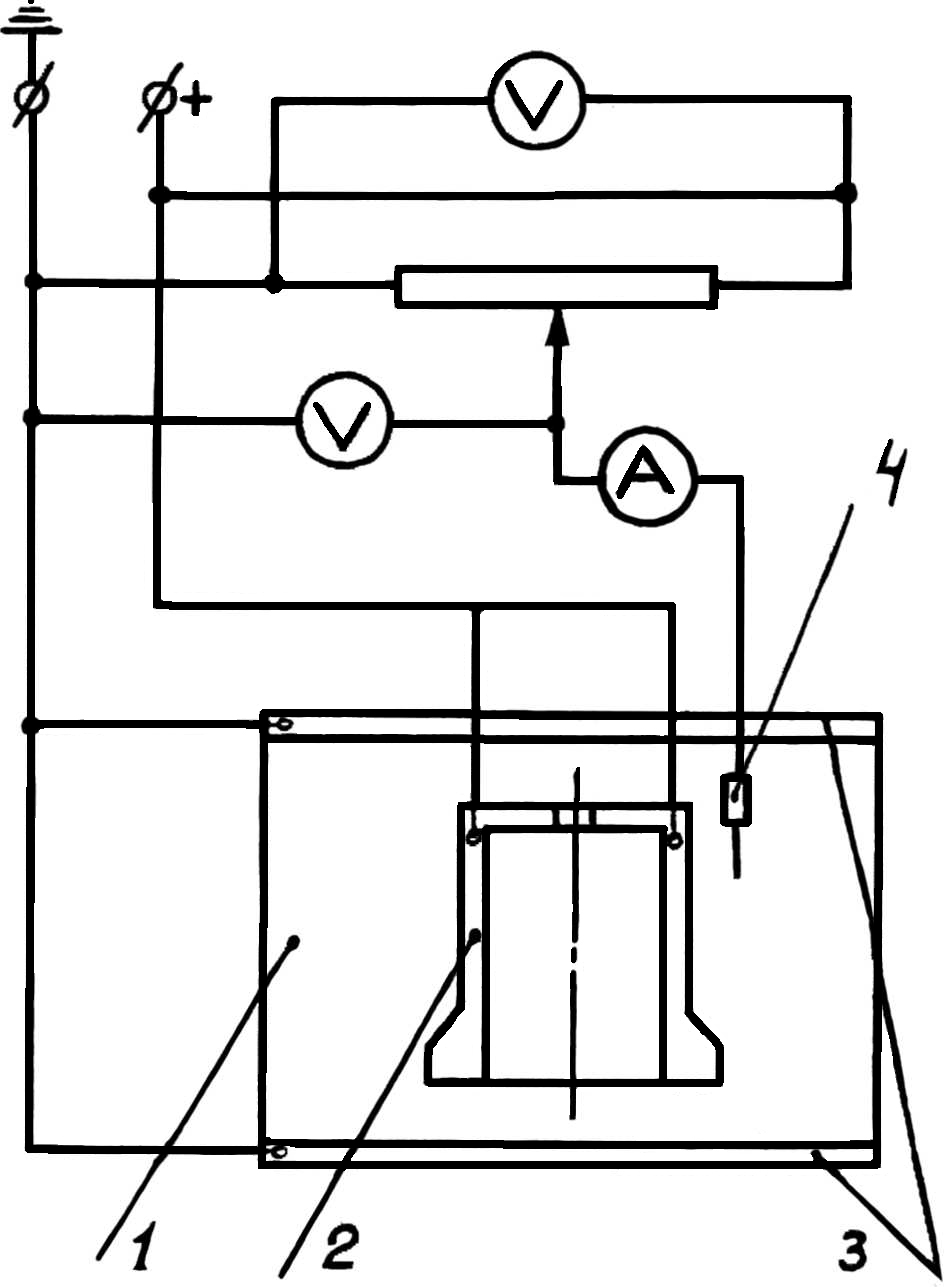
Рис.1.21. Схема задания исходных потенциалов.

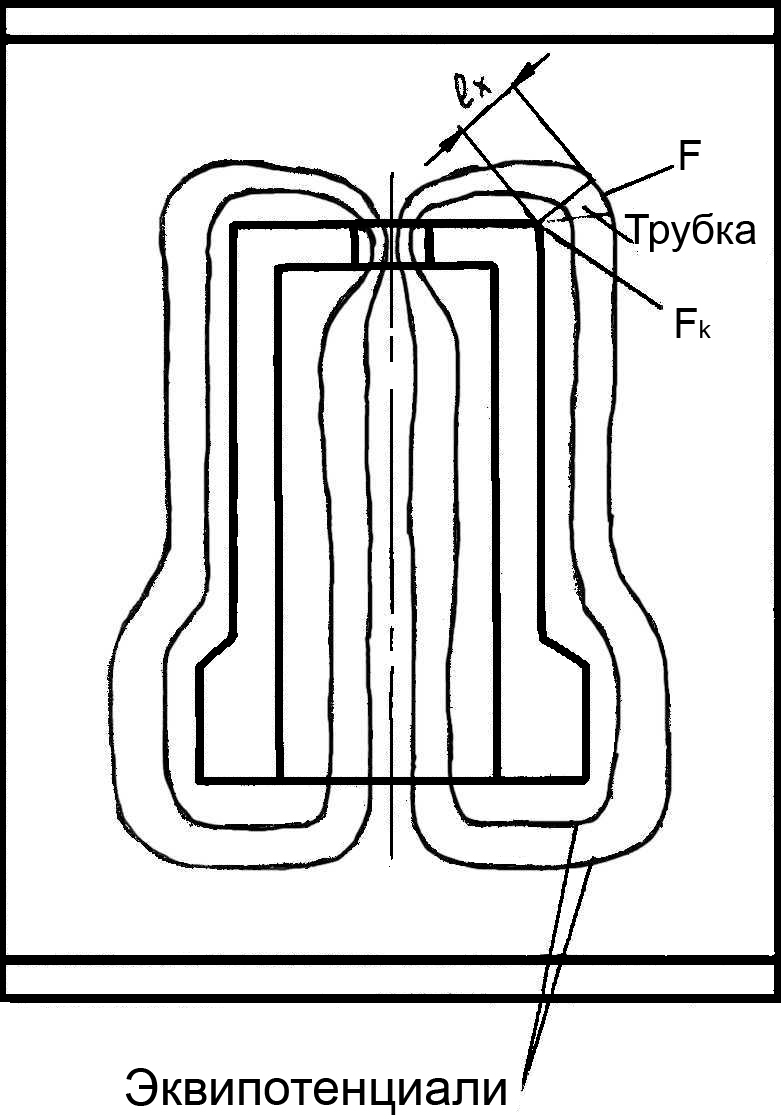
Рис.1.22. Измеренное распределение потенциала.