Изменение напряжений в металле и форме при совместной деформации.

Баланс усилий может произойти при определенной совместной деформации отливки и стержня.

Величину совместной деформации определяем методом (итерационным) последовательного приближения. Для этого общую границу раздела на опорной поверхности отливка - форма искусственно изменив ее перемещение.

При реализации перемещения в отливке отыскивается соответствующее ему распределение напряжений. В форме, в соответствии с новым положением границы раздела, определяется новое распределение напряжений.

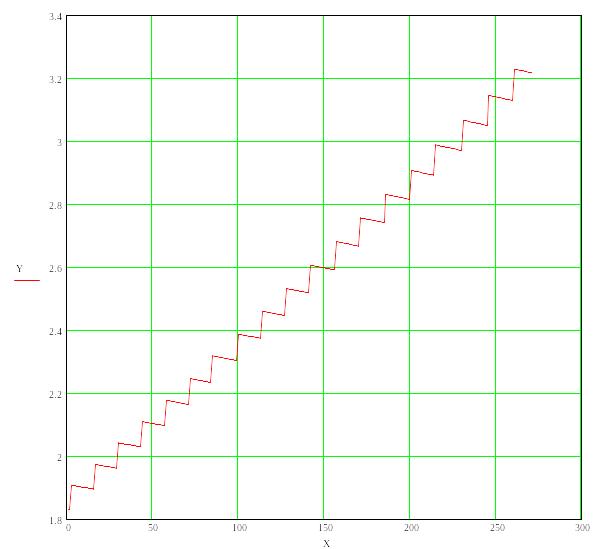
Рис.4.54. Выполнение условий баланса напряжений в отливке и форме.

Сравнение напряжений в материале отливки и формы часто показывают различие в этих значениях, что требует следующего шага увеличения деформации отливки (сокращения) и, соответственно, формы. При этом новом значении  определяются новые значения усилий в металле и стержне. Достижение близких значений усилий останавливает итерационный процесс, фиксируется полученная величина деформаций и напряжений, которая является равновесной для данного момента времени.

Перечисленный процесс повторяется для каждого текущего момента времени.

В результате имеем кинетику изменения напряженно-деформированного состояния отливки и формы. Проводя вычислительные эксперименты, можно оценивать опасность трещинообразования для различных конфигураций отливки при различных стержневых смесях.

Итоговое перемещение опорной поверхности

время перемещение среднее напряжение ЧИСЛО температура плотность упругость

в границы напряжение на границе итераций в форме в форме формы

с отливки в металле формы на упорной границе

в мм в МПа в МПа в град кг/м**3 МН/м**2

10.2 0.000050  0.0000 1.491 P= 1 930 1650.0 40.0

11.2 0.000100  0.0000 1.537 P= 1 956 1650.1 40.0

12.2 0.000150  0.0000 1.577 P= 1 979 1650.1 40.0

13.2 0.000200  0.0000 1.613 P= 1 999 1650.1 40.0

14.2 0.000250  0.0000 1.645 P= 1 1017 1650.2 40.0

15.2 0.000300  0.0000 1.674 P= 1 1033 1650.2 40.0

16.2 0.000350  0.0467 1.700 P= 1 1047 1650.2 40.1

17.2 0.000400  0.0933 1.724 P= 1 1060 1650.3 40.1

18.2 0.000450  0.1400 1.747 P= 1 1072 1650.3 40.1

19.2 0.000500  0.1867 1.767 P= 1 1083 1650.4 40.1

20.2 0.000550  0.2333 1.787 P= 1 1093 1650.4 40.1

21.2 0.000600  0.2800 1.805 P= 1 1102 1650.4 40.1

22.2 0.000650  0.3267 1.822 P= 1 1110 1650.5 40.1

23.2 0.000700  0.3733 1.838 P= 1 1118 1650.5 40.1

24.2 0.000750  0.4200 1.853 P= 1 1126 1650.5 40.1

25.2 0.000800  0.4667 1.868 P= 1 1132 1650.6 40.1

26.2 0.000850  0.5133 1.882 P= 1 1139 1650.6 40.1

27.2 0.000900  0.5600 1.895 P= 1 1145 1650.6 40.1

28.2 0.000950  0.6067 1.907 P= 1 1150 1650.7 40.1

29.2 0.001000  0.6533 1.919 P= 1 1156 1650.7 40.1

30.2 0.001050  0.7000 1.930 P= 1 1160 1650.8 40.2

31.2 0.001100  0.7467 1.940 P= 1 1164 1650.8 40.2

32.2 0.001150  0.7933 1.950 P= 1 1168 1650.8 40.2

33.2 0.001200  0.8400 1.960 P= 1 1172 1650.9 40.2

34.2 0.001250  0.8867 1.968 P= 1 1175 1650.9 40.2

35.2 0.001300  0.9333 1.976 P= 1 1178 1650.9 40.2

36.2 0.001350  0.9800 1.983 P= 1 1180 1651.0 40.2

37.2 0.001400  1.0267 1.989 P= 1 1182 1651.0 40.2

38.2 0.001450  0.6720 1.995 P= 1 1183 1651.0 40.2

39.2 0.001500  0.7280 2.000 P= 1 1184 1651.1 40.2

40.2 0.001550  0.7840 2.005 P= 1 1185 1651.1 40.2

41.2 0.001600  0.8400 2.009 P= 1 1185 1651.2 40.2

42.2 0.001650  0.8960 2.013 P= 1 1185 1651.2 40.2

43.2 0.001700  0.9520 2.017 P= 1 1185 1651.2 40.2

44.2 0.001750  0.8517 2.020 P= 1 1185 1651.3 40.3

45.2 0.001800  0.7900 2.023 P= 1 1185 1651.3 40.3

46.2 0.001850  0.8500 2.026 P= 1 1184 1651.3 40.3

47.2 0.001900  0.9100 2.029 P= 1 1184 1651.4 40.3

48.2 0.001950  0.9700 2.031 P= 1 1183 1651.4 40.3

49.2 0.002000  1.0300 2.034 P= 1 1182 1651.5 40.3

50.2 0.002050  1.0900 2.036 P= 1 1182 1651.5 40.3

51.2 0.002100  0.9100 2.039 P= 1 1181 1651.5 40.3

52.2 0.002150  1.0033 2.041 P= 1 1180 1651.6 40.3

53.2 0.002200  1.1122 2.044 P= 1 1179 1651.6 40.3

54.2 0.002250  1.2367 2.046 P= 1 1178 1651.6 40.3

55.2 0.002300  1.3611 2.048 P= 1 1178 1651.7 40.3

56.2 0.002350  1.4856 2.050 P= 1 1177 1651.7 40.3

57.2 0.002400  1.6100 2.053 P= 1 1176 1651.8 40.4

58.2 0.002450  1.7344 2.055 P= 1 1175 1651.8 40.4

59.2 0.002500  1.8589 2.057 P= 1 1174 1651.8 40.4

60.2 0.002550  1.9833 2.059 P= 1 1173 1651.9 40.4

61.2 0.004550  2.1984 2.203 P= 40 1172 1653.4 40.7

62.2 0.007350  2.3993 2.402 P= 56 1171 1655.4 41.1

63.2 0.010200  2.5993 2.601 P= 57 1170 1657.4 41.5

64.2 0.013100  2.7984 2.801 P= 58 1169 1659.5 41.9

65.2 0.016000  2.9976 2.998 P= 58 1168 1661.5 42.3

66.2 0.018950  3.1958 3.196 P= 59 1167 1663.4 42.7

67.2 0.021950  3.3931 3.395 P= 60 1166 1665.4 43.1

68.2 0.024950  3.5904 3.590 P= 60 1165 1667.4 43.5

69.2 0.028000  3.7869 3.787 P= 61 1164 1669.3 43.9

70.2 0.031100  3.9824 3.985 P= 62 1164 1671.2 44.2

71.2 0.034200  4.1780 4.180 P= 62 1163 1673.1 44.6

72.2 0.037350  4.3727 4.377 P= 63 1162 1675.0 45.0

73.2 0.040500  4.5673 4.571 P= 63 1161 1676.9 45.4

74.2 0.043650  4.7620 4.763 P= 63 1160 1678.7 45.7

75.2 0.046850  4.9558 4.957 P= 64 1159 1680.5 46.1

76.2 0.050100  5.1487 5.152 P= 65 1158 1682.4 46.5

Определение деформационных свойств формы выполняется путем сличения кривой деформации, полученной на модели и кривой деформации, полученной экспериментально.

Для этого нужен специальный алгоритм с неполным экспериментальным материалом.

После определения свойств формы можно выполнять расчет деформации отливок для конкретных случаев.