6.2 Соединение трехфазной цепи звездой. Четырех- и трехпроводная цепи

Р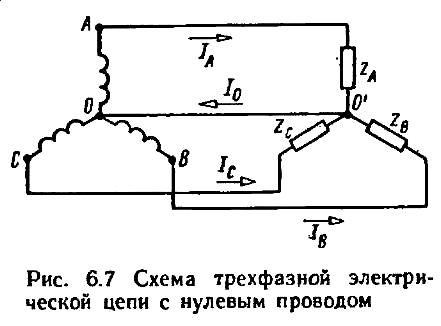 ассмотрим соединение генератора с нагрузкой, включенной звездой (рис. 6.5).

Рисунок 6.5 Схема трехфазной электрической цепи с нулевым проводом

Провод 00' называют нулевым (четырехпроводная цепь). В соответствии с первым законом Кирхгофа вектор тока в нулевом проводе

Как отмечалось, при симметричной нагрузке, когда сопротивления , и равны между собой и имеют одинаковый характер, векторы токов , , равны по абсолютному значению и образуют трехлучевую звезду, у которой углы между лучами равны 120°.

Из геометрического построения, показанного на рис. 6.8, следует, что в этом случае векторная сумма токов равна нулю:

Р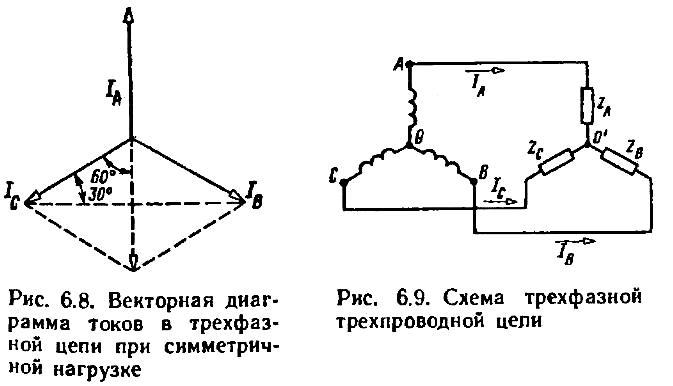 исунок 6.6 Векторная диаграмма токов в трехфазной цепи при симметричной нагрузке и схема трехфазной трехпроводной цепи

Таким образом, при симметричной нагрузке нулевой провод не нужен. Получается схема трехфазной трехпроводной цепи, изображенная на рис. 6.6.

Площадь поперечного сечения нулевого провода принимают равной половине площади поперечного сечения каждого из остальных трех проводов (их сечения равны между собой).

6.3 Соотношения между фазными и линейными напряжениями и токами при симметричной нагрузке в трехфазной цепи соединенной звездой

Система ЭДС обмоток трехфазного генератора, работающего в энергосистеме, всегда симметрична: ЭДС поддерживаются строго постоянными по амплитуде и сдвинутыми по фазе на 120°.

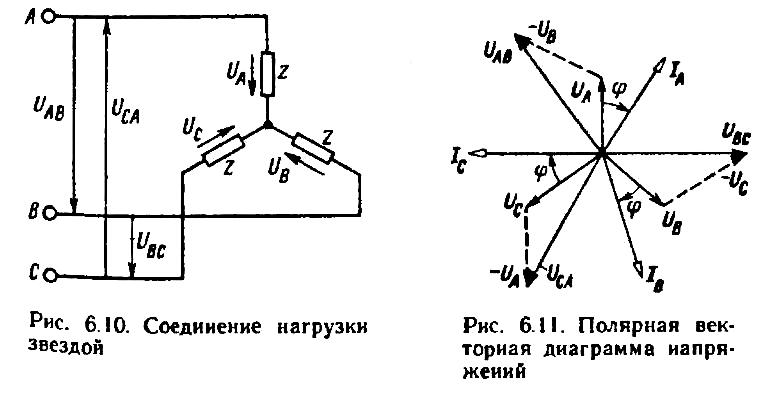
Рассмотрим симметричную нагрузку (рис. 6.7), для которой

, .

Рисунок 6.7 Соединение нагрузки звездой и ее полярная векторная диаграмма

К зажимам А, В, С подходят провода линии электропередачи — линейные провода.

Введем обозначения: — линейный ток в проводах линии электропередачи; — ток в сопротивлениях (фазах) нагрузки; — линейное напряжение между линейными проводами; — фазное напряжение на фазах нагрузки.

В рассматриваемой схеме фазные и линейные токи совпадают: , напряжения , и являются линейными, а напряжения , , — фазными. Складывая напряжения, находим (рис. 6.10):

, , .

Векторную диаграмму, удовлетворяющую этим уравнениям (рис. 6.7), начинаем строить с изображения звезды фазных напряжений , , . Затем строим вектор — как геометрическую сумму векторов и , вектор — как геометрическую сумму векторов и , вектор — как геометрическую сумму векторов и

Для полноты картины на векторной диаграмме изображены также векторы токов, отстающих на угол φ от векторов соответствующих фазных напряжений (нагрузку считаем индуктивной).

На построенной векторной диаграмме начала всех векторов совмещены в одной точке (полюсе), поэтому ее называют полярной. Основное достоинство полярной векторной диаграммы — ее наглядность.

У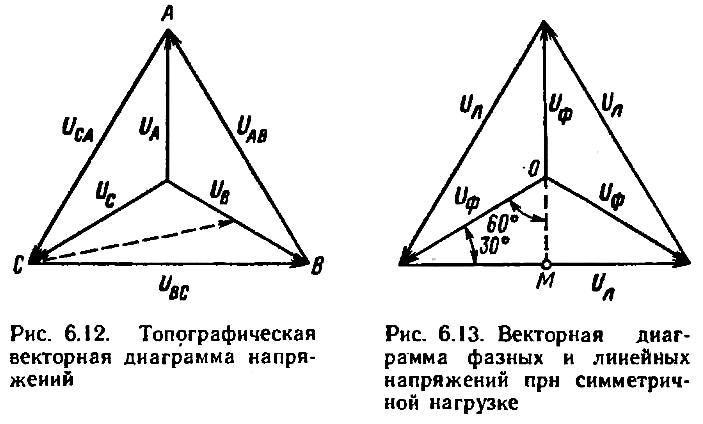 равнениям, связывающим векторы линейных и фазных напряжений, удовлетворяет также векторная диаграмма рис. 6.8, которую называют топографической. Она позволяет графически найти напряжение между любыми точками схемы, изображенной на рис. 6.7. Например, для определения напряжения между точкой С и точкой, которая делит пополам сопротивление, включенное в фазу В, достаточно соединить на векторной диаграмме точку С с серединой вектора . На диаграмме вектор искомого напряжения показан пунктиром.

Рисунок 6.8 Топографическая векторная диаграмма напряжений и векторная диаграмма фазных и линейных напряжений при симметричной нагрузке

При симметричной нагрузке модули векторов фазных (и линейных) напряжений равны между собой. Тогда топографическую диаграмму можно изобразить так, как показано на рис. 6.8.

Опустив перпендикуляр ОМ, из прямоугольного треугольника находим

В симметричной звезде фазные и линейные токи и напряжения связаны соотношениями , .