3.13 Эдс самоиндукции. Энергия магнитного поля
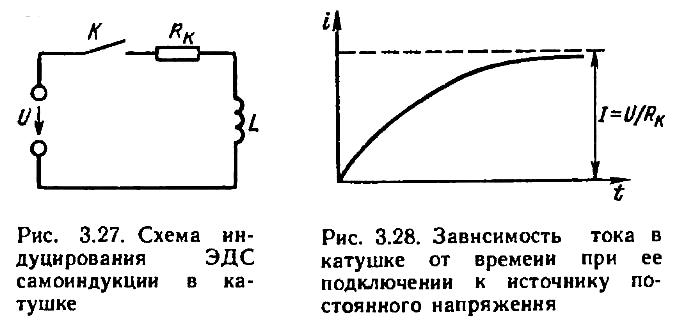
Рассмотрим процесс,
происходящий в цепи (рис. 3.19) при замыкании
ключа К. До замыкания ключа ток в цепи
I=0.
После замыкания ключа ток в цепи
устанавливается не мгновенно и лишь
через определенное время достигает
значения
.
Следовательно, ток, проходящий через
катушку, изменяется, а значит, изменяется
поток
каждого витка и потокосцепление катушки
.
Согласно (3.15), в каждом витке наводится
ЭДС
,
а во всей катушке ЭДС
.
Рисунок 3.19 Схема индуцирования ЭДС самоиндукции в катушке
Выражение в скобках
представляет собой сумму производных
и может быть заменено производной суммы
потоков
:
.
В соответствии с (3.21)
. Но
и для катушки без ферромагнитного
сердечника (L=const) окончательно получим
(3.24)
ЭДС
называют ЭДС самоиндукции, а рассмотренное
явление возникновения ЭДС в катушке
вследствие изменения тока в этой катушке
— самоиндукцией.
ЭДС самоиндукции,
согласно принципу Ленца, препятствует
изменению тока в катушке, поэтому ток
достигает установившегося значения
постепенно (рис. 3.20). Если замкнуть
катушку на резистор, то ток в цепи не
исчезает мгновенно, так как ЭДС
самоиндукции препятствует его уменьшению.
Прохождение тока через
сопровождается выделением тепловой
энергии, что свидетельствует о накоплении
энергии в магнитном поле катушки. Найдем
значение этой энергии. Согласно второму
закону Кирхгофа для цепи рис. 3.19,
,
откуда
,
т. Е. падение напряжения источника
частично происходит на
и частично у
равновешивает
ЭДС самоиндукции
.
Рисунок 3.20 Зависимость тока в катушке от времени при ее подключении к источнику постоянного напряжения
Умножим последнее уравнение на idt:
где
— энергия, которую отдает источник в
цепь за время dt;
— энергия, выделяемая в виде теплоты
на резисторе
;
— энергия, накапливаемая в магнитном
поле катушки за время dt.
Для нахождения всей энергии, которая накопится в магнитном поле катушки при изменении тока от 0 до , проинтегрируем выражение для :
(3.25)
Это выражение
аналогично выражению для кинетической
энергии тела массой М, движущегося со
скоростью v.
.
Глава 4. Основные понятия переменного тока
4.1 Определение, получение и изображение переменного тока
Переменным называют ток, изменение которого по значению и направлению повторяется через равные промежутки времени.
Широкое применение переменного тока в различных областях техники объясняется легкостью его получения и преобразования, а также простотой устройства генераторов и двигателей переменного тока, надежностью их работы и удобством эксплуатации. Рассмотрим принцип действия простейшего генератора переменного тока.
Между полюсами электромагнита или постоянного магнита (рис. 4.1) расположен цилиндрический ротор (якорь), набранный из листов электротехнической стали. На якоре укреплена катушка, состоящая из определенного числа витков проволоки. Концы этой катушки соединены с контактными кольцами, которые вращаются вместе с якорем.
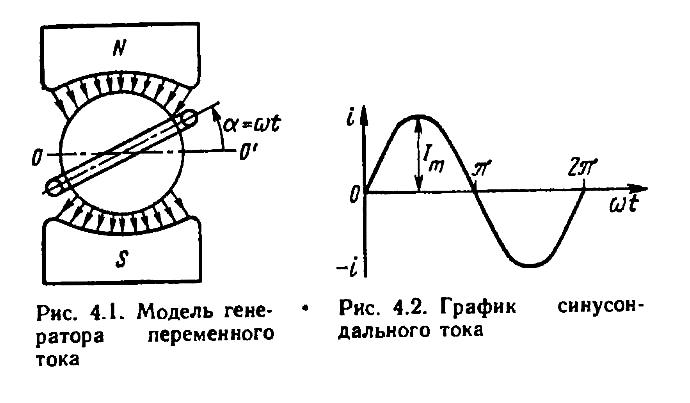
Рисунок 4.1 Модель генератора переменного тока
С контактными кольцами связаны неподвижные контакты (щетки), с помощью которых катушка соединяется с внешней цепью. Воздушный зазор между полюсами и якорем профилируют так, чтобы индукция магнитного поля в нем менялась по синусоидальному закону:
,
где α— угол между плоскостью катушки и нейтральной плоскостью 00'.
Когда якорь вращается в магнитном поле со скоростью о), в активных сторонах катушки наводится ЭДС индукции (активными называют стороны, находящиеся в магнитном поле генератора)
,
где β — угол между направлениями векторов индукции магнитного поля В и скорости v; l — длина активных сторон витков катушки.
Магнитное поле в
зазоре расположено так, что угол
.
Таким образом,
.
При числе витков w число активных сторон катушки равно 2w. Тогда ЭДС катушки
(4.1)
Где
— максимальное значение ЭДС.
Таким образом, ЭДС
генератора меняется по синусоидальному
закону. Если к зажимам генератора
подключить нагрузку, то через нее пойдет
ток, который также будет изменяться по
синусоидальному закону. График
синусоидального тока
представлен на рис. 4.2. По оси ординат
откладывают ток i, по оси абсцисс — угол
или время t.
Рисунок 4.2 График синусоидального тока