Тесты по теории вероятностей

1. Случайное событие – это событие,

А) причины которого неизвестны;

+) которое при совокупности одних и тех же условий может произойти, а может не произойти;

В) если условия, в которых оно происходит, различны;

Г) закономерности которого не поддаются наблюдению.

2. Если два события не могут произойти одновременно, то они называются:

А) невозможными;

Б) совместными;

В) независимыми;

+) несовместными.

3. Отношением числа случаев, благоприятствующих событию A, к числу всех возможных случаев называется:

+) вероятность;

Б) математическое ожидание;

В) число сочетаний;

Г) число размещений.

4. Если событие обязательно происходит при каждом испытании, то оно называется:

А) невозможным;

+) достоверным;

В) случайным;

Г) независимым.

5. Как называются два события, если непоявление одного из них влечёт появление другого?

+) противоположные;

б) несовместные;

в) равносильные;

г) совместные.

6. Укажите математическую запись теоремы сложения вероятностей:

А) P (A и B) = P(A) + P(B);

+) P (A или B) = P(A) + P(B);

В) P(A)+P(B)=1;

Г) P(A)+P(B)=0.

7. Укажите математическую запись теоремы умножения вероятностей:

А) P(A)·P(B)=0;

Б) P (A или B) = P(A) · P(B);

В) P(A)·P(B)=1;

+) P (A и B) = P(A) · P(B).

8. По какой формуле вычисляется вероятность противоположного события , если известна вероятность P(A) события A?

А) ;

+) ;

В) ;

Г) .

9. Укажите формулировку теоремы сложения вероятностей:

А) сумма вероятностей наступления случайного события A и противоположного ему события Ā равна 1.

Б) вероятность наступления случайного события А и зависящего от него события В равна сумме вероятности события А и условной вероятности события В.

+) вероятность появления какого-либо события из нескольких несовместных событий равна сумме их вероятностей;

Г) вероятность совместного появления независимых событий равна сумме их вероятностей.

10. Укажите формулировку теоремы умножения вероятностей:

А) вероятность появления какого-либо события из нескольких несовместных событий равна произведению их вероятностей;

+) вероятность совместного появления независимых событий равна произведению их

вероятностей;

В) произведение вероятностей наступления случайного события A и противоположного ему события Ā равна 1;

Г) произведение вероятностей наступления случайного события A и противоположного ему события Ā равна 0.

11. Если m – это количество элементарных событий, благоприятствующих событию A, а n – общее количество элементарных событий, то вероятность события A равна:

А) ;

+) ;

В) ;

Г) .

12. Укажите диапазон значений, которые может принимать вероятность произвольного случайного события А:

+) 0  P(A)  1;

Б) 0 < P(A) < 1;

В) 1  Р(А)  100;

Г) -1 < P(A) < 1;

13. Вероятность достоверного события равна:

А) 0;

Б) 0,5;

+) 1;

Г) зависит от условий испытания.

14. Сумма вероятностей наступления случайного события A и противоположного ему события Ā равна:

А) 0;

Б) 0,5;

+) 1;

Г) зависит от условий испытания.

15. Случайной величиной называется величина:

А) принимающая в результате испытания числовое значение, которое можно предсказать при большом числе испытаний;

+) принимающая в результате испытания числовое значение, которое принципиально нельзя предсказать, исходя из условий испытания;

В) которая принимает только счетное множество значений;

Г) которая принимает только значения внутри некоторого интервала.

16. Дискретной случайной величиной называется величина:

А) принимающая в результате испытания числовое значение, которое можно предсказать при большом числе испытаний;

Б) принимающая в результате испытания числовое значение, которое принципиально нельзя предсказать, исходя из условий испытания;

+) которая принимает счетное множество значений;

Г) которая принимает любые значения внутри некоторого интервала.

17. Непрервыной случайной величиной называется величина:

А) принимающая в результате испытания числовое значение, которое можно предсказать при большом числе испытаний;

Б) принимающая в результате испытания числовое значение, которое принципиально нельзя предсказать, исходя из условий испытания;

В) которая принимает счетное множество значений;

+) которая принимает любые значения внутри некоторого интервала.

18. Укажите формулу для определения математического ожидания дискретной случайной величины:

А)

Б)

-+)

+-)

19. Укажите формулу для определения математического ожидания непрерывной случайной величины:

+)

Б)

В)

Г)

20. Укажите формулу для определения дисперсии непрерывной случайной величины:

А)

Б)

В)

+)

21. Укажите формулу для определения дисперсии дискретной случайной величины:

А)

+)

В)

Г)

22. Какие значения может принимать функция плотности вероятности непрерывной случайной величины:

А) любые положительные значения;

Б) от 0 до 1;

+) любые неотрицательные значения;

Г) от -1 до 1.

23. Какие значения может принимать функция распределения случайной величины:

А) любые неотрицательные значения;

+) от 0 до 1;

В) любые положительные значения;

Г) от -1 до 1.

24. Функция распределения любой случайной величины есть функция:

+-) неубывающая;

+-) убывающая;

В) невозрастающая;

Г) возрастающая.

25. Нормальное распределение имеет вид:

А) ;

Б) ;

+) ;

Г) .
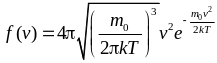