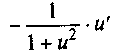Основные теоремы о непрерывных функциях.
Алгебраическая сумма конечного числа непрерывных функций в некотором промежутке есть функция, непрерывная в этом промежутке.
Произведение конечного числа непрерывных функций в некотором промежутке есть функция, непрерывная в этом промежутке.
Отношение двух функций, непрерывных в некотором промежутке, является непрерывной функцией во всех точках этого промежутка, в которых знаменатель отличен от нуля.
Если функции f(x) и g(x) непрерывны в своих областях определения и область значений функции g(x) содержится в области определения функции f(x), то сложная функция φ(x)=f(g(x)) непрерывна в своей области определения.
Непрерывность элементарных функций.
Каждая из элементарных функций непрерывна в любой точке, в которой она определена.
Свойства функций, непрерывных на отрезке.
Теорема 1. Если непрерывная на отрезке [a,b] функция принимает на концах этого отрезка значения А и В, то на этом отрезке она принимает и все промежуточные значения между А и В.
Следствие. Если функция f(x) непрерывна на отрезке [a,b] и на его концах принимает значения разных знаков, то существует хотя бы одна точка с в интервале (a,b), в которой f(x)=0
Теорема 2. Если функция f(x) непрерывна на отрезке [a,b], то она достигает на этом промежутке своего наибольшего и наименьшего значения.
Тема 1.5. Производная функции. Понятие производной
Производная функции f в точке х0 есть скорость изменения функции f в этой точке.
Геометрическое толкование производной. Производная функции f в точке х0 определяется тангенсом угла наклона касательной, проведённой к графику функции f в точке х0.
Операцию получения функции
из
функции f(x)называют
дифференцированием функции f(x).
Основные правила дифференцирования
Производная постоянной равна нулю, т.е.
Производная аргумента равна 1. т.е.
В следующих правилах будем
полагать, что
и
- дифференцируемые функции.
Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, т.е.
4. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е.
Следствие 1. Постоянный множитель можно выносить за знак производной:
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные, например:
5. Производная частного двух дифференцируемых функций может быть найдена по формуле
Таблица производных
-
№
Функция у
Производная
У
№
Функция у
Производная
У'
1
с
0
13
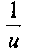
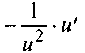
2
x
1
14
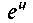
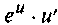
3
u+v
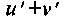
15
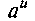
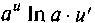
4
uv
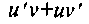
16
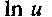
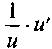
5
uvw
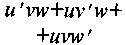
17
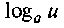
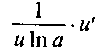
6
сu
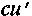
18
sin u
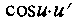
7
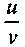
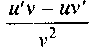
19
cos u
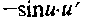
8
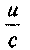
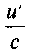
20
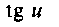
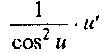
9
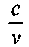
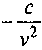
21
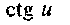
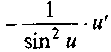
10
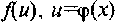
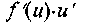
22
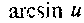
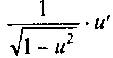
11
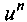
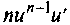
23
arccos u
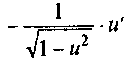
12
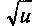
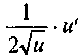
24
arctg u
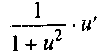
25
arcctg u
