Бесконечно малые величины.

Определение. Функция (х) называется бесконечно малой величиной при хх₀, или при х , если ее предел равен нулю:

.

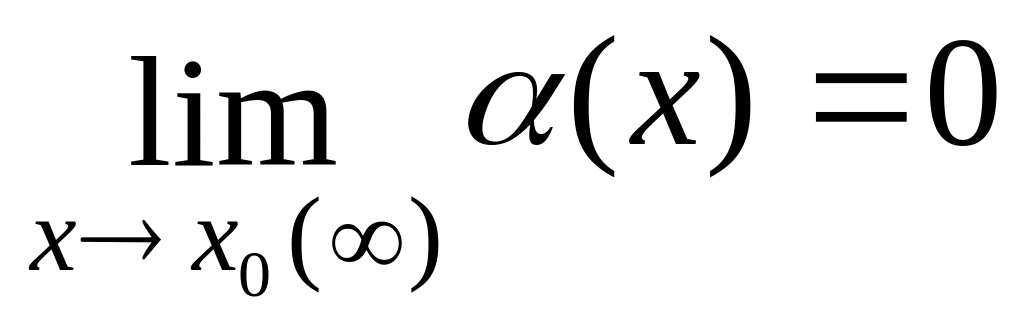Зная определение предела функции при хх₀ и при х можно дать развернутое определение бесконечно малой величины:

Функция а(х) называется бесконечно малой величиной при хх_0,если для любого, даже сколь угодно малого положительного числа >0, найдется такое положительное число  >0 (зависящее от , =())), что для всех х, неравных х₀ и удовлетворяющих условию |х-х₀| <  (****) будет верно неравенство |(х)| <  (*****)

Аналогично можно сформулировать определение бесконечно малой при x, если основное неравенство (*****) рассматривать для достаточно больших х. Приводим его в краткой форме:

Свойства бесконечно малых величин:

1. Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.

2. Произведение бесконечно малой величины на ограниченную функцию (в том числе на постоянную, на другую бесконечно малую) есть величина бесконечно малая.

3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.

Бесконечно большие величины.

Определение. Функция f(x) называется бесконечно большой величиной при х х_0, если для любого, даже сколь угодно большого положительного числа M > 0, найдется такое положительное число >0 (зависящее от М, =(M)), что для всех х, не равных х₀ и

удовлетворяющих условию |х—х₀| < , будет верно неравенство

|f(x)| > M.

Это означает, что функция f(x) является бесконечно большой величиной при х х₀, если

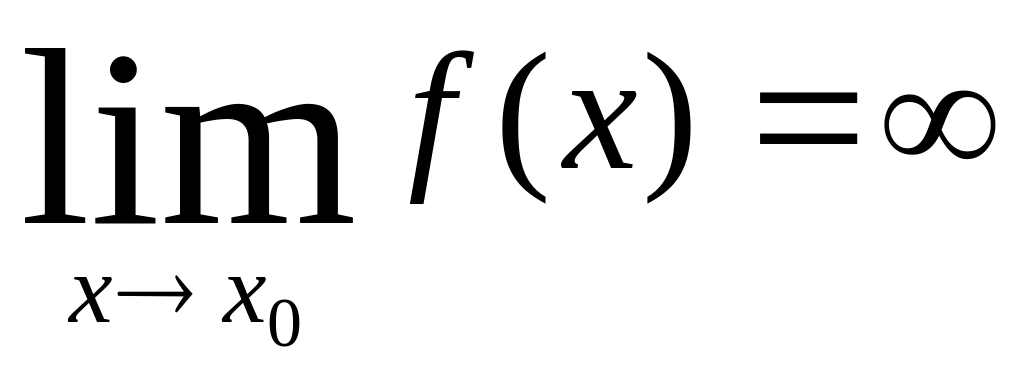
Свойства бесконечно больших величин:

1. Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.

2. Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.

3. Частное от деления бесконечно большой величины на функцию, имеющую предел в точке х₀, есть величина бесконечно большая.

Связь между бесконечно малыми и бесконечно большими величинами.

Теорема. Если функция (х) есть бесконечно малая величина при х х₀ (), то функция является бесконечно большой при х х₀ ().

Обратное утверждения тоже верно.

Свойства пределов.

1. Функция не может иметь более одного предела

2. Если функции f(x) и g(x) определены в некоторой окрестности тачки a, возможно за исключением самой точки а, и существуют пределы 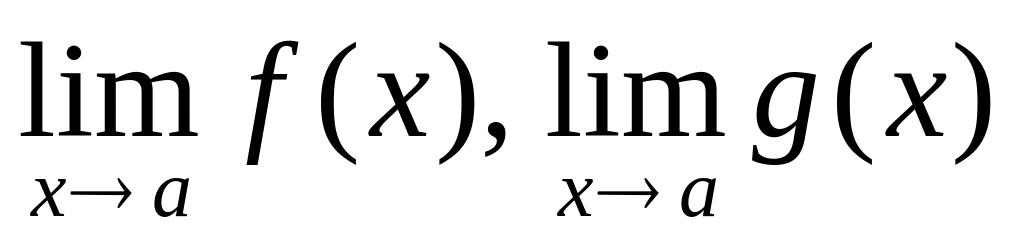, то существуют пределы их алгебраической суммы, произведения и, если g(x)≠0, 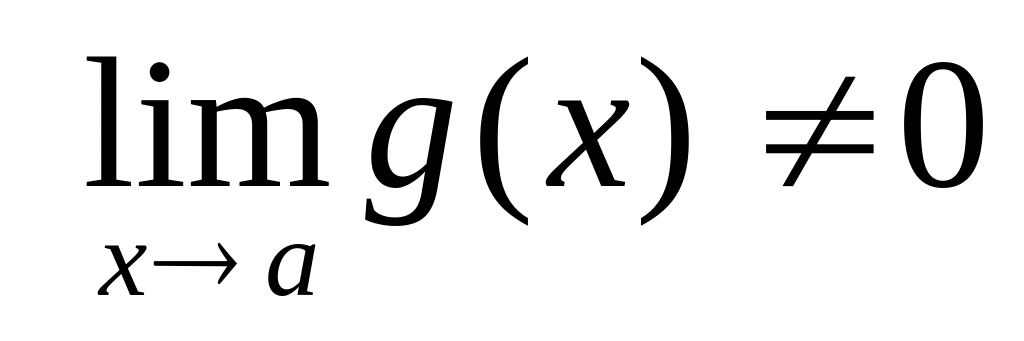, то и частного и имеют место равенства:

   1. 

   2. 

   3. 

3. Предел постоянной величины равен самой постоянной.

4. Постоянный множитель можно выносить из-под знака предела.

5. Предел степени равен степени предела.

Замечательные пределы.

Первый замечательный предел:

Второй замечательный предел:

, где  2,718281…

Число е – число Эйлера, неперово число

Тема 1.4. Непрерывность функции. Определение непрерывности функции. Точки разрыва.

Определение 1. Функция f(x) называется непрерывной в точке х=х₀, если она определена в некоторой окрестности точки х₀ (следовательно, и в самой точке х₀), существует предел функции при х→х₀ и он равен значению функции в этой точке:

Определение 2. Функция называется непрерывной на некотором промежутке, если оно непрерывна в каждой точке этого промежутка.

Определение 3. Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.

Определение 4. Если правый (левый) предел совпадает со значением функции, то функция называется непрерывной справа (слева) в рассматриваемой точке.

Определение 5. Точка разрыва функции называется точкой разрыва первого рода, если в ней функция имеет конечные левый и правый пределы. Все остальные точки разрыва называются точками разрыва второго рода.