Свойства функции

1. Функция y = f(x) называется четной, если для любого значения х из области определения f(-x) = f(x) и нечетной, если f(-x) = -f(x). В противном случае функция общего вида.

2. График четной функции симметричен относительно оси ординат, а график нечетной функции относительно начала координат

3. Функция называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.

4. Функция f(x) называется ограниченной на Х, если существует такое положительное число M > 0, что |f(x)| ≤ M для любого

5. Функция y = f(x) называется периодичной с периодом T 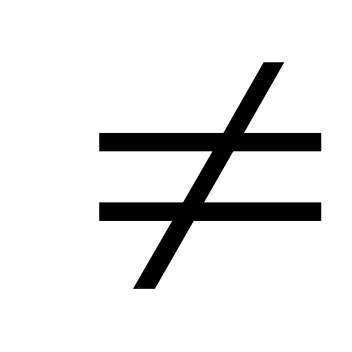0, если для любого Х из области определения функции f(x+T) = f(x)

6. Функция y = f(x) называется выпуклой вниз на промежутке Х, если для любых двух значений х₁, х₂ 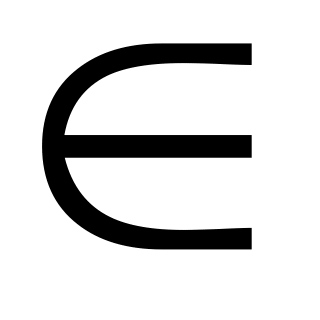Х из этого промежутка выполняется неравенство

7. Функция называется выпуклой вверх на промежутке Х, если для любых двух значении х₁, х₂ Х из этого промежутка выполняется неравенство

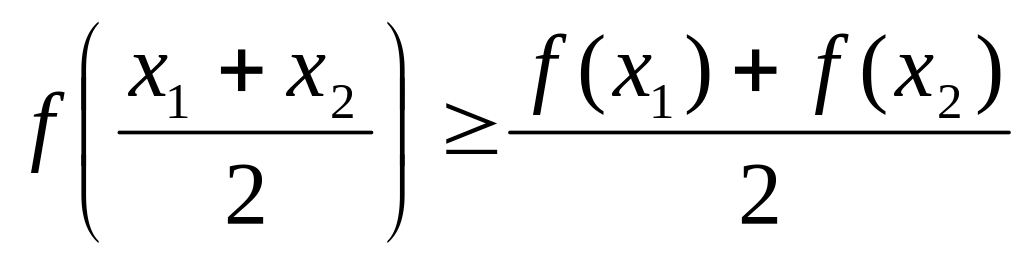
Тема 1.3. Предел функции. Предел функции на бесконечности.

Определение. Число А называется пределом функции у = f(x) при х, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа >0, найдется такое положительное число S >0 (зависящее от ; S=S()), что для всех х таких, что |x|>S, верно неравенство

| f(x)-а|<. (*)

Этот предел функции обозначается или при

С помощью логических символов определение имеет вид:

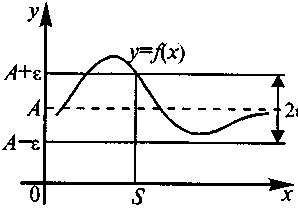
Выясним геометрический смысл предела функции у= f(x) в бесконечности. Неравенство (*) |f(x)-А|< равносильно двойному неравенству A—<f(x)< А+, соответствующему расположению части графика в полосе шириной 2(см. рис. 1).

Итак, число А есть предел функции y=f(x) при х, если для любого >0 найдется такое число S>0, что

Рис. 1 для всех х таких, что |x|>S, соответствующие ординаты графика функции f(x) будут заключены в полосе A—<f(x)< А+, какой бы узкой эта полоса ни была.

Предел функции в точке.

Пусть функция y=f(x) задана в некоторой окрестности точки х₀, кроме, быть может, самой точки х₀.

Определение. Число А называется пределом функции f(x) при х, стремящемся к х₀ (или в точке х₀ ), если для любого, даже сколь угодно малого положительного числа >0, найдется такое положительное число >0 (зависящее от , =()), что для всех х, не равных x₀ и удовлетворяющих условию

|х-х₀|<, (**)

выполняется неравенство

|f(x)-А|< (***)

Этот предел функции обозначается или при

С помощью логических символов определение имеет вид:

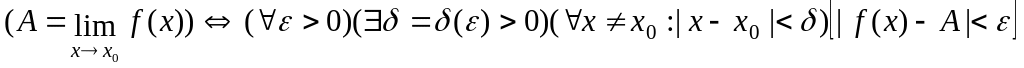
Смысл определения предела функции f(x) в точке х₀ состоит в том, что для всех значений х, достаточно близких к х₀, значения функции f(x) как угодно мало отличаются от числа А (по абсолютной величине).

Р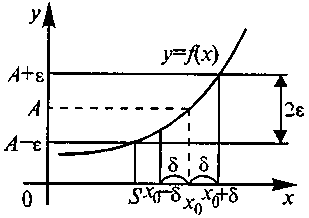 ассмотрим геометрический смысл предела функции в точке. Как отмечалось выше, неравенство |f(x)-А|< равносильно двойному неравенству A—<f(x)< А+, соответствующему расположению части графика в полосе шириной 2(см. рис.2.). Аналогично |х-х₀|< неравенство равносильно двойному неравенству х₀-<x< х₀+,

Рис. 2 соответствующему попаданию точек х в -окрестностъ точки х₀.