4. Эквивалентность и порядок.

Рассмотренные ниже отношения представляют собой формально определенные типы отношений, отличающиеся фиксированным набором свойств.

Отношением эквивалентности (или просто эквивалентностью) называют бинарное отношение на множестве, если оно рефлексивно, симметрично, транзитивно. Например, отношение "жить в одном городе" на множестве людей - эквивалентность.

Отношение эквивалентности имеет важную особенность: эквивалентность R разбивает множество М, на котором оно задано, на непересекающиеся подмножества так, что элементы одного и того же подмножества находятся в отношении R, а между элементами из разных подмножеств отношение R отсутствует. В таком случае говорят, что отношение R задает разбиение на множестве М, или систему классов эквивалентности по отношению R. Мощность этой системы называется индексом разбиения. В то же время любое разбиение множества М на классы определяет некоторое отношение эквивалентности, а именно отношение "входить в один и тот же класс данного разбиения".

Отношением нестрогого порядка (или нестрогим порядком) называют бинарное отношение на множестве, если оно рефлексивно, антисимметрично, транзитивно, и отношением строго порядка (строгим порядком), если оно антирефлексивно, антисимметрично, транзитивно. Оба эти отношения называются отношениями порядка. Например, отношения "быть не старше" на множестве людей, "быть не больше" на множестве натуральных чисел - нестрогий порядок; отношения "быть моложе", "быть прямым потомком" на множестве людей - строгий порядок.

Элементы а,b M сравнимы по отношению порядка R на М, если выполняется a R b или b R a.

Множество М, на котором задано отношение порядка, может быть:

а) полностью упорядоченным множеством, если любые два элемента из М сравнимы по отношению порядка. В таком случае говорят, что отношение R задает полный порядок на множестве М. Например, отношение "быть не старше" задает полный порядок на множестве людей;

б) частично упорядоченным множеством - в противном случае. При этом говорят, что отношение R задает на множестве М частичный порядок. Например, отношение "быть начальником" задает на множестве сотрудников организации частичный порядок, так как, например, для пары сотрудников одного отдела данное отношение не выполняется: они не сравнимы по данному отношению.

Пример 11.

К каким типам отношений относятся следующие отношения?

1) отношение равносильности на множестве формул, описывающих элементарные функции (формулы равносильны, если они задают одну и ту же функцию, например (а + b) (а - b) = a²- b², sin²  + cos²  = 1);

2) отношение, определяемое на множестве всех программ {(а, b): а и b вычисляют одну и ту же функцию на определенной машине};

3) отношения  и < на множестве векторов длины п с ко­понентами из N, определяемые следующим образом:

а) (а₁,..., а_п) (b₁,..., b_п), если а₁  b₁,..., а_n  b_n;

б) (а₁,..., а_п)< (b₁,..., b_п), если (а₁,..., а_п) (b₁,..., b_п) и хотя бы в одной координате i выполняется а_i < b_i;

 Отношения, заданные в п. 1 и 2, являются отношениями эквивалентности на соответствующих множествах; отношения, заданные в п. 3, являются отношениями порядка; при этом отношение , определенное в п. 3, есть отношение нестрого порядка, а отношение < в п. 3, - отношение строго порядка.

Пример 12.

Проиллюстрируйте диаграммой Венна следующие разбиения множества U:

а) {А, ¬А};

б) {А  В, А  ¬В, ¬ А  В, ¬A  ¬B};

в){А\В, АВ, В\А}.

 Указанные разбиения изображены на рис.7.

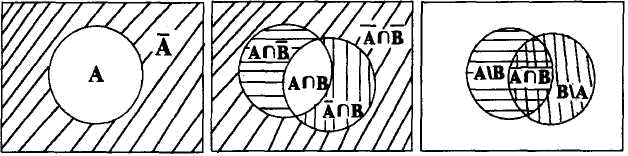
а) б) в)

Рис..7

Пример 13

Определите индекс разбиения и мощности классов эквивалентности по отношению R, если R:

1) отношение равенства (тождества) на любом множестве;

2) универсальное (полное) отношение на любом множестве;

3) отношение равносильности на множестве формул;

4) отношение "иметь один и тот же остаток от деления на 5" на множестве натуральных чисел N?

 1) Все классы эквивалентности по отношению равенства (тождества) Е = {(a, b): a = b} на любом множестве М, a,b M, состоят из одного элемента. Индекс разбиения М по отношению Е равен мощности множества М, т.е. |М|.

2) Индекс разбиения универсального (полного) отношения U, U= {(a, b): a U b для любых а,b  М}, т.е. U = M  M для любого М, равен единице. Все элементы множества M принадлежат одному классу эквивалентности по отношению U. Мощность класса равна |М|.

3) Формулы, описывающие одну и ту же элементарную функцию, находятся в одном классе эквивалентности по отношению равносильности. Поэтому счетны само множество формул, множество классов эквивалентности (индекс разбиения) и каждый класс эквивалентности. (Счетными множествами называются множества, равномощные N- множеству натуральных чисел.)

4) Индекс разбиения множества N по заданному отношению R равен 5. Множества натуральных чисел, составляющие каждый класс эквивалентности, - счетны.

Пример 14

Какой порядок на множестве задают отношения?

1)  и , а также < и > для чисел множеств N и R;

2)  и < на R, введенные в примере 11;

3)  и  на системе подмножеств (M) множества М;

4) подчиненности на предприятии.

 1) Отношения нестрого порядка  и , а также строго порядка < и > полностью упорядочивают множества M и R.

2) Отношения  и < на множестве векторов длины п с компонентами из R определяют частичный порядок на Rⁿ: (-3,3/5,2) > (-3,1/2,2); (-3,1/2,2) и (-3,2,1/2) - не сравнимы.

3) Отношение  на системе (M) задает строгий частичный порядок, а отношение ; - нестрогий частичный порядок. Например, {а, b}  {а, b, с}, но {а, b} и {b, с, d} несравнимы по отношению .

4) Отношение подчиненности на предприятии задает строгий частичный порядок. В нем несравнимыми являются, например, сотрудники разных звеньев одного уровня организационной структуры.