Лекция 2. Элементы теории множеств бинарные отношения. Основные определения

1. Отношения.

2. Бинарные отношения. Основные определения.

3. Свойства бинарных отношений.

4. Эквивалентность и порядок.

1. Отношения

Отношения - один из способов задания взаимосвязей между элементами множества. Наиболее изученными и чаще всего используемыми являются так называемые унарные и бинарные отношения.

Унарные (одноместные) отношения отражают наличие какого-то определенного признака R (свойства и т.п.) у элементов множества М (например, "быть белым" на множестве шаров в урне). Тогда все такие элементы а из множества М, которые отличаются данным признаком R, образуют некоторое подмножество в М, называемое унарным отношением R, т.е. а  R и R  М.

Бинарные (двухместные) отношения используются для определения каких-то взаимосвязей, которыми характеризуются пары элементов в множестве М (так, на множестве людей могут быть заданы, например, следующие бинарные отношения: "жить в одном городе", "быть моложе", "быть сыном", "работать в одной организации" и т.п.). Тогда все пары (а, b) элементов из М, между которыми имеет место данное отношение R, образуют подмножество пар из множества всех возможных пар элементов ММ= М², называемое бинарным отношением R, т.е. (a, b)  R, при этом R  М  М.

В общем случае могут рассматриваться п-местные отношения, например отношения между тройками элементов - трехместные (тернарные) отношения и т.д.

Под п-местным отношением понимают подмножество R прямого произведения п множеств: R  М₁  М₂  ...  М_п. Говорят, что элементы а₁, а₂, … a_п (a₁  М₁, a₂  М₂, … a_n  М_n) находятся в отношении R, если (а_1, а₂ ..., а_п)  R. Если n-местное отношение R задано на множестве М своих элементов, т.е. М₁ = М₂ = ... = М_n, то R  М_n.

2. Бинарные отношения. Основные определения.

Двухместным, или бинарным, отношением R называется подмножество пар (а, b)  R прямого произведения М₁  М₂, т.е. R  М₁  М₂. При этом множество М₁ называют областью определения отношения R, множество М₂ - областью значений. Часто рассматривают отношения R между парами элементов одного и того же множества М, тогда R  М  М. Если a, b находятся в отношении R, это часто записывается как а R b.

Пусть R  А  В определено в соответствии с изображением на рис.1. Область определения D(R) и область значении Q(R) определяются соответственно:

D(R) = {а: (а, b)  R}, Q(R) = {b: (a, b)  R}.

Рис.1

Способы задания бинарных отношений - любые способы задания множеств (так как отношения определены выше как подмножества некоторых множеств - прямых произведений). Отношения, определенные на конечных множествах, обычно задаются:

1. Списком (перечислением) пар, для которых это отношение выполняется.

Пример 1.

R = {(а, b), (а, с), (b, d)}.

2. Матрицей - бинарному отношению R  М  М, где М = {а_1, а₂ ..., а_п}, - соответствует квадратная матрица порядка n, в которой элемент с_ij, стоящий на пересечении i-й строки и j-го столбца, равен 1, если между а и а имеет место отношение R, или 0, если оно отсутствует:

Пример 2.

Пусть М- {1,2,3,4,5,6}. Задайте в явном виде (списком) и матрицей отношение

R  M  M, если R означает "быть строго меньше".

Отношение R как множество содержит все пары элементов a, b из М такие, что а < b:

R = {(a,b): a,bM; a<b}. Тогда:

R = {(1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 5), (4, 6), (5, 6)}.

a) б) в) г)

Рис.2

Пример 3.

Пусть М- {1,2,3,4, 5,6}. Составить матрицы отношения R_1, R₂, R₃  M M, если:

1) R₁ - "быть делителем";

2) R₂- "иметь общий делитель, отличный от единицы";

3) R₃- "иметь один и тот же остаток от деления на 3".

1) R₁ = {(а, b}): а,b  М; а - делитель b} и выполняется для пар {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (5, 5), (6, 6)}. Эти пары (a, b)  R₁, определяют наличие единиц в матрице отношения R₁M² на пересечении строки элемента а и столбца элемента b; а,b М (рис.2. б);

2) R₂ = {(а, b): a, b  М; а и b имеют общий делитель, с  1}. Матрица отношения R₂ представлена на рис.2. в):

3) R₃ = {(a, b): a,b  M; a, b имеют один и тот же остаток от деления на 3}. Матрица отношения R₃ приведена на рис.2. г).

Пример 4.

Для указанных ниже отношений привести примеры пар, для которых выполняются отношения, и пар, для которых отношения не выполняются.

1. Отношения, заданные на множестве точек действительной плоскости:

а) R₁- "находиться на одинаковом расстоянии от начала координат";

б) R₂ -"находиться на разном расстоянии от начала координат";

в) R₃ - "находиться на одной и той же окружности с центром в начале координат";

г) R₄ - "быть симметричным относительно оси X.

2. Отношения, заданные на множестве элементов структуры, изображенной на рис.3;

а) R₅ - "быть частью целого";

б) R₆ - "быть непосредственно связанным с";

в) R₇ - "быть начальником";

г) R₈ - "быть непосредственным начальником".

Рис.3

3. Отношения, заданные на системе множеств (M), М={а,b,с}:

а) R₉ - "пересекаться с" (иметь непустое пересечение);

б) R₁₀ - "являться строгим включением  ";

в) R₁₁ - "являться нестрогим включением  ";

г) R₁₂ - "быть дополнением к".

 Примеры пар элементов с отношениями между ними и без таковых приведены в табл.1.

1.Отношения, заданные на множестве точек действительной плоскости.

Отношения R_l и R₃ равны и выполняются (не выполняются) для одних и тех же пар точек.

Таблица 1

Отношение	Примеры пар, для которых отношение
	выполняется	не выполняется
1. Отношения, заданные на множестве точек действительной плоскости: R1- "находиться на одинаковом расстоянии от начала координат"	((3, 4), (-3, 4)), ((3, 4), (0, -5))	((3,4), (1,6))
R2- "находиться на разном расстоянии от начала координат"	((3,4), (1,6))	((3, 4), (-3, 4)), ((3, 4), (0, -5))
R3- "находиться на одной и той же окружности с центром в начале координат"	((3, 4), (-3, 4)), ((3, 4), (0, -5))	((3, 4), (1,6))
R4 — "быть симметричным относительно оси X"	((3, 4), (3, -4)), ((-3, 4), (-3, -4)	((3,4), (-3,4)), ((3, 4), (-3, -4))
2. Отношения, заданные на множестве элементов структуры (рис.3): R5- "быть частью целого"	(b, a), (d, а), (с, а)	(d.f),(a.b),(g,b)
R6- "быть непосредственно связанным с"	(d, b), (b, d), (с, а)	(d,f),(g,b),(d,a}
R7- "быть начальником"	(b, d), (a, d), (а, с)	(d, b),(b, g)
R8- "быть непосредственным начальником	(b, d), (a, b)	(d, b), (a, d), (b, g)
3. Отношения, заданные на системе множеств (М), М= {а, b, с}: R9- "пересекаться с" (иметь не пустое пересечение)	({а}, (а, с}}, ({а, с}, {а,b}) ({а, с}, {а,b,с})	({a}, (b}), ({a},{b,c})
R10- "являться строгим включением  "	({а}, {а,с}) ({а, с}, {а,b,с})	({a,c}, {a,b}) ({a,c}, {a,c}) ({a}, {b,c})
R11- "являться нестрогим включением  "	({а}, (а, с}), ({а, с}, {а,b,с}), ({а, с}, {а, с})	({a.c}, {a,b}) ({a},{b,c})(d,f),(g,b),(d,a}
R12- "быть дополнением к"	({а},{b,с}), (, (а, b, с}}	({a}, (a, c}), ({a, b}, (a, c}).

Отношение R₂ выполняется для тех и только тех пар точек, для которых не выполняются предыдущие отношения R₁ и R₃

Отношение R₄ выполняется для всех пар точек (x_1,y_i) и (x_2,y₂), удовлетворяющих условию: x_l = х_2, у₁ = —у₂ и не выполняется в противном случае.

2. Отношения, заданные на множестве элементов структуры.

Рисунок 3 отражает связи между элементами, задающими отношения.

Структура, задающая отношение R₅, свидетельствует о том, что целое а состоит из двух частей: b и с, которые в свою очередь разделены на части d, e,f и g, h соответственно.

Отношение R₆ выполняется лишь для пар элементов, непосредственно связанных между собой линией.

Структура, задающая отношения R₇ и R₈, определяет начальника а, которому непосредственно подчинены b и с; в свою очередь, каждый из них имеет своих непосредственных подчиненных: d, e,f и g, h, соответственно.

3. Отношения, заданные на системе множеств(M),М= {а,b,с}.

Отношение R₉ выполняется для тех и только тех пар множеств из (M, которые содержат хотя бы один общий элемент из М.

Отношение R_l0 выполняется лишь для пар множеств, второе из которых содержит все элементы первого и по крайней мере, еще один, не содержащийся в первом.

Отношение R₁₁ выполняется для тех пар подмножеств, для которых выполняется отношение R₁₀, а также для пар одинаковых подмножеств.

Отношение R₁₂ выполняется для пар непересекающихся множеств, содержащих элементы, вместе составляющие (без повторов) множество М.

Пример 5.

Составьте матрицы отношений, заданных на системе множеств(М), М={а, b, с}:

1) R - "пересекаться с" (иметь непустое пересечение);

2) - "являться строгим включением ".

 (М) = (, {а}, {b}, {с}, {а, b}, (а, с}, {b, с}, {а, b, с}}. Матрицы отношений R_l и R₂ представлены на рис.4.

R1		{a}	{b}	{c}	{a,b}	{a,c}	{b,c}	{a,b,c}
	0	0	0	0	0	0	0	0
{a}	0	1	0	0	1	1	0	1
{b}	0	0	1	0	1	0	1	1
{c}	0	0	0	1	0	1	1	1
{a,b}	0	1	1	0	1	1	1	1
{a,c}	0	1	0	1	1	1	1	1
{b,c}	0	0	1	1	1	1	1	1
{a,b,c}	0	1	1	1	1	1	1	1

R2		{a}	{b}	{c}	{a,b}	{a,c}	{b,c}	{a,b,c}
	0	1	1	1	1	1	1	1
{a}	0	0	0	0	1	1	0	1
{b}	0	0	0	0	1	0	1	1
{c}	0	0	0	0	0	1	1	1
{a,b}	0	0	0	0	0	0	0	1
{a,c}	0	0	0	0	0	0	0	1
{b,c}	0	0	0	0	0	0	0	1
{a,b,c}	0	0	0	0	0	0	0	0

Рис.4

Пример 6.

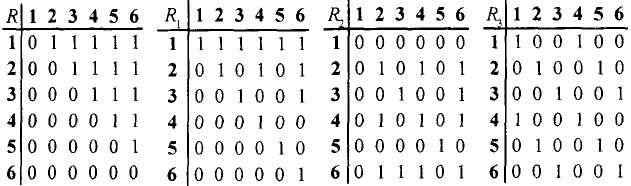
Для отношений, определенных на множестве М= {а, b, с, d, e, f, g, h} элементов структуры (см. рис.3), составьте матрицы:

1) R₁ - "быть частью целого";

2) R₂ - "быть непосредственно связанным с".

 Матрицы отношений R₁ и R₂ приведены на рис.5. (При построении матрицы отношения R₁ предполагалось, что "целое есть часть самого себя"; аналогично при построении матрицы отношения R₂.)

R1		a		b		c		d		e		f		g	h
a		1		0		0		0		0		0		0	0
b		1		1		0		0		0		0		0	0
c		1		0		1		0		0		0		0	0
d		1		1		0		1		0		0		0	0
e		1		1		0		0		1		0		0	0
f		1		1		0		0		0		1		0	0
g		1		0		1		0		0		0		1	0
h		1		0		1		0		0		0		0	1

R2	a	b	c	d	e	f	g	h
a	1	1	1	0	0	0	0	0
b	1	1	0	1	1	1	0	0
c	1	0	1	0	0	0	1	1
d	0	1	0	1	0	0	0	0
e	0	1	0	0	1	0	0	0
f	0	1	0	0	0	1	0	0
g	0	0	1	0	0	0	1	0
h	0	0	1	0	0	0	0	1

Рис.5

Пример 7.

Пусть отношение R - "быть отцом", определенное на множестве людей М = {а, b, с, d, e, f, g, h}, представлено схемой рис.3. Задать списком отношение R. Определите (назовите) родственные отношения между следующими парами: (a, b), (a, d), (b, с), (b, d), (b, h), (с, d).

 1) R = {(a, b), (a, c), (b. d), (b, e), (b,f), (c, g), (c, h)} -"быть отцом".

2) a - отец для b; a - дед для d; b - родной брат для с; b -отец для d; b - дядя для h; с - дядя для d.

В целом заданная матрица отношения R - "быть отцом" -позволяет установить новые отношения между элементами множества М, в том числе:

R₁ = {(a, d), (a, е), (a,f), (a, g), (a, h)} - "быть дедом";

R₂= {(b, с), (с, b), (d, e), (e, d), (d, f), (f,d), (e, f), (f,е), (g, h), (h, g)} - "быть родным братом или сестрой";

R₃ = {(d,g), (g, d), (d,h), (h,d), (e, g), (g, e), (e, h), (h, e), (f,g), (g,f), (f, h), (h,f)} -"быть двоюродным братом или сестрой";

R₄ ⁼ {(b, g), (b, h), (c, d), (с, е), (с,f)} - "быть дядей";

R₅ = {(g, b), (h, b), (d, c), (e, с), (f, с)} - "быть племянником или племянницей";

R₆ = {(b, a), (с, a), (d, b), (e, b), (f, b) (g, с), (h, с)} - "быть сыном или дочерью".

Уточним потомков b и с. Пусть d и g- дочери, e,f и h-сыновья для b и с соответственно. Тогда:

R₇ = {(b, с), (с, b), (e,f)б (f, e)} - "быть родным братом" (очевидно, что R₇  R₂;

R₈ = {(b, а), (с, a), (e, b), (f, b), (h, с)} - "быть сыном" (очевидно, что R₈  R₆).

R₉ = {(d,c), (g,b)} - "быть племянницей" (R₉  R₅) и т.д.