Міністерство освіти і науки України.

КНУБА

Кафедра інженерної геодезії

Практична робота №2

З геодезії

На тему: «Попередні обчислення в тріангуляції

Загальні відомості»

Виконав:

ст. гр. ГД-31

Захарченко Р.М.

Викладач: Шудра Н. С.

Київ 2014р.

Перед початком зрівнювання тріангуляції необхідно виміряні та зрівняні на станціях напрямки зприести до центрів знаків, редукувати їх на рефернц-еліпсоїд, а потім на площину в проекції Гаусса-Крюгера. Крім того, необхідно впевнитись, шо результати вимірювань не містять недопустимих помилок та за їх точністю відповідають вимогам.

У рівнинній та пагорбкуватій місцевості поправки у виміряні напрямки за редукцію до референц-еліпсоїда дуже малі, тому на пунктах 2- 4 класів їх не обчислюють. Однак у гірський місцевості, де цими поправками не можна знехтувати, їх необхідно обчислювати та враховувати.

Вихідні сторони, виміряні між центрами знаків та приведені до поверхні референц-еліпсоїда, необхідно також редукувати на площину. Від геодезичних азимутів вихідних сторін, заданих на поверхні референц- еліпсоїда, необхідно перейти до дирекційних кутів на площині.

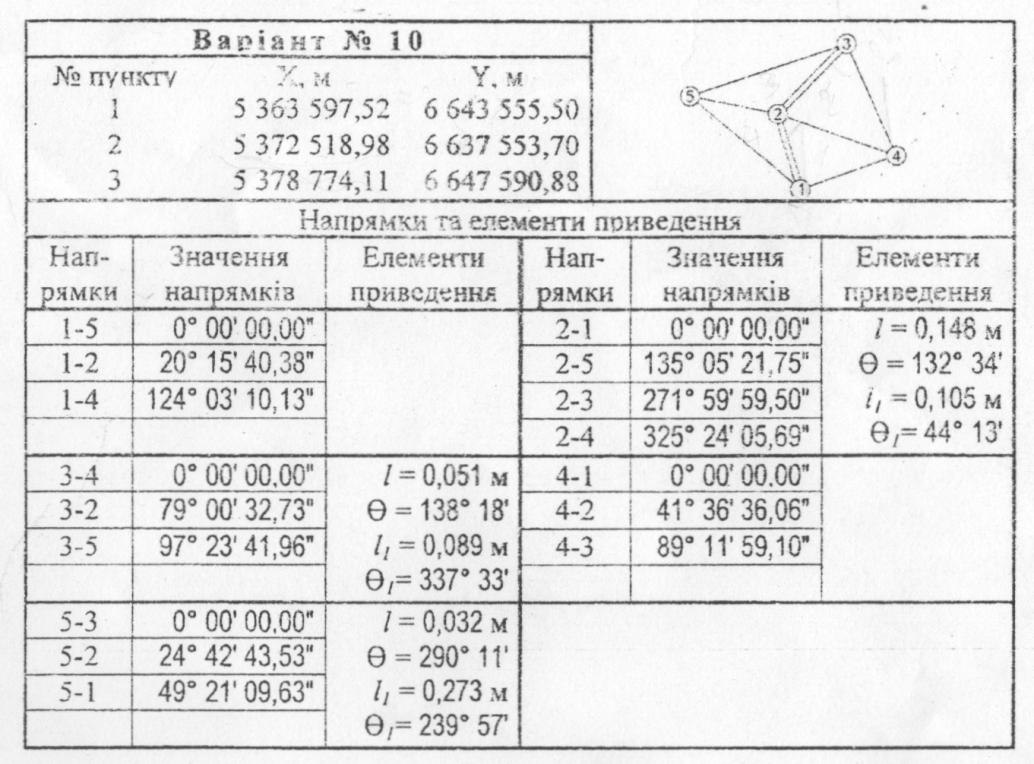
Попереднє вирішення трикутників та обчислення сферичних надлишків Для того, щоб обчислити поправки у виміряні напрямки за центрування теодоліта та редукції візирних цілей, необхідно знайти спочатку довжини сторін трикутників. Паралельно з вирішенням трикутників обчислюють їхні сферичні надлишки.

формули	і	1	2
	к	2	3
1		2	3
Xi		5363597,52	5372518,98
Xk		5372518,98	5378774,11
UX		8921,46	6255,13
Yi		6643555,5	6637553,7
Yk		6637553,7	6647590,88
UY		-6001,8	10037,18
tan r		-0,6727374	1,6046317
r		-0,5921937	1,0134954
α, рад		5,6909916	1,0134954
sin α		-0,5581825	0,8486857
cos α		0,8297182	0,5288975
S1		10752,397	11826,734
s2		10752,397	11826,734
α°		326,0701085	58,0690608

Попереднє вирішення трикутників та обчислення сферичних надлишків

№ трикутника	№ вершини	кути, °			кути, рад	Sin кутів	Довжина сторін, м	Сторони	Сферичні надлишки, ε
		°	'	"
1							28298	f=	0,00253
	3	18	23	9	0,3208933	0,3154144	8926	2=5	0,182
	2	136	54	37	2,3895351	0,6831428	19332	3=5
	5	24	42	14	0,4311642	0,4179287	11827	3=2
2							16018		0,378
	3	79	0	32	1,3789652	0,9816568	15724	2=4
	4	47	35	22	0,8305925	0,7383311	11827	3=2
	2	53	24	6	0,9320349	0,8028348	12860	4=3
3							25781		0,171
	5	24	38	57	0,4302091	0,4170609	10752	2=1
	2	135	5	22	2,3577556	0,7060021	18202	5=1
	1	20	15	41	0,3536279	0,3463035	8928	2=5
4							16192		0,243
	2	34	35	54	0,6038548	0,5678198	9194	4=1
	4	41	36	36	0,7262315	0,6640567	10752	2=1
	1	103	47	30	1,8115063	0,9711690	15725	2=4

При вирішенні трикутників намагаються притримуватись таких рекомендацій:

9. виділити на схемі мережі ланцюг послідовного вирішення трикутників та пронумерувати їх по порядку; трикутники, що не попадають в цей ланцюг, нумеруються та вирішуються останніми;

10. в кожному трикутнику на першому місці вписується номер вершини того кута, який лежить проти вихідної сторони, а на останньому – проти сторони, що є вихідною для вирішення наступного трикутника; кути виписуються з точністю до 1" так, щоб сума кутів у трикутнику була рівною точно 180°;

протилежні кути та сторони трикутника записують у кожному рядку

У трикутнику з виміряними кутами А, В, С довжини протилежних сторін обчислюють за теоремою синусів:

Прийнявши одну сторону за вихідну, інші обчислюються шляхом множення величини q на синус протилежного кута. Довжини сторін обчислюють до цілого міліметра:

Сферичний надлишок

де сторони а, b виражають в кілометрах;

Обчислення поправок за центрування та редукцію Як правило, на пункті тріангуляції проекції точки Л стояння теодоліту, візирної цілі знака 5 та його центра С на горизонтальну площину не співпадають між собою. Елементи центрувань та редукцій зазвичай малі та визначаються графічним способом. Проте в практиці геодезичних робіт зустрічаються випадки, коли лінійні елементи центрувань або редукцій дуже великі для графічних визначень (більше 0,2-0,3 м). В таких випадках вони визначаються аналітичними методами.

Отже, всі виміряні в точці І напрямки для приведення до центра знака в точці С повинні бути виправлені поправками с" за центрування теодоліта. Ці поправки додають зі своїми знаками до виміряних на даному пункті напрямків JA, JB і т.д. (рис. 2). Поправки ^а редукцію візирної цілі 5 даного пункту вводяться зі своїми знаками в обернені напрямки А8, В5 і т.д., що йдуть з інших пунктів А, В, ... на даний пункт, оскільки візування з цих точок виконується не на центр знака в точці С, а на його візирну ціль в точці S.

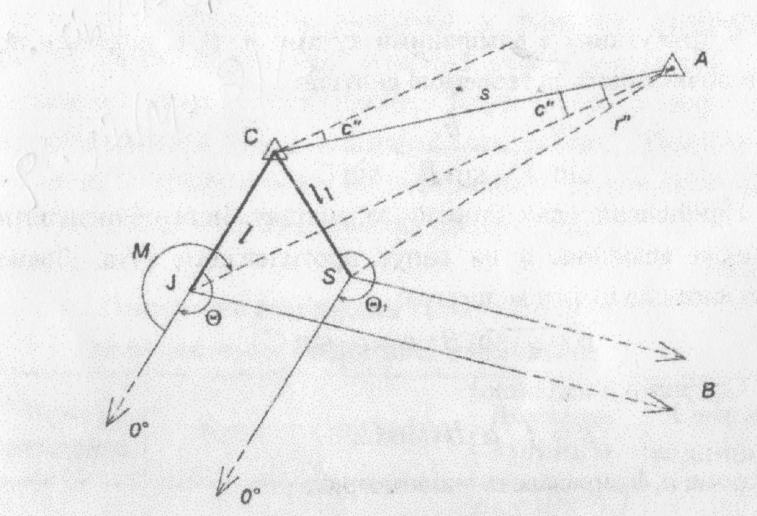
Схема до обчислення поправок за центрування та редукцію

Поправки за центрування теодоліта та редукцію візирної цілі обчислюють за формулами:

де l, θ, l_1,θ₁ - елементи центрування та редукції;

М - значення виміряних напрямків, для яких обчислюють поправки;

S - відстань між пунктами.

Лінійні елементи l та l₁ визначають на центрувальних листах до цілого міліметра, а кути θ i θ₁ з графічною точністю 15'.

Для контролю обчислення поправок с" і г" можна скористатись таблицями величин (а) = -20,6265 -sin(М + θ). Якщо лінійні елементи е та e₁ виразити в дециметрах, а відстані S - в кілометрах, то:

Поправки за центрування та редукцію в тріангуляції 1 - 2 класів обчислюються до 0,001", а в тріангуляції 3-4 класів до 0,01", після чого їх суму для кожного напрямку, приведеного до початкового, округлюють до 0,01" та 0,1" відповідно.