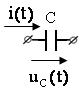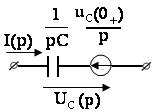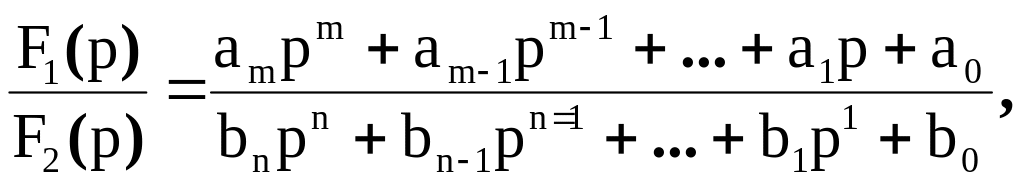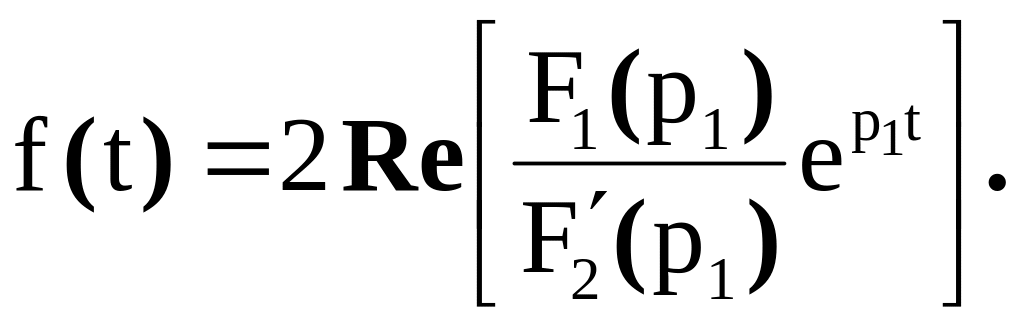4 Задание 3. Спектральный метод анализа электрических цепей

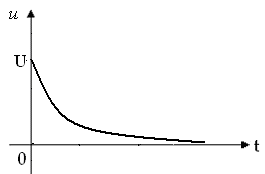
На вход цепи, полученной для задания 2, подается импульсное воздействие (рисунки 4.1,4.2), параметры и вид которого приведены в таблицах 4.1, 4.2.

4.1 Определить спектральную плотность входного напряжения ,построить его амплитудно-частотную (АЧХ) и фазо-частотную (ФЧХ) характеристики.

4.2 Определить комплексную передаточную функцию цепи , соответствующую искомой величине (таблица 4.3); построить ее амплитудно-частотную (АЧХ) и фазо-частотную (ФЧ Х) характеристики.

4.3 Определить спектральную плотность искомой величины.

4.4 По найденной спектральной плотности найти искомую величину, согласно заданному варианту (таблица 4.3)

Т а б л и ц а 4.1

Год поступления	Предпоследняя цифра зачетной книжки
Четный	0	1	2	3	4	5	6	7	8	9
Нечетный	9	8	7	6	5	4	3	2	1	0
	10	20	30	25	15	35	40	45	50	18
	800	300	400	600	500	800	700	600	700	900

Т а б л и ц а 4.2

Год поступления	Последняя цифра зачетной книжки
Четный	0	1	2	3	4	5	6	7	8	9
Нечетный	9	8	7	6	5	4	3	2	1	0
Вид импульса	4.1	4.2	4.1	4.2	4.1	4.2	4.1	4.2	4.1	4.2

Т а б л и ц а 4.3

Год поступления	Первая буква фамилии
Четный	АБВ	ГДЕ	ЖЗИ	КЛ	МН	ОПР	СТУ	ХФЦ	ЧШЩ	ЭЮЯ
Нечетный	ЭЮ Я	ЧШ Щ	ХФ Ц	СТ У	ОП Р	МН	КЛ	ЖЗ И	ГД Е	АБ В
Искомая величина			uR2	iR3	uR3	uR2		iR2	iR2	uR3

Рисунок 4.1

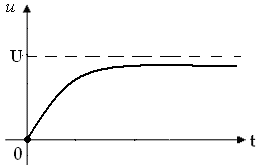
Рисунок 4.2

5. Методические указания к расчёту курсовой работы

5.1 Классический метод расчёта переходных процессов

Методика расчёта переходных процессов классическим методом включает следующие этапы:

а) Определение независимых начальных условий: ; независимые начальные условия определяются путём расчета установившегося режима в цепи до коммутации и с применением законов коммутации:

; ;

б) Запись дифференциальных уравнений по законам Кирхгофа для цепи после коммутации;

в) Запись выражения для искомого переходного тока или переходного напряжения в виде:

; ;

г) Определение принуждённого тока или принужденного напряжения путём расчёта установившегося режима в цепи после коммутации;

д) Определение свободного тока или напряжения .Для определения или составляется характеристическое уравнение и находятся его корни. Запись выражения или определяется типом корней характеристического уравнения.

ж) Определение постоянных интегрирования по начальным значениям искомой величины и её первой производной (для цепи второго порядка).

5.2 Операторный метод расчёта переходных процессов

Методика расчёта переходных процессов операторным методом включает следующие этапы:

а) Определение независимых начальных условий: .

б) Составление эквивалентной операторной схемы (схема составляется для цепи после коммутации).

Т а б л и ц а 5.1

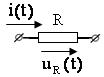
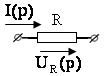
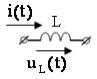
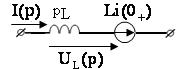
Эквивалентные операторные схемы пассивных элементов
Исходная схема	Операторная схема

в) Составление уравнений для определения изображения искомой величины, используя любой из методов расчёта: законы Кирхгофа в операторной форме, метод контурных токов, метод узловых потенциалов, метод эквивалентного генератора и т.п. (уравнения составляются для цепи после коммутации),

и определение изображения искомой величины.

г) Определение искомой величины (оригинала) по найденному изображению, используя теорему разложения.

Т а б л и ц а 5.2

Теорема разложения
Изображение имеет вид рациональной дроби: где m<n, - характеристическое уравнение. Оригинал определяется по теореме разложения.
Вид корней характеристического уравнения , для .	Теорема разложения
корни характеристического уравнения , − вещественные и различные	где
корни характеристического уравнения комплексные сопряженные
знаменатель имеет один нулевой корень: , корни характеристического уравнения , − вещественные и различные
знаменатель имеет один нулевой корень: , корни характеристического уравнения комплексные сопряженные

5.3 Расчет переходных процессов в линейных электрических цепях с помощью интеграла Дюамеля

Интеграл Дюамеля применяется для определения токов или напряжений в пассивной электрической цепи при подключении к источнику непрерывно из

меняющегося напряжения произвольной формы.

Методика расчёта переходных процессов в линейных электрических цепях с помощью интеграла Дюамеля включает следующие этапы:

а) Определение переходной функции цепи: переходной проводимости или переходной функции по напряжению . Переходная приводимость численно равна искомому току, а переходная функция по напряжению численно равна искомому напряжению при подключении цепи к постоянному напряжению U=1B при нулевых начальных условиях, Переходные функции цепи , определяются путём расчёта переходных процессов классическим или операторным методами при подключении цепи в момент t=0 к источнику единичного постоянного напряжения при нулевых начальных условиях.

б) Вычисление тока или напряжения с помощью интеграла Дюамеля:

Так как напряжение источника имеет различные аналитические выражения на разных интервалах времени, интервал интегрирования разбивается на отдельные участки и ток или напряжение, вычисляемые с помощью интеграла Дюамеля записываются для отдельных участков времени.

5.4. Спектральный метод анализа электрических цепей

Методика спектрального метода анализа электрических цепей включает этапы:

а) Определение спектральной плотности импульса входного напряжения с помощью прямого преобразования Фурье

б) Определение комплексной передаточной функцию цепи или .

в) Определение спектральной плотности реакции цепи или :

, .