13.Правило фаз Гиббса. Сведение многокомпонентных смесей к системе бинарных и тройных смесей.

При локальном термодинамическом равновесии компонентные соста­вы, а также плотности и вязкости фаз взаимосвязаны условием равен­ства химических потенциалов отдельных компонентов в сосуществующих фазах. Химический потенциал " "- го компонента в фазе   будет зависеть от всего состава фазы и фазового давления. Из-за этого, во­обще говоря, потенциалы должны зависеть, помимо состава фаз, также и от насыщенности в терминах капиллярного давления [18]. В пористой среде взаимодействия с твердыми поверхностями также могут влиять на величины химических потенциалов компонентов в фазах. Однако в первом приближении будем пренебрегать влиянием пористой среды на химические потенциалы.

Для закрытой равновесной термодинамической системы, а при локаль­ном термодинамическом равновесии в точке имеет место именно такая система, справедливо правило фаз Гиббса [18, 4]:

(2.1.5)

где - число степеней свободы /независимых переменных/ системы;

- число компонентов; - число фаз; - число внешних парамет­ров /обычно давление и температура/.

В случае двух компонентов и двух фаз = 2 и, следовательно, фазовые концентрации, плотности и вязкости фаз зависят только от давления и температуры системы. В случае трех компонентов и двух фаз = 3 и фазовые концентрации, плотности и вязкости уже зависят, помимо давления и температуры, от одной концентрации /или от их комбинации/, например,

Число степеней свободы открытой системы /такая рассматри­вается в задачах фильтрации/, равняется числу независимых переменных в уравнениях гидродинамики, а поскольку система уравнений должна быть замкнута, то и числу уравнений [4]:

( 2.1.6)

14.Численный метод решения задачи фильтрации многофазной многокомпонентной смеси. Строго неявный метод (SIP).

Система дифференциальных уравнений, описывающую многофазное изотермическое течение многокомпонентной смеси с учетом фазовых переходов компонентов из одной фазы в другую, сжимаемости породы и флюидов и действия гравитационных и капиллярных сил:

(2.1.3)

здесь - пористость в точке пласта, ,

- коэффициент, учитывающий упругоёмкость пласта,

- коэф­фициент пористости при атмосферном давлении .

Система (2.1.3) должна быть дополнена следующими замыкающими соотношениями:

(2.1.4)

В (2.1.4) - капиллярное давление между фазами   и  . При этом , где - безразмерная функция Леверетта, - контактный угол смачивания [92, 230]. Переменность компонентного состава фаз при фазовых переходах приводит к изменению межфазового натяжения . Последнее выражение (2.1.4), вообще говоря, соответствует условиям статического равновесия при насыщении порового пространства. Однако будем считать, что межфазовый обмен компонентов происходит при относительном движении фаз так же, как и в случае их покоя.

Итак, рассматривается течение двухфазной многокомпонентной уг­леводородной смеси в пласте, которое описывается системой уравнений (2.1.3, 2.1.4). При этом = 2 и = 2 и индекс "1" относится к газу, а индекс "2" к жидкости. С учетом безразмерных соотношений:

(2.2.1)

где характерные значения давления, проницаемости, плотности, вязкости, линейного размера, толщины и глубины за­легания пласта, соответственно, индекс " р " - означает размерную величину /остальные обозначения см. выше/. В двумерном случае из (2.1.3) с учетом переменной толщины пласта имеем:

(2.2.2)

где

- давление в газовой фазе; - капиллярное давление; - зависимость пористости от давления в области, занятой газом; зависимость пористости от давления в области, занятой жидкостью; - насыщенность жидкостью порового пространства;

;

.

При соответствующих граничных условиях решение системы (2.2.2) по­зволяет получить распределение давления и насыщенности в пласте про­извольной формы и толщины с произвольным размещением источников и стоков /скважин/ при учете сжимаемости флюидов и породы, гравитаци­онных и капиллярных сил.

Система (2.2.2) в силу ее нелинейности может быть решена только численными методами. В настоящей работе будем применять метод неполной разностной факторизации / SIP- метод/ [14, 29, 42] .

Разностные уравнения, аппроксимирующие систему (2.2.2) в матричном виде, выразим так:

(2.2.3)

Пусть далее

(2.2.3а)

и (2.2.3б)

где m - номер итерации.

Тогда из (2.2.3а) с учетом (2.2.3б) имеем следующее итерационное выражение:

(2.2.3в)

где (2.2.3г)

- матрица коэффициентов разностных уравнений;

- вспомогательная матрица, определяемая в [42] и позволяющая легко факторизовать систему (2.2.3в);

- искомая функция /вектор/;

- вектор, подобный вектору и выражающий правые части раз­ностных уравнений;

Модифицированная матрица должна по условию удовлет­ворять следующему соотношению

(а)

где и нижняя и верхняя треугольные матрицы, соответственно.

Тогда из (2.2.3в) и (а) следует

(б)

и далее, если , (в)

то из (б) следует (г)

Решение системы (2.2.3в) можно получить теперь следующим образом. Так как и - треугольные матрицы, то сначала из (г) опреде­ляется вектор

, (д)

а затем из (в) определяем вектор приращения искомых давле­ний на (m+1) итерации

(е)

Элемент матрицы в (2.2.3в) для некоторой точки (i, j) пространст­венной решетки имеет вид:

(2.2.4а)

+

В (2.2.4a) две последние строки выражают вспомогательную матрицу ,

и т.д. матрицы 2-го порядка,

, - диагональная матрица итерационных параметров, - матрицы 2-го порядка, определяемые ниже.

Выражение (2.2.4а) имеет место при решении разностных уравнений с последовательностью изменения индексов в следующем порядке: i=1,2,…M; j=1,2,…N

При порядке просчета с изменением индексов i= I,2,..,M; j= N, N-1,… 2,1 вспомогательная матрица в (2.2.4а) должна быть представлена так:

(2.2.4б)

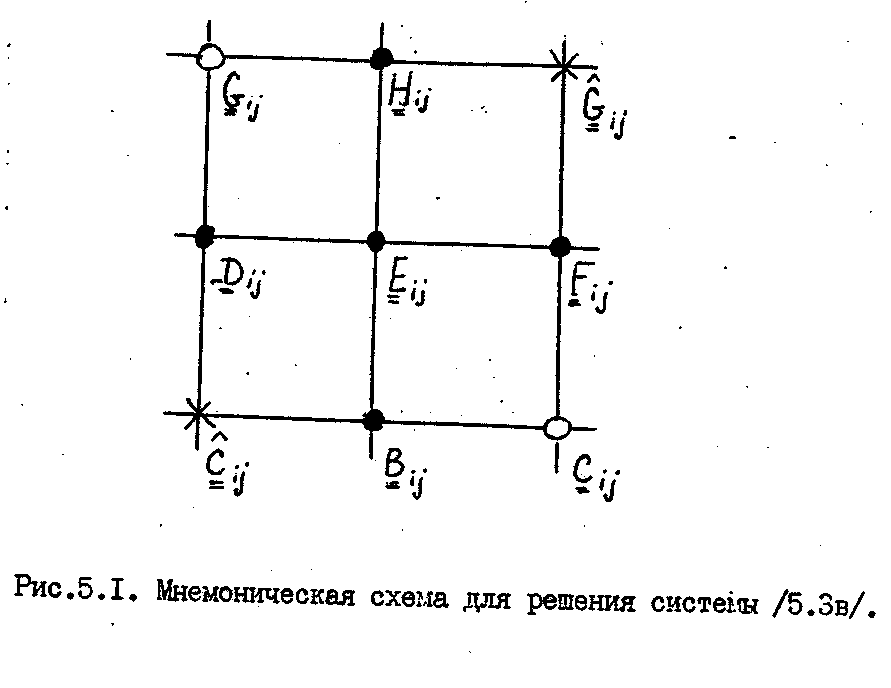
Мнемоническая схема для решения системы /2.2.3в/ при возрастании индексов имеет вид, представленный на рис.2.1 /черные и светлые кружочки/, при изменении индекса j- в обратном порядке /черные кружочки и крестики/.

Следуя работе [273] , имеем при возрастании индексов следующие рекуррентные выражения для коэффициентов прогонки:

(2.2.5)

Вектор при этом определяется /прямая прогонка/ по формуле/2.2.6а/

(2.2.6а)

(i=1,2,..., М; j= 1,2, …, N )

Значения получаются /обратная прогонка/ по рекуррентной формуле

(2.2.6б)

При расчете с изменением индексов следующим образом: i = I,2...M; j= N, N-1 , ...2,1 выражения для коэффициентов имеют вид:

(2.2.7)

Вектор в этом случае определяется по формуле

(2.2.8а)

(I =1,2, М; j= N, N-1, 2,1)

Значения получаются по формуле

(2.2.8б)

Пусть далее выражение в квадратных скобках при вычислении в (2.2.5) и (2.2.7) имеет вид

,

тогда (2.2.9)

Отсюда следует, что элементы матриц и , которые

являются строго нижней и верхней треугольными матрицами, равны

(2.2.10а)

и (2.2.10б)

Для улучшения сходимости итерационного процесса при решении разностных уравнений рекомендуется менять порядок расчета от итера­ции к итерации, а именно, нечетная итерация имеет порядок просчета с изменением индексов i= 1,2,... М; j= 1,2,... N, четная итерация- i=1,2, ... М; j = N, N-1,...2, 1 [45]. Затем поря­док просчета, повторяется.

Элементы матриц и т.д. в /2.2.4а/ имеют вид:

(2.2.11)

Правая часть уравнения (2.2.3) для некоторой точки (i, j) разност­ной сетки - вектор вида

и далее,

(2.2.12)

( k=1, 2)

Выражение для некоторой точки (i, j) вектор вида

(2.2.13)

В (2.2.11), (2.2.12), (2.2.13) - давление на предыдущем времен­ном слое, - шаги по пространственной и временной разностным сеткам.

Для улучшения сходимости итерационного процесса применяется матрица итерационных параметров

При этом величины могут быть получены следующим образом [42]. Из анализа устойчивости разностных уравнений, полученных при рассмотрении линеаризованных дифференциальных уравнений, следу­ет

где - число точек по оси X, - число точек по оси Y,

Далее принимаем, что итерационный параметр для лучшей сходимо­сти итерационного процесса изменяется от итерации к итерации [42, 45]

(2.2.14)

Затем цикл изменения , повторяется. Таким образом, итерационный параметр изменяется от до 0 согласно (2.2.14). Следует отметить, что последовательность итерационных параметров может быть как убывающей, так и возрастающей.

Для улучшения сходимости итерационного процесса можно применить еще и итерационный параметр в формуле (2.2.3г) [42] , т.е.

(2.2.3^’г)

/При этом в первом приближении можно брать значения /.

15.Основные уравнения в двумерной постановке для задач фильтрации многокомпонентной смеси.

Система дифференциальных уравнений, описывающую многофазное изотермическое течение многокомпонентной смеси с учетом фазовых переходов компонентов из одной фазы в другую, сжимаемости породы и флюидов и действия гравитационных и капиллярных сил:

(2.1.3)

здесь - пористость в точке пласта, ,

- коэффициент, учитывающий упругоёмкость пласта,

- коэф­фициент пористости при атмосферном давлении .

Система (2.1.3) должна быть дополнена следующими замыкающими соотношениями:

(2.1.4)

В (2.1.4) - капиллярное давление между фазами   и  . При этом , где - безразмерная функция Леверетта, - контактный угол смачивания [92, 230]. Переменность компонентного состава фаз при фазовых переходах приводит к изменению межфазового натяжения . Последнее выражение (2.1.4), вообще говоря, соответствует условиям статического равновесия при насыщении порового пространства. Однако будем считать, что межфазовый обмен компонентов происходит при относительном движении фаз так же, как и в случае их покоя.

Итак, рассматривается течение двухфазной многокомпонентной уг­леводородной смеси в пласте, которое описывается системой уравнений (2.1.3, 2.1.4). При этом = 2 и = 2 и индекс "1" относится к газу, а индекс "2" к жидкости. С учетом безразмерных соотношений:

(2.2.1)

где характерные значения давления, проницаемости, плотности, вязкости, линейного размера, толщины и глубины за­легания пласта, соответственно, индекс " р " - означает размерную величину /остальные обозначения см. выше/. В двумерном случае из (2.1.3) с учетом переменной толщины пласта имеем:

(2.2.2)

где

- давление в газовой фазе; - капиллярное давление; - зависимость пористости от давления в области, занятой газом; зависимость пористости от давления в области, занятой жидкостью; - насыщенность жидкостью порового пространства;

;

.

При соответствующих граничных условиях решение системы (2.2.2) по­зволяет получить распределение давления и насыщенности в пласте про­извольной формы и толщины с произвольным размещением источников и стоков /скважин/ при учете сжимаемости флюидов и породы, гравитаци­онных и капиллярных сил.

Система (2.2.2) в силу ее нелинейности может быть решена только численными методами.