1.Представление дифференциальных уравнений параболического типа в разностной форме

Известно, что любую функцию , непрерывную и имеющую все необходимые производные при x=a, можно представить в виде ряда Тейлора:

(1.1.1)

Отсюда видно, что по известным значениям функции и её производных можно определять значения функции в близлежайшей точке.

Пусть на оси OX имеется отрезок MN, разбитый на n равных частей. Тогда расстояние (шаг) между соседними точками

0 1 i-1 i i+1…..n-1 n

O M N Х

Выберем произвольные точки на линии MN: (i-1), i, (i+1) и при помощи (1.1.1) запишем значения функции в точках (i-1) и (i+1) через значения функции и её производных в точке i. Для точки (i-1): (x-a) = - h, а для точки (i+1): (x-a) = h.

	(1.1.2)
	(1.1.3)

Здесь - значение производных в точке i.

Первая производная из уравнений (1.1.2) и (1.1.3) будет выражаться так:

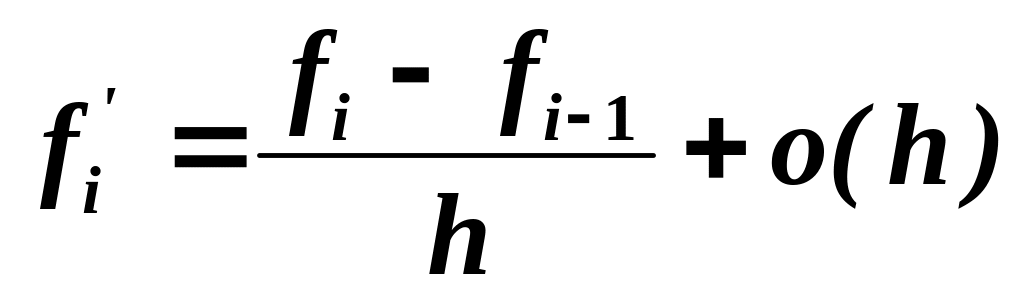
	(1.1.5)

– сумма соответствующих остаточных членов ряда (1.1.2) или (1.1.3), поделённых на h .

Можно получить более точное выражение для первой производной по x в точке i, если вычесть (1.1.3) из (1.1.2)

			(1.1.6)
	Разобьём интервал времени [O,T] на k- равных интервалов, тогда шаг по времени .	(1.1.8)

Где j – соответствует временному слою , а j+1 временному слою (j+1)Δt

Можно получить боле точное выражение первой производной по времени через конечные разности.

Запишем значение функции и через её значения в точке j+1 с использованием (1.1.1).

		(а)
		(б)
У множив (а) на 4 и вычитая из (б), получим для

Т.е. с точностью до , если отбросим остаточные члены о ( ) в выражении (1.1.9).

Рассмотрим представление в конечно – разностной форме одномерного дифференциального уравнения параболического типа

; ,

(1.2.1)

которое описывает фильтрацию сжимаемой жидкости (аналогично уравнению теплопроводности)

Используя уравнения (1.1.5) и (1.1.7) предыдущего раздела имеем выражение

(1.2.2)

Здесь - погрешность аппроксимации исходного дифференциального уравнения (1.2.1) конечно – разностным уравнением. Принимается, что

В уравнении (1.2.2) левую часть можно рассматривать на различных временных уровнях: либо на слое jt и тогда имеем уравнение

(1.2.3)

либо на временном слое (j+1) t и тогда уравнение (1.2.2) имеет вид

(1.2.4)

При записи этих уравнений пренебрегается величиной

В уравнении (1.2.3) имеется лишь одна неизвестная величина (Считается, что все величины на временном слое известны). Такое уравнение называется явным сеточным уравнением.

Уравнение (1.2.4), где имеются три неизвестные величины , , называется неявным.

Применяя последовательно уравнение (1.2.3) к каждой точке i сеточной области (с учетом граничных условий), можно получить искомое решение на временном слое и т.д. Таким образом, оно позволяет явным образом находить решение задачи в каждый момент времени .

Записывая неявное уравнение (1.2.4) для точек , получаем систему из (n-1) уравнения с (n+1) неизвестным. Граничные условия в точках i=0 и i=n дают еще два условия. Следовательно, чтобы решить задачу на временном слое , требуется решить систему (n+1) уравнения с (n+1) неизвестным.

Таким образом, использование численных методов сводит интегрирование дифференциального уравнения в частных производных (1.2.1) и соответствующих краевых условий к чисто алгебраической задаче.