Розділ 4 Статистичні методи виявлення наявності кореляційних звязків

У багатовимірних динамічних рядах кореляційні звязки слід вивчати в такій послідовності:

4.1 Встановити за допомогою кореляційного поля характер звязку між факторною і результативними ознаками

4.2 Перевірити наявність автокореляції у багатовимірних динамічних рядах

4.3 У разі її виявлення усунути автокореляцію. Побудувати регресійну модель

4.4 Дати економічну інтерпретацію цієї моделі.

Алгоритм розрахунку факторної та результативної ознак для проведення кореляційно-регресійного аналізу наведено в таблиці Д1.

Для попереднього виявлення наявності звязку між факторною і результативними ознаками, а також для вибору форми звязку застосовують графічний метод.

Автокореляція – це залежність наступних рівнів динамічного ряду від попередніх. Наявність автокореляції порушує одну з передумов регресійного аналізу – незалежність спостережень і приводить до викривлення його результатів.

З метою виявлення присутності чи відсутності автокореляції визначаємо значення коефіцієнтів автокореляції в рядах х та у та порівняємо їх з критичними значеннями.

Коефіцієнт автокореляції обчислюємо за формулою:

для ряду х:

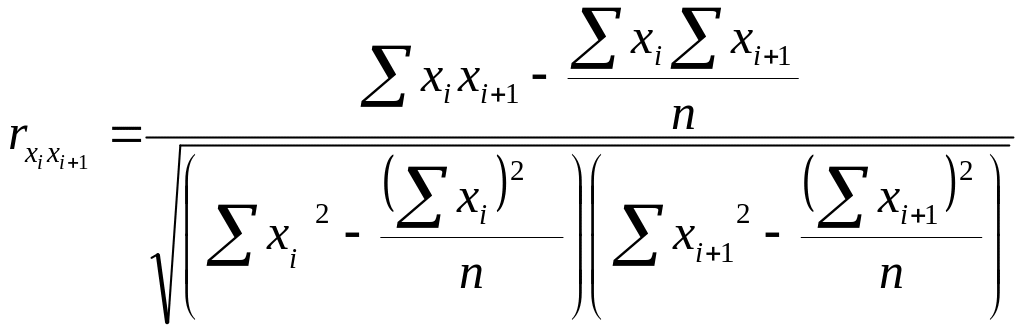
Для ряду у:

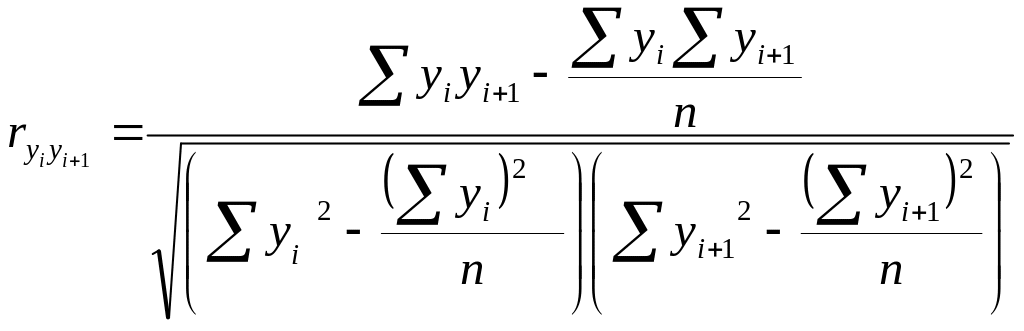
Існує декілька методів усунення автокореляції. Одним з таких методів є метод введення змінної величини в рівняння регресії, де вона виконує роль фактора часу. В цьому випадку рівняння регресії матиме вигляд:

,

де - параметр, який характеризує середній приріст результативної ознаки на одиницю приросту факторної ознаки ;

- середній щорічний приріст під впливом зміни комплексу факторів, крім .

Для визначення цих параметрів складають систему нормальних рівнянь, яку розв’язують методом підстановок або Крамера.

Розв’язок системи спрощується, якщо відлік часу беруть з середини динамічного ряду, тоді .

Якщо в такий спосіб автокореляцію усунуто, то залишкові величини повинні бути між собою незалежними:

Цю гіпотезу перевіряють за допомогою коефіцієнта автокореляції залишкових величин, який обчислюють з певним часовим зсувом (лагом). При р=1 коефіцієнт автокореляції обчислюють за формулою:

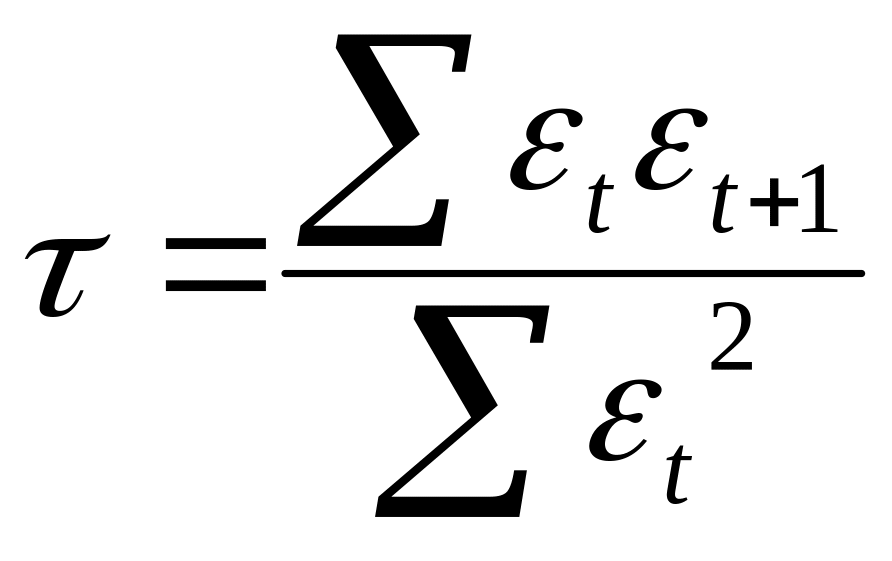
Коефіцієнт приймає значення в межах від -1 до1.

Фактичне значення коефіцієнта автокореляції порівнюємо з критичним, яке беруть в таблицях математичної статистики. Якщо критичне значення автокореляції більше за фактичне, то це дає підстави стверджувати , що автокореляція залишкових величин неістотна. Отже автокореляція в рядах х, цим способом усунуто і побудовану кореляційну модель можна вважати адекватною.

Дослідимо кореляційну залежність між зростанням коефіцієнта оборотності виробничих запасів і рентабельність продукції.

Коефіцієнт оборотності виробничих запасів = ;

Рентабельність продукції =

Дані про показники наведені в таблиці 4.2

Таблиця 4.2

Роки	Доход	Середня вартість виробничих запасів	Валовий прибуток	Собівартість продукції	Коефіцієнт оборотності виробничих запасів	Рентабель-ність продукції
2002	1710,7	144,85	273	1437,7	11,81	19
2003	2112,8	73,85	253,2	1859,6	28,6	13,6
2004	3179,9	78,25	453,6	2725,63	40,6	16,6

Факторною ознакою буде коефіцієнт оборотності виробничих запасів, результативною – рентабельність продукції.

П обудуємо кореляційне поле .

Рисунок 4.1 - Кореляційне поле.

Описуємо зв'язок лінійним рівнянням регресії.

Усуваємо автокореляцію шляхом введення додаткової змінної t в рівняння регресії, яке в цьому випадку буде мати вигляд:

Y = a₀ +a₁x +a₂t

П

a₀n +a₁Σx+ a₂Σt =Σy

a₀ Σx + a₁Σx² + a₂Σxt= Σxy

a₀ Σt + a₁Σxt + a₂Σt²= Σty

араметри даної функції визначаємо за методом найменших квадратів з системи нормальних рівнянь

Всі необхідні розрахунки проводимо в таблиці 4.3

Таблиця 4.3

t	у	х	t2	x2	уt	хt	xy
-1	19	11,81	1	139,5	-19	-11,81	224,39
0	13,6	28,6	0	817,9	0	0	388,9
1	16,6	40,6	1	1648,4	16,6	40,6	673,96
Σ 3a0 +81a1+0 = 49,2 81а +2605,8a1 +28,8a2=1287,35 0+28,8 a1 +2a2 = -2,4 t=0	49,2	81	2	2605,8	-2,4	28,79	1287,35

Систему рівнянь можна розв’язати за методом Крамера або методом підстановок.

Розв’язання системи рівнянь методом Крамера:

Δ= =

Δ₀= =

Δ₁= =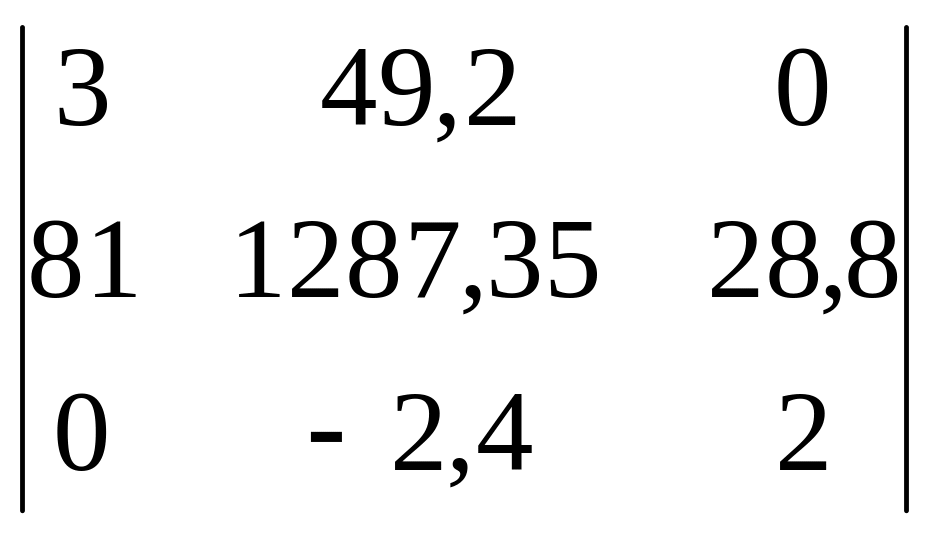

Δ₂= =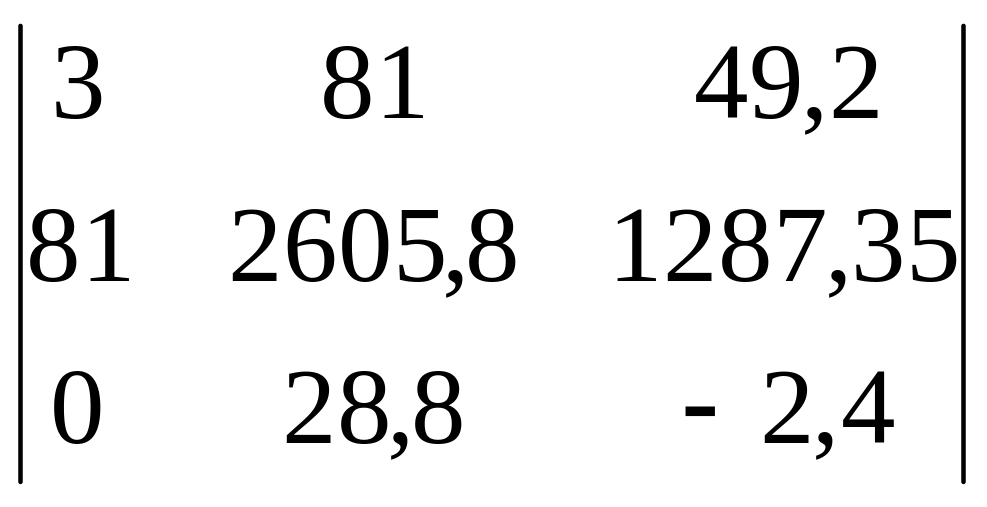

a₀ = ;

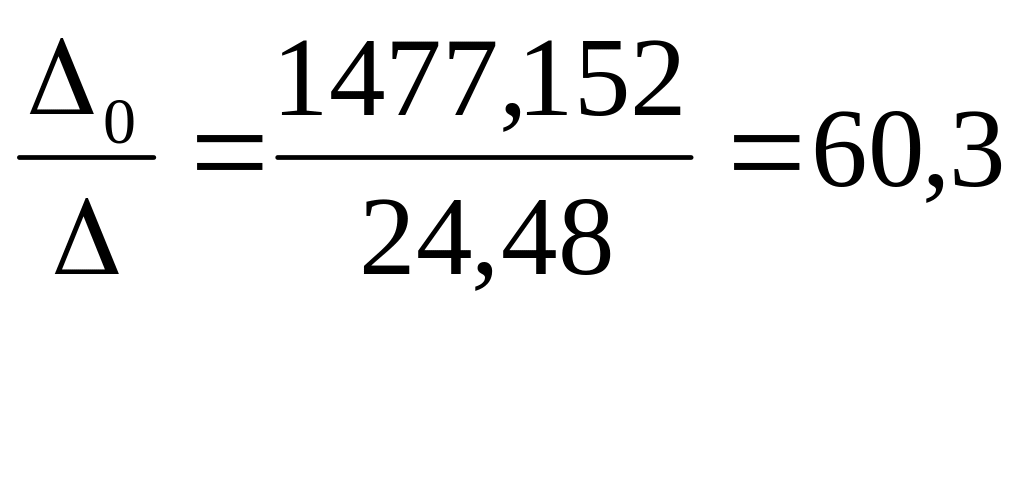a₁=

a₂ =

Розв’язання системи рівнянь методом підстановок.

; ;

Тоді отримаємо вираз:

, тоді ,

Рівняння регресії матиме вигляд:

Визначаємо теоретичні рівні:

Перевіряємо чи залишкові величини є незалежними. Розрахунки приведенні в таблиці 4.4.

Таблиця 4.4 - Розрахунок коефіцієнта автокореляції

	у	х	Y(t)	εt	εt+1	εt εt+1	εt2
-1	19	11,81	18,8	0,2	-0,08	-0,016	0,04
0	13,6	28,6	13,68	-0,08	0,28	-0,022	0,064
1	16,6	40,6	16,32	0,28	0,2	0,056	0,078

Коефіцієнт автокореляції

r=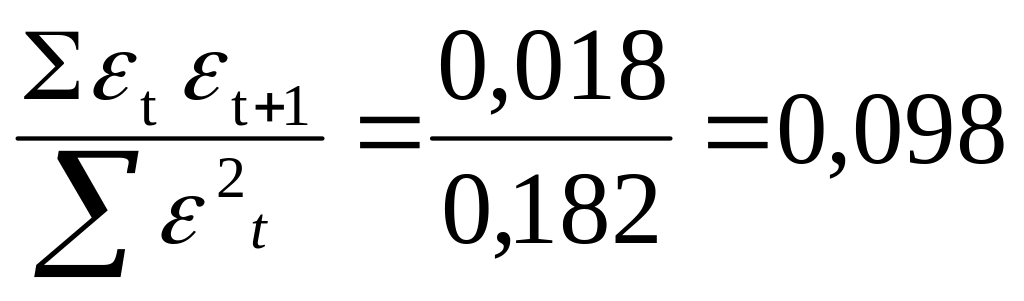

Отже при дослідженні кореляційної залежності між коефіцієнтом оборотності виробничих запасів та рентабельністю продукції виявлено прямий кореляційний зв'язок. Для усунення автокореляції було введено змінну t. Так, як =0,098 є меншим за табличне значення 0,253 це значить, що автокореляція усунено.