28. Шейкерная сортировка

1. Сортировка перемешиванием (Шейкерная сортировка) (англ. Cocktail sort) — разновидность пузырьковой сортировки. Анализируя метод пузырьковой сортировки можно отметить два обстоятельства. Во-первых, если при движении по части массива перестановки не происходят, то эта часть массива уже отсортирована и, следовательно, ее можно исключить из рассмотрения. Во-вторых, при движении от конца массива к началу минимальный элемент “всплывает” на первую позицию, а максимальный элемент сдвигается только на одну позицию вправо.

2. Эти две идеи приводят к следующим модификациям в методе пузырьковой сортировки. Границы рабочей части массива (т.е. части массива, где происходит движение) устанавливаются в месте последнего обмена на каждой итерации. Массив просматривается поочередно справа налево и слева направо.

3. Лучший случай для этой сортировки — отсортированный массив (О(n)), худший — отсортированный в обратном порядке (O(n²)).

4. Наименьшее число сравнений в алгоритме Шейкер-сортировки C=N-1. Это соответствует единственному проходу по упорядоченному массиву (лучший случай)

5. Код программы на языке программирования С++

6. #include <vcl.h>

7. #include <conio.h>

8. #include <iostream.h>

9. #pragma hdrstop

10. #pragma argsused

12. // Шейкер-сортировка

14. int main(int argc, TCHAR* argv[])

15. {

16. const int Count = 10;

17. int TestArr[Count] = {3, 1, 5, 8, 1, 0, 6, 4, 6, 7};

19. ShakerSort(TestArr,0,Count);

20. ArrayOutput(TestArr,0,Count);

22. return 0;

23. }

25. //Поменять местами 2 элемента

26. void Swap(int* e1, int* e2)

27. {

28. *e1 ^= *e2;

29. *e2 ^= *e1;

30. *e1 ^= *e2;

31. }

33. void ShakerSort(int Arr[], int Start, int N)

34. {

35. int Left, Right; //границы сортировки

37. Left = Start;

38. Right = N - 1;

41. do

42. {

43. //Сдвигаем к началу массива "легкие элементы"

44. for (int i = Right; i > Left; i--)

45. {

46. if (Arr[i] < Arr[i - 1])

47. {

48. Swap(&Arr[i], &Arr[i-1]);

49. }

50. }

52. Left = Left + 1;

54. //Сдвигаем к концу массива "тяжелые элементы"

55. for (int i = Left; i < Right; i++)

56. {

57. if (Arr[i] > Arr[i + 1])

58. {

59. Swap(&Arr[i], &Arr[i + 1]);

60. }

61. }

63. Right = Right - 1;

64. }

65. while (Left <= Right);

66. }

68. //Вывод элементов массива на консоль

69. void ArrayOutput(int* Arr, int Start, int N)

70. {

71. for (int i = Start; i < N; i++)

72. {

73. cout << Arr[i] << '\n';

74. }

75. getch();

76. }

29. Метод сортировки Шелла.

1. Сортировка Шелла является довольно интересной модификацией алгоритма сортировки простыми вставками.

2. Рассмотрим следующий алгоритм сортировки массива a[0].. a[15].

3. 

4. 1. Вначале сортируем простыми вставками каждые 8 групп из 2-х элементов (a[0], a[8[), (a[1], a[9]), ... , (a[7], a[15]).

5. 

6. 2. Потом сортируем каждую из четырех групп по 4 элемента (a[0], a[4], a[8], a[12]), ..., (a[3], a[7], a[11], a[15]).

7. 

8. В нулевой группе будут элементы 4, 12, 13, 18, в первой - 3, 5, 8, 9 и т.п.

9. 3. Далее сортируем 2 группы по 8 элементов, начиная с (a[0], a[2], a[4], a[6], a[8], a[10], a[12], a[14]).

10. 

11. 4. В конце сортируем вставками все 16 элементов.

12. 

13. Очевидно, лишь последняя сортировка необходима, чтобы расположить все элементы по своим местам. Так зачем нужны остальные ?

14. Hа самом деле они продвигают элементы максимально близко к соответствующим позициям, так что в последней стадии число перемещений будет весьма невелико. Последовательность и так почти отсортирована. Ускорение подтверждено многочисленными исследованиями и на практике оказывается довольно существенным.

15. Единственной характеристикой сортировки Шелла является приращение - расстояние между сортируемыми элементами, в зависимости от прохода. В конце приращение всегда равно единице - метод завершается обычной сортировкой вставками, но именно последовательность приращений определяет рост эффективности.

16. Использованный в примере набор ..., 8, 4, 2, 1 - неплохой выбор, особенно, когда количество элементов - степень двойки. Однако гораздо лучший вариант предложил Р.Седжвик. Его последовательность имеет вид

17. 

18. При использовании таких приращений среднее количество операций: O(n^7/6), в худшем случае - порядка O(n^4/3).

19. Обратим внимание на то, что последовательность вычисляется в порядке, противоположном используемому: inc[0] = 1, inc[1] = 5, ... Формула дает сначала меньшие числа, затем все большие и большие, в то время как расстояние между сортируемыми элементами, наоборот, должно уменьшаться. Поэтому массив приращений inc вычисляется перед запуском собственно сортировки до максимального расстояния между элементами, которое будет первым шагом в сортировке Шелла. Потом его значения используются в обратном порядке. При использовании формулы Седжвика следует остановиться на значении inc[s-1], если 3*inc[s] > size.

20. int increment(long inc[], long size) {

21. int p1, p2, p3, s;

23. p1 = p2 = p3 = 1;

24. s = -1;

25. do {

26. if (++s % 2) {

27. inc[s] = 8*p1 - 6*p2 + 1;

28. } else {

29. inc[s] = 9*p1 - 9*p3 + 1;

30. p2 *= 2;

31. p3 *= 2;

32. }

33. p1 *= 2;

34. } while(3*inc[s] < size);

36. return s > 0 ? --s : 0;

37. }

39. template<class T>

40. void shellSort(T a[], long size) {

41. long inc, i, j, seq[40];

42. int s;

44. // вычисление последовательности приращений

45. s = increment(seq, size);

46. while (s >= 0) {

47. // сортировка вставками с инкрементами inc[]

48. inc = seq[s--];

50. for (i = inc; i < size; i++) {

51. T temp = a[i];

52. for (j = i-inc; (j >= 0) && (a[j] > temp); j -= inc)

53. a[j+inc] = a[j];

54. a[j+inc] = temp;

55. }

56. }

57. }

59. Часто вместо вычисления последовательности во время каждого запуска процедуры, ее значения рассчитывают заранее и записывают в таблицу, которой пользуются, выбирая начальное приращение по тому же правилу: начинаем с inc[s-1], если 3*inc[s] > size.

30.Метод быстрой сортировки Хоара

Сортировка Хоара это третий, и думаю последний, метод относящийся к обменным сортировкам. Этот метод метод признан одним из лучших методов сортировки, которые когда-либо придумали. Он даже носит название "Быстрой сортировки".

В методе Хоара первоначально выделяют базовый элемент, относительно которого ключи с большим весом перебрасываются вправо, а с меньшим влево. Базовый элемент сравнивается с противоположным элементом.

В качестве базового элемента очень удобно брать крайние элементы.

Давайте рассмотрим пример:

Дано множество

{9,6,3,4,10,8,2,7}

Берем 9 в качестве базового элемента. Сравниваем 9 с противоположностоящим элементом, в данном случае это 7. 7 меньше, чем 9, следовательно элементы меняются местами.

{7,6,3,4,10,8,2,9}

Далее начинаем последовательно сравнивать элементы с 9, и менять их местами в зависимости от сравнения.

{7,6,3,4,10,8,2,9}

{7,6,3,4,10,8,2,9}

{7,6,3,4,10,8,2,9}

{7,6,3,4,9,8,2,10} - 9 и 10 меняем местами.

{7,6,3,4,8,9,2,10} - 9 и 8 меняем местами.

{7,6,3,4,8,2,9,10} - 2 и 9 меняем местами.

После такого перебрасывания элементов весь массив разбивается на два подмножетсва, разделенных элементом 9.

{7,6,3,4,8,2}

{10}

Далее по уже отработанному алгоритму сортируются эти подмножества. Подмножество из одного элемента естественно можно не сортировать. Выбираем в первом подмножестве базовый элемент 7.

{7,6,3,4,8,2}

{2,6,3,4,8,7} - меняем местами 2 и 7.

{2,6,3,4,8,7}

{2,6,3,4,8,7}

{2,6,3,4,8,7}

{2,6,3,4,7,8}- меняем местами 7 и 8

Получили снова два подмножества.

{2,6,3,4}

{8}

А дальше все происходит аналогично... В результате можно родить такую программу %) :

int QuickSort(int *array, int left, int right)

{

long base, opposite, p;

int c;

base=left;

opposite=right;

while (base!=opposite){

if ((array[base]>array[opposite])^(base>opposite)){

c=array[base];

array[base]=array[opposite];

array[opposite]=c;

p=base;

base=opposite;

if (p<opposite)

opposite=p+1; else opposite=p-1;

} else {

if (base<opposite)

opposite--; else opposite++;

};

};

if (left<base-1) QuickSort(array,left,base-1);

if (base+1<right) QuickSort(array,base+1,right);

};

31.Метод турнирной сортировки

32. Метод пирамидальной сортировки

Пошаговое описание алгоритма 1. Построение пирамиды Пирамида представляет собой дерево, в котором каждый узел имеет не более двух потомков, причем узел всегда больше или равен своим потомкам (таким образом, на вершине дерева всегда находится наибольший элемент). Если в исходном массиве n элементов, то последние (n / 2) элемента становятся основанием пирамиды (эти элементы являются листьями дерева, т.е. у них нет потомков, поэтому для них вышеуказанное правило выполняется автоматически). Удобнее всего поместить пирамиду в массив. При этом распределение индексов массива по узлам дерева будет выглядеть так (на этом рисунке все цифры - это индексы элементов массива, а ни в коем случае не значения этих элементов): 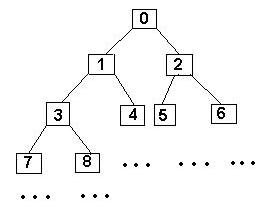Таким образом, для того, чтобы каждый узел дерева был больше своих потомков, каждый элемент массива a[i] должен быть больше или равен элементам a[2 * i + 1] и a[2 * i + 2]. 2. Сортировка В этой части алгоритма мы перемещаем в конец массива максимальный элемент, затем исключаем его из дальнейшего процесса сортировки. Поскольку максимальный элемент всегда находится на вершине пирамиды, мы должны поменять местами элементы a[0] и a[n-1] (т.е. последний элемент). Причем элемент a[n-1] необходимо добавлять так, чтобы не нарушился порядок пирамиды (при этом пирамиду придется частично перестроить). Далее мы будем рассматривать массив только до (n-2)-го элемента. На следующем шаге мы меняем местами a[0] и a[n-2] и далее рассматриваем массив только до (n-3)-го элемента. Повторяем всю эту процедуру до тех пор, пока в рассматриваемой части массива не останется один элемент. Реализация на C# Класс PyramidSorting, содержащий функцию пирамидальной сортировки, и класс Test для тестирования этой функции:

class PyramidSorting { //add 1 element to the pyramid static int add2pyramid(double[] arr, int i, int N) { int imax; double buf; if((2*i+2) < N) { if(arr[2*i+1] < arr[2*i+2]) imax = 2 * i + 2; else imax = 2 * i + 1; } else imax = 2 * i + 1; if(imax >= N) return i; if(arr[i] < arr[imax]) { buf = arr[i]; arr[i] = arr[imax]; arr[imax] = buf; if(imax < N/2)i = imax; } return i; } public static void sorting(double[] arr, int len) { //step 1: building the pyramid for(int i = len/2 - 1; i >= 0; --i) { long prev_i = i; i = add2pyramid(arr, i, len); if(prev_i != i) ++i; } //step 2: sorting double buf; for(int k = len-1; k > 0; --k) { buf = arr[0]; arr[0] = arr[k]; arr[k] = buf; int i = 0, prev_i = -1; while(i != prev_i) { prev_i = i; i = add2pyramid(arr, i, k); } } } }

class Test { static void Main(string[] args) { double[] arr = new double[100]; //fill the array with random numbers Random rd = new Random(); for(int i = 0; i < arr.Length; ++i) { arr[i] = rd.Next(1, 101); } System.Console.WriteLine("The array before sorting:"); foreach(double x in arr) { System.Console.Write(x + " "); } PyramidSorting.sorting(arr, arr.Length); System.Console.WriteLine("\n\nThe array after sorting:"); foreach(double x in arr) { System.Console.Write(x + " "); } System.Console.WriteLine("\n\nPress the <Enter> key"); System.Console.ReadLine(); } }

Функция add2pyramid() добавляет один элемент к пирамиде, перестраивая ее таким образом, чтобы не нарушалось правило, согласно которому узел не может быть меньше своих потомков. Функция sorting() отвечает непосредственно за сортировку.