Вопросы по курсу Статистика.

№1.Понятие статистики. История статистики.

Статистика одна из древнейших отраслей знаний, возникшая на базе хозяйственного учета. Ее возникновение связано с потребностями общества в различного рода сведениях.

Полагают, что термин статистика произошел от латинских слов stato (государство) и status (положение, состояние).

Под статистикой в широком смысле понимается наука, которая изучает с количественной стороны массовые явления и их закономерности.

Общая теория статистики – методологическая наука, наука о методе, который применим для выявления закономерностей в любой области, где выводы строятся на основе массового наблюдения, где имеет место вариация признака у единичных элементов совокупности, где общие закономерности могут проявляться только через взаимопогашение случайностей у отдельных единиц.

В средние века оно означало политическое состояние государства. Первоначально употреблялся в значении слова «государствоведение». Впервые в науку этот термин был введен в 1749 г. немецким ученым Готфридом Ахенвалем, выпустившим книгу о государствоведении. 

Статистика как наука стала развиваться с середины XVII в. по двум направлениям: описательному и математическому, т.е. у истоков статистической науки стояли две школы — немецкая описательная и английская школа политических арифметикой.

Представители описательной школы стремились систематизировать существующие способы описаний государств, создать теорию такого рода описаний, разработать их подробную схему, вести описание только в словесной форме, без цифр и вне динамики, т. е. без отражения особенностей развития государств в те или иные периоды, а только лишь на момент наблюдении. Видными представителями описательной школы были Г.Конринг (1606—1661), Г.Ахенваль (1719—1772), А.Бюшинг (1724-1793) и др.

Политические арифметики ставили целью изучать общественные явления с помощью числовых характеристик (меры веса и числа). Политические арифметики видели основное назначение статистики в изучении массовых общественных явлений, осознавали необходимость учета в статистическом исследовании требований закона больших чисел, поскольку закономерность может проявиться лишь при достаточно большом объеме анализируемой совокупности. Школа политических арифметиков имела два направления: демографическое — Дж.Граунт (1620—1674), Э.Галлей (1656—1742) — и статистико-экономическое — глава школы У.Петти (1623—1687). Как показала история, что именно школа политических арифметиков явилась истоком возникновения современной статистики как науки. 

В первой половине XIX в. возникло третье направление статистической науки – статистико-математическое. Среди представителей этого направления следует отметить бельгийского статистика Адольфа Кетле (1796—1874 гг.) – основоположника учения о средних величинах. Математическое направление в статистике развивалось в работах Ф.Гальтона (1822-1911 гг.) и К.Пирсона (1857-1936 гг.); В.Госсета (1876-1937 гг.), более известного под псевдонимом Стьюдент; Р.Фишера (1890-1962 гг.); М.Митчела (1874-1948 гг.) и др. Представители этого направления считали основой статистики теорию вероятностей, составляющую одну из отраслей прикладной математики. 

С развитием статистической науки, расширением сферы практической статистической работы изменялось и содержание понятия «статистика». В настоящее время данный термин употребляется в трех значениях:

 - отрасль практической деятельности людей, направленную на сбор,  обработку и анализ данных, характеризующих социально-экономическое развитие страны, ее регионов, отраслей экономики, отдельных предприятий;

-  наука, занимающаяся разработкой теоретических положений и методов, используемых статистической практикой. Между статистической наукой и статистической практикой существует тесная связь. Статистическая практика применяет правила, выработанные наукой. В свою очередь статистическая наука опирается на материалы практики и, обобщая опыт практики, разрабатывай новые положения;

-  статистикой часто называют статистические данные, представленные в отчетности предприятий, организаций, а также публикуемые в сборниках, справочниках, периодической прессе, которые представляют собой результат статистической работы.

№2.Предмет статистика.

В современном обществе важную роль в механизме управления экономикой играет статистика. Она осуществляет сбор, научную обработку, обобщение и анализ информации, характеризующей развитие экономики страны, уровня жизни населения и других общественных явлений и процессов.

Статистика — это ряды цифр, которые характеризуют различные стороны жизни государства.

Статистика — это род практической деятельности людей цель которой сбор, обработка и анализ информации.

Статистика — это наука, разрабатывающая статистическую методологию т.е. набор приемов и способов сбора, обработки и анализа информации.

Таким образом, статистика — это общетеоретическая наука (комплекс научных дисциплин), которая изучает количественную сторону качественно определенных массовых социально-экономических явлений и процессов, иэ состав, распределение, размещение в пространстве, движение во времени выявляя действующие взаимозависимости и закономерности в конкретных условиях места и времени.

Объектом изучения статистики является общество, протекающие в нём процессы и закономерности развития.

Статистика как наука представляет собой целостную систему научных дисциплин:

Общая теория статистики — разрабатывает теорию статистического исследования, являющуюся методологической основой остальных отраслей статистики.

Социально-экономическая статистика (Макроэкономическая статистика). Использует методы общей теории статистики, изучает количественную сторону социально-экономических явлений и процессов на уровне национальной экономики.

Математическая статистика и теория вероятности. Изучает случайные величины, законы их распределени.

Международная статистика. Предетом международной статистики является количественная сторона явлений и процессов зарубежных стран и международных организаций.

Отраслевые статистики. Предетом изучения является количественная сторона деятельности различных отраслей экономики (Статистика промышленности, сельского хозяйства).

Общая теория статистики открывает курс изучения статистических дисциплин. Она является основополагающей дисциплиной для изучения отраслевых стастик, создаёт фундамент для усвоения и применения статистических методов анализа.

Общая теория статистики является наукой о наиболее общих принципах и методах статистического исследованиясоциально-экономических явлений и решает другие общественные вопросы. Она разрабатывает систему категорий, рассматривает методы сбора, обобщения и анализа статистических данных.

Общая теория статистики — методологическая основа всех отраслевых статистик.

При изложении основ теории статистики предполагается изучить следующие вопросы:

предмет, методы и задачи статистики и ее связь с экономической теорией и некоторыми другими смежными дисциплинами;

система статистических показателей и классификаций, используемых в экономической статистике, их содержание и область применения, взаимосвязи между показателями и классификациями статистики;

наиболее важные направления статистического анализа, основанного на данных экономики и финансов;

основные источники первичных данных и основы формирования статистической базы.

Предмет статистики — размеры и количественные соотношения качественно определенных социально-экономических явлений, закономерности их связи и развития в конкретных условиях места и времени.

Предмет статистики (статистика изучает):

Массовые общественные явления и их динамику при помощи статистических показателей. Требование массовости обусловлено действием закона больших чисел — при большом количестве наблюдений, действия случайных признаков взаимопогашаются. (численность населения, количество произведенной продукции)

Количественные и качественные явления (Цифровое освещение событий общества).

Количественную сторону общественных явлений в неразрывной связи с их качественным содержанием, наблюдает процесс перехода количественных изменений в качественные (закономерности).

Развитие явления во времени (динамику)

№3.Метод статистики.

Метод статистики и его основные черты.

Специфические приемы и методы статистического изучения массовых явлений

            Статистическое исследование подразделяется на три последовательные стадии:

1) статистическое наблюдение, т.е. сбор первичного статистического материала;

2) сводка и разработка результатов наблюдений, т.е. их обработка;

3) анализ полученных сводных материалов.

На каждой из этих стадий применяются специфические методы, образующие статистическую методологию и обусловленные спецификой предмета статистики.

Метод массовых наблюдений. Поскольку статистика изучает закономерности, проявляющиеся в массовых явлениях под действием закона

больших чисел, то на первой стадии статистического исследования должно быть обеспечено массовое наблюдение, т.е. сбор большого числа отдельных единичных фактов и индивидуальных значений, присущих ему признаков.

Метод группировок. На второй стадии статистического исследования собранные факты подвергаются систематизации и подсчету или сводке. Их делят по признакам различия и объединяют по признакам сходства, иными словами осуществляют группировки. С помощью метода группировок статистики делят изучаемые явления на важнейшие виды, характерные группы и подгруппы по изучаемым признакам.

Методы анализа с помощью обобщающих показателей. На третьей стадии статистического исследования анализируется сводный материал, проявление закономерностей и связей в изучаемых фактах, характеристика типичных их черт. На этой стадии рассчитываются обобщающие показатели (суммарные, относительные и средние величины, статистические коэффициенты).

Анализ с помощью обобщающих показателей заключается в измерении признаков, агрегировании, расчете относительных и средних величин, в сводной оценке вариации признаков, динамике явлений, в применении индексов, в балансовых построениях, в расчете показателей, характеризующих тесноту связей, а также в других приемах.

Все это дополняется табличным методом наиболее рационального изложения цифрового материала и графическим методом - методом наглядного изображения статистических данных.

Статистическая совокупность - это масса отдельных единиц одного и того же вида, объединенных единой качественной основой, но различающихся между собой по ряду признаков.

Например, совокупностью будет население какой-либо страны, которое состоит из отдельных людей, различающихся по полу, возрасту и другим признакам. Однако, она едина в том отношении, что это население одной страны.

Массовые явления всегда представляют собой совокупности единиц, которые в определенном отношении однородны, но в других отношениях различаются между собой.

Статистика характеризует совокупности своими числами-показателями, которые могут быть двоякого рода:

1) показатели, дающие обобщающую характеристику объемов совокупностей. В качестве примера - численность занятых, объемы производства и т.д.

2) показатели, обобщающие характеристики совокупностей по ряду признаков. Например, характеристика населения по результатам переписи: по полу, возрасту, национальности, уровню образования и т.д.

Варьирующие признаки - признаки, принимающие разное значение (качественное или количественное) у отдельных единиц совокупности.

Значение варьирующего признака у отдельных единиц совокупности называется вариантой. Например, рабочие любого предприятия различаются между собой по полу (качественное значение - мужчина или женщина) или по уровню получаемой заработной платы (количественные значения признака) [2, c.54].

Статистика - это обобщающий учет. Статистические цифры дают обобщающую характеристику каким-либо совокупностям фактов, выражая их численность, объем, соотношения частей или среднего уровня с помощью своих признаков. Тем самым она является одним из видов учета, а именно учетом обобщающим, имеющим дело с характеристикой совокупностей, а не единичных фактов.

Статистический показатель - это количественная мера общественных явлений, имеющая качественную определенность.

Нужно различать содержание статистического показателя и его конкретные количественные размеры.

Содержание или качественная определенность показателя характеризует социально-экономическую категорию (население, национальное богатство, объем производства, товарооборот и т.д.). Количественные размеры статистических показателей (т.е. статистические данные) зависят от конкретных условий места и времени.

Например, заработная плата - определенная экономическая категория. Статистика измеряет ее общий объем и средний уровень. Поэтому возникают статистические показатели, характеризующие фонд заработной платы и среднюю заработную плату. В различных условиях и в разное время статистические данные по этим показателям различаются.

Важнейшей задачей статистической науки является разработка методологии расчета статистических показателей. Эти вопросы решаются в рамках отраслевой статистики.

Система статистических показателей. Статистические показатели должны находиться в определенной взаимосвязи между собой, образуя систему взаимосвязанных показателей. В основе системы статистических показателей лежат современная демография, экономическая теория и другие общественные науки.

На международном уровне статистические показатели систематизированы в отдельных руководствах международных организаций: Руководство по СНС, Руководство по государственным финансам, Руководство по банковской и финансовой статистике, Руководство по платежному балансу и др.

Система статистических показателей не является неизменной. В процессе общественного развития одни явления отмирают, другие возникают, что находит отражение в системе показателей.

№4Статистическая совокупность,единица совокупности,качественная однородность,признак:понятие,примеры.

Статистическая совокупность – это множество единиц изучаемого явления, объединенных единой качественной основой, общей связью, но отличающихся друг от друга отдельными признаками. Таковы, например, совокупность домохозяйств, совокупность семей, совокупность предприятий, фирм, объединений и т.п.

Совокупность называется однородной, если один или несколько изучаемых существенных признаков ее объектов являются общими для всех единиц.

Совокупность, в которую входят явления разного типа, считается разнородной. Совокупность может быть однородна в одном отношении и разнородна в другом. В каждом отдельном случае однородность совокупности устанавливается путем проведения качественного анализа, выяснения содержания изучаемого общественного явления.

Единица совокупности — это первичный элемент статистической совокупности, являющийся носителем признаков, подлежащих регистрации, и основой ведущегося при обследовании счета.

Качественная однородность — сходство всех единиц совокупности по какому-либо признаку и несходство по всем остальным.

В статистической совокупности отличия одной единицы совокупности от другой чаще имеют количественную природу. Количественные изменения значений признака разных единиц совокупности называются вариацией.

Вариация признака — количественное изменение признака (для количественного признака) при переходе от одной единицы совокупности к другой.

Признак - это свойство, характерная черта или иная особенность единиц, объектов и явлений, которая может быть наблюдаема или измерена. Признаки делятся на количественные и качественные. Многообразие и изменчивость величины признака у отдельных единиц совокупности называется вариацией.

Атрибутивные (качественные) признаки не поддаются числовому выражению (состав населения по полу). Количественные признаки имеют числовое выражение (состав населения по возрасту).

Показатель — это обобщающая количественно качестванная характеристика какого-либо свойства единиц или совокупности в цельм в конкретных условиях времени и места.

Система показателей — это совокупность показателей всесторонне отражающих изучаемое явление.

Например, изучается зарплата:

Признак — оплата труда

Статистическая совокупность — все работники

Единица совокупности — каждый работник

Качественная однородность — начисленная зарплата

Вариация признака — ряд цифр

№5.Вариация признака,классификация признака.

Признак – свойство, характерная черта или иная особенность единиц (объектов, явлений), которые могут быть наблюдаемы или измерены.

Вариация – различия в значениях того или иного признака у отдельных единиц, входящих в данную совокупность.

 Признак – это качественная особенность единицы совокупности.

По характеру выражения различают атрибутивные и

количественные признаки:

• атрибутивные (описательные) – выражаются словесно, например, пол, национальность, образование и др. По ним можно получить итоговые сведения о количестве статистических единиц, обладающих даннымзначением признака;

• количественные – выражаются числовой мерой (возраст, стаж работы, объем продаж, размер дохода и т.д.) По ним можно получить итоговые данные о количестве единиц, обладающих конкретным значением признака, и суммарное или среднее значение признака по совокупности.

По характеру вариации признаки делятся на:

• альтернативные - могут принимать только одно из двух возможных значений признака. Это признаки обладания или не обладания чем-либо. Например, пол, семейное положение, в маркетинговых или политологических исследованиях - ответ на вопрос в форме «да или нет»;

• дискретные – количественные признаки принимающие только отдельные значения, без промежуточных между ними - как правило целочисленные, например, разряд рабочего, число детей в семье и т.д.);

• непрерывные – количественные признаки, принимающие любые значения. На практике они, как правило, округляются в соответствии с принятой точностью (например: бухгалтерская прибыль по балансу в рублях, налоговая по налоговым регистрам – в тыс. руб.

По отношению ко времени различают:

• моментные признаки, характеризующие единицы совокупности на критический момент временинапример, стоимость основных производственных фондов (ОПФ) определяется на 01.01. и 31.12 соответствующего года как стоимость ОПФ на начало и конец отчётного года;

• интервальные признаки, характеризующие явление за определённый временной период ((год, квартал, месяц и т.д.), например, сменная выработка, дневная выручка, годовой объём продаж и т.д.

По характеру взаимосвязи признаки делятся на:

• факторные, вызывающие изменения других признаков, либо создающие возможности для изменений значений других признаков. Факторные признаки подразделяются соответственно на признаки причины и признаки условия;

• результативные (признаки следствия), зависящие от вариации других признаков. Например, стоимостной объём выпуска продукции является результативным признаком, величина которого зависит от факторных признаков - численности работников и производительности труда.

№6.Статистический показатель,виды статистических показателей.Закон больших чисел.Статистическая закономерность.

Статистический показатель – это количественная оценка свойства изучаемого явления. Статистические показатели можно подразделить на два основных вида: учетно-оценочные показатели (размеры, объемы, уровни изучаемого явления) и аналитические показатели (относительные и средние величины, показатели вариации и т.д.).

Массовый характер общественных законов и своеобразие их действий предопределяет необходимость исследования совокупных данных.

Закон больших чисел порожден особыми свойствами массовых явлений. Последние в силу своей индивидуальности, с одной стороны, отличаются друг от друга, а с другой – имеют нечто общее, обусловленное их принадлежностью к определенному классу, виду. Причем единичные явления в большей степени подвержены воздействию случайных факторов, нежели их совокупность.

Закон больших чисел в наиболее простой форме гласит, что количественные закономерности массовых явлений отчетливо проявляются лишь в достаточно большом их числе.

Таким образом, сущность его заключается в том, что в числах, получающихся в результате массового наблюдения, выступают определенные правильности, которые не могут быть обнаружены в небольшом числе фактов.

Закон больших чисел выражает диалектику случайного и необходимого. В результате взаимопогашения случайных отклонений средние величины, исчисленные для величины одного и того же вида, становятся типичными, отражающими действия постоянных и существенных фактов в данных условиях места и времени.

Тенденции и закономерности, вскрытые с помощью закона больших чисел, имеют силу лишь как массовые тенденции, но не как законы для каждого отдельного случая.

Статистические закономерности изучают распределение единиц статистического множества по отдельным признакам под воздействием всей совокупности факторов.

Статистическая закономерность выступает как объективная закономерность сложного массового процесса и является формой причинной связи. Она обнаруживается в итоге массового статистического наблюдения. Этим обуславливается ее связь с законом больших чисел.

Статистическая закономерность с определенной вероятностью гарантирует устойчивость средних величин при сохранении постоянного комплекса условий, порождающих данное явление.

№7.Задача статистики. Основные функции статистических органов.

 Организация и задачи статистики.

Главным учетно-статистическим центром страны является «Государ-ственный комитет Российской Федерации по статистике» (Госкомстат РФ). Он осуществляет государственное управление делом статистики, учета и отчетности во всех отраслях народного хозяйства и несет всю полноту ответственности за создание и функционирование статистической информации на всех уровнях (государственном, отраслевом, региональном) на основе единой методологии.

Госкомстат РФ разрабатывает табель и формы статистической отчёт-ности, программу единовременных статистических наблюдений, выступает как методологический и руководящий орган осуществления статистической работы.

В областях (краях) статистической работой руководят областные (краевые) статистические управления (комитеты), в районах - отделы по статистике.

Каждое предприятие, организация, учреждение обязано предоставлять достоверную, полную и своевременную информацию в соответствии с утвержденными формами статистической отчетности. Эта работа закреплена за конкретными исполнителями, которые несут административную и юридическую ответственность за качество представляемой информации.

Важнейшей задачей статистики является разработка статистических данных, характеризующих состояние и развитие экономики, культуры, жизненного уровня членов общества, отдельных отраслей, предприятий и т.д.

В условиях рыночной экономики роль статистической службы возрастает, ибо только статистические органы должны и могут организовать сбор и представление пользователям всех уровней системной информации об экономической жизни страны, объединить информацию, собираемую от населения, предприятий и других управленческих и хозяйственных органов. Одной из центральных задач становится статистическое изучение формирования новых отношений собственности, развития новых форм хозяйствования и видов предпринимательской деятельности. Много новых аспектов приобретает социальная статистика - информация об уровне жизни населения, проблема анализа результативности мер по поддержке малообеспеченных слоев населения, занятости населения и пр.

№8.Органы государственной статистики.

осударственная статистика федеральная служба

Федеральная служба государственной статистики (Росстат, ранее Госкомстат) является федеральным органом исполнительной власти, осуществляющим функции по формированию официальной статистической информации о социальном, экономическом, демографическом и экологическом положении страны, а также функции по контролю и надзору в области государственной статистической деятельности на территории Российской Федерации.

Ранее (до марта 2004 года) Федеральная служба государственной статистики называлась Государственный комитет Российской Федерации по статистике и в это же время была произведена передача его функций по принятию нормативных правовых актов в установленной сфере деятельности Министерству экономического развития и торговли Российской Федерации.

Руководство Федеральной службой государственной статистики осуществляет Правительство Российской Федерации.

Процесс реформирования российской статистики был связан с переходом экономики России к рыночным отношениям. Целью реформирования являлись и являются укрепление статистической службы, совершенствование всех элементов статистического наблюдения с учетом новых требований, разработка системы показателей для комплексного анализа переходной экономики, компьютеризация статистики. Поставлена задача создания информационно-телекоммуникационной статистики (ИТСС), в основу которой положено формирование локальных вычислительных сетей (ЛВС), которые будут способствовать переходу к новым информационным технологиям.

Основные функции Федеральной службы государственной статистики являются:

· представление в установленном порядке статистической информации гражданам, Президенту Российской Федерации, Правительству Российской Федерации, Федеральному Собранию Российской Федерации, органам государственной власти, средствам массовой информации, другим организациям, в том числе международным;

· разработка и совершенствование системы статистических показателей, характеризующих состояние экономики и социальной сферы;

· сбор статистической отчетности и формирование на ее основе официальной статистической информации;

· контроль за выполнением организациями и гражданами, осуществляющими предпринимательскую деятельность без образования юридического лица, законодательства Российской Федерации в области государственной статистики;

· развитие информационной системы государственной статистики, обеспечение ее совместимости и взаимодействия с другими государственными информационными системами;

· обеспечение хранения государственных информационных ресурсов и защиты конфиденциальной и отнесенной к государственной тайне статистической информации;

· реализация обязательств Российской Федерации, вытекающих из членства в международных организациях и участия в международных договорах, осуществление международного сотрудничества в области статистики.

· обеспечение и функционирование ЕГРПО (Единого государственного регистра предприятий и организаций);

· сопоставление основных социально-экономических показателей России с аналогичными показателями других стран, совместно с Центробанком составление платежного баланса страны;

· проводит единую техническую политику в области сбора, обработки и передачи статистической информации, в разработке и формировании федеральных программ по вопросам, порученным Росстату.

Государственный статистический учет - это совокупность действий по проведению государственных статистических наблюдений, последующей обработке, анализу, хранению, защите и распространению статистических данных о количественных и качественных характеристиках социально-экономических и демографических явлений и процессов в обществе на основе государственной статистической методологии.

Целью проведения официального статистического учета в Российской Федерации является формирование в соответствии с государственной статистической методологией полной, объективной, актуальной и надежной статистической информации, необходимой для решения стоящих перед нею задач.

№9.Основные направления реформирования статистики.

В настоящее время можно отметить основные направления, по которым должны быть произведены реформы:

соблюдение основного закона статистического учета – гласности и доступности информации при сохранении конфиденциальности индивидуальных показателей (коммерческой тайны);

реформирование методологических и организационных основ статистики: изменение общих задач и принципов ведения хозяйства приводит к изменению теоретических положений науки;

совершенствование системы сбора и обработки информации путем введения таких форм наблюдения, как цензы, регистры (реестры), переписи и др.;

изменение (усовершенствование) методологии исчисления некоторых статистических показателей, характеризующих состояние экономики РФ, с учетом международных стандартов, иностранного опыта ведения статистического учета, систематизация всех показателей и приведение их в порядок, отвечающий вопросам и требованиям времени, с учетом системы национальных счетов (СНС);

обеспечение взаимосвязи статистических показателей, характеризующих уровень развития общественной жизни страны;

учет тенденции компьютеризации.

В ходе реформирования статистической науки должна быть создана единая информационная база (система), которая будет включать в себя информационные базы всех статистических органов, находящихся на более низкой ступени иерархической лестницы организации государственной статистики. В настоящее время проведена большая работа по организации работы статистических органов, но она еще не закончена, и предстоит еще много внимания уделить совершенствованию этого очень важного для государства информационного института.

№10 Понятие о статистическом наблюдении,Основные принципы статистического наблюдения.

Статистическое наблюдение – первый и исходный этап статистического исследования, который представляет собой систематический, планомерно организуемый на научной основе процесс сбора первичных данных о различных явлениях социальной и экономической жизни. Планомерность статистического наблюдения заключается в том, что оно проводится по специально разработанному плану, который включает в себя вопросы, связанные с организацией и техникой сбора статистической информации, контроля ее качества и достоверности, представления итоговых материалов. Массовый характер статистического наблюдения обеспечивается наиболее полным охватом всех случаев проявления изучаемого явления или процесса, т. е. в процессе статистического наблюдения подвергаются измерению и регистрации количественные и качественные характеристики не отдельных единиц изучаемой совокупности, а всей массы единиц совокупности.Систематичность статистического наблюдения означает, что оно должно проводиться не случайным образом, т. е. стихийно, а выполняться либо непрерывно, либо регулярно через равные промежутки времени.

статистическое наблюдение должно быть планомерным, массовым и систематическим.

№11.Подготовка статистического наблюдения.

При подготовке и проведении статистического наблюдения необходимо разрешение ряда вопросов, которые можно разделить на:

1. Программно-методологические; 2. Организационные.

Программно-методологическими вопросами определяются цель статистического наблюдения, устанавливается объект и единица наблюдения, определяется круг признаков, характеризующих единицу наблюдения, по которым производится регистрация данных, или разрабатывается программа.

Программой статистического наблюдения называется перечень вопросов или признаков, на которые должны быть получены ответы по единицам наблюдения. 

Организационные вопросы охватывают сроки и место проведения наблюдения, положения об организационной стороне наблюдения и др.

Цель определяет объект статистического наблюдения. Объект статистического наблюдения представляет совокупность явлений, предметов, процессов и др., охватываемых наблюдением. Объектом может быть население при переписи, предприятия, их персонал и др., т.е. – это исследуемая статистическая совокупность. Она состоит из отдельных единиц. Единица наблюдения представляет собой элемент совокупности, по которому собираются необходимые данные. \

№12.Контроль материалов наблюдения.

Собранные в процессе статистического наблюдения данные о величине признака единиц в изучаемой совокупности должны быть обработаны так, чтобы получился точный и обстоятельный ответ на все вопросы, поставленные с целью исследования. Качество исходного статистического материала предопределяет качество обобщающих показателей, полученных в результате статистической обработки (статистической сводки).

В условиях социалистического хозяйства точность и достоверность материалов статистического наблюдения обеспечивается надлежащим качеством предварительно разработанных программы и плана статистического наблюдения. Однако даже при достаточно совершенной организации статистического наблюдения могут встречаться в полученной статистической информации отдельные ошибки или погрешности, которые следует устранить, чтобы получить доброкачественный исходный статистический материал.

Ошибки статистического наблюдения — расхождение действительных значений признаков единиц наблюдения с их величиной, зарегистрированной в процессе сбора сведений. Ошибки статистического наблюдения разнообразны по происхождению и характеру Они могут заключаться в неполном охвате подлежащих регистрации единиц, в пропуске записи или неясной записи данных по отдельным единицам наблюдения и, наконец, в неправильной записи отдельных ответов (несоответствие их действительным фактам). Ошибки статистического наблюдения возникают часто в связи с отсутствием твердых знаний и „навыков у регистраторов, описками и т. п. В некоторых случаях встречаются и преднамеренные ошибки, которые скрывают или искажают факты; в таких случаях привлекают к ответственности лиц, занятых проведением статистического наблюдения.

Ошибки статистического наблюдения разделяются на категории ь зависимости от источника происхождения и значения ошибок. По источнику происхождения различают ошибки непреднамеренные и преднамеренные, а по значению — случайные и систематические.

Случайными ошибками считаются такие погрешности в записи данных по отдельным единицам, в отношении которых предполагают, что они могут с одинаковой вероятностью исказить результаты статистического наблюдения в противоположные стороны. К ошибкам такого вида относятся непреднамеренные ошибки — как следствие описок или недостаточно ясного понимания регистратором сущности регистрируемых признаков, в частности если регистратор не представляет, какие профессии относятся к категории «рабочие». Случайные ошибки при статистическом наблюдении массы единиц не оказывают существенного влияния на конечные результаты обследования: в процессе статистической сводки собранных данных они обычно взаимопогашаются.

Систематические ошибки искажают сведения по отдельным единицам наблюдения в одном направлении (преувеличивают или преуменьшают). К систематическим ошибкам относятся: пропуски единиц наблюдения, ошибки, возникающие в силу неисправности измерительных приборов, а иногда и стремления отдельных лиц округлять величины при устном опросе. Например, при недокументированном сборе сведений возможны округления возраста, стажа работы, заработной платы. Все систематические ошибки являются преднамеренными ошибками и не погашаются в процессе статистической сводки.

К ошибкам статистического наблюдения относятся ошибки, возникающие в процессе организации выборочного наблюдения, называемые ошибками представительства, или репрезентативности.

Чтобы обеспечить доброкачественность материалов статистического наблюдения, принимают меры для предупреждения ошибок. Основное значение имеет правильная организация статистического наблюдения: разработка плана статистического наблюдения, бланков и инструкций по их заполнению, подбор регистраторов и т. п. /

Чтобы устранить обнаруженные ошибки в материалах статистического наблюдения, производится контроль собранных данных статистического наблюдения — первичного учета.

В условиях все более широкого применения машинной обработки данных статистического наблюдения постепенно их проверку будет осуществлять ЭВМ.

Контроль материалов статистического наблюдения, а также записей в статистической отчетности ведется в двух направлениях. Прежде всего осуществляется счетный, или арифметический, контроль с целью проверки именно счетной согласованности данных, помещенных в формулярах статистического наблюдения, а также правильности подсчета итогов. Например, чтобы проверить, правильность расчета числа рабочих на конец отчетного периода, следует к числу рабочих на начало периода прибавить число поступивших и вычесть число уволенных.

Логический контроль ведется для проверки правильности самого содержания сведений, собранных по каждой единице наблюдения. Логический контроль осуществляется различными способами:

J) сравниваются ответы на различные вопросы одного и того же формуляра, например сопоставляются в бланке переписи населения сведения о профессии, возрасте, семейном положении:

2) сопоставляются записи, относящиеся к отчетному периоду, с аналогичными записями предшествующих периодов или же с плановыми данными отчетного периода;

3) сравниваются фактические данные статистического наблюдения с разработанными нормативами: затрат времени, .удельного расхода материалов и др.;

4) сопоставляются данные проведенных статистических наблюдений с результатами специальных наблюдений выборочного характера, в силу своих особенностей, позволяющих получить более полные данные по отобранной массе единиц.

Особое значение приобретает устранение возникших ошибок в статистической отчетности и документах первичного учета, необходимых для заполнения форм отчетности.

Проверке документов первичного учета и составленной на их основе статистической отчетности уделяется большое внимание на предприятиях отраслей народного хозяйства. Работники ЦСУ СССР и его местных органов, получая статистическую отчетность предприятий и организаций, проверяют полноту поступления и правильность заполнения утвержденных форм отчетности. В случае поступления материалов отчетности не от всех предприятий или наличия в них ошибочных записей принимают меры к устранению ошибок путем повторных запросов, специальных проверок или прямого исключения неверных сведений. В обязанности работников ЦСУ СССР и его местных органов входит также контроль организации первичного учета в организациях и на предприятиях отраслей народного хозяйства СССР.

Собранные в процессе статистического наблюдения данные о каждой единице совокупности подвергаются статистической обработке — статистической сводке, в результате которой получаем в широком смысле слова содержательную, обширную статистическую информацию.

№13.

Виды статистического наблюдения по времени наблюдения.

Виды статистического наблюдения по времени регистрации:

Текущее (непрерывное) наблюдение - проводится для изучения текущих явлений и процессов. Регистрация фактов осуществляется по мере их свершения. (регистрация семейных браков и разводов)

Прерывное наблюдение — проводится по мере необходимости, при этом допускаются временные разрывы в регистрации данных:

Периодическое наблюдение — проводится через сравнительно равные интервалы времени (перепись населения).

Единовременное наблюдение — осуществляется без соблюдения строгой периодичности его проведения

. По времени регистрации фактов наблюдение может быть непрерывным и прерывным. Прерыывное в свою очередь включает периодическое и единовременное. Непре-рыгвное (текущее) наблюдение осуществляется путем непрерывной регистрации фактов по мере их возникновения. При таком наблюдении прослеживаются все изменения изучаемого процесса или явления, что позволяет следить за его динамикой. Непрерывно ведется, например, регистрация органами записи актов гражданского состояния (ЗАГСа) смертей, рождений, браков. На предприятиях ведется текущий учет производства продукции, отпуска материалов со склада и т. д.

Прерывное наблюдение проводится либо регулярно, через определенные промежутки времени (периодическое наблюдение), либо нерегулярно, однократно, по мере необходимости (единовременное наблюдение). В основу периодических наблюдений, как правило, заложены подобные программа и инструментарий, с тем чтобы результаты таких обследований могли быть сопоставимы. Примером периодического наблюдения может являться перепись населения, которая проводится через достаточно длительные промежутки времени, и все формы статистических наблюдений, которые носят ежемесячный, квартальный, полугодовой, годовой и т. д. характер. Единовременное наблюдение характерно тем, что факты регистрируются не в связи с их возникновением, а по состоянию или наличию их на определенный момент или за период времени. Количественное измерение признаков какого-либо явления или процесса происходит в момент проведения обследования, а повторная регистрация признаков может не производиться вообще или сроки ее проведения заранее не определены. Примером единовременного наблюдения может служить единовременное обследование состояния жилищного строительства, которое проводилось в 2000 г.

№14.Виды статистического наблюдения по охвату единиц наблюдения

По степени охвата исследуемой совокупности статистическое наблюдение подразделяется на два вида: сплошное и несплошное. При сплошном (полном) наблюдении охватываются все единицы изучаемой совокупности. Сплошное наблюдение обеспечивает полноту информации об изучаемых явлениях и процессах. Такой вид наблюдения связан с большими затратами трудовых и материальных ресурсов, так как для сбора и обработки всего объема необходимой информации требуется значительное время. Часто сплошное наблюдение вообще невозможно, например, когда обследуемая совокупность слишком велика или отсутствует возможность получения информации обо всех единицах совокупности. По этой причине проводят несплошные наблюдения.

При несплошном наблюдении охватывается только определенная часть изучаемой совокупности, при этом важно заранее определить, какая именно часть изучаемой совокупности будет подвергнута наблюдению и какой критерий будет положен в основу выборки. Преимущество проведения несплошного наблюдения заключается в том, что оно проводится в короткие сроки, связано с меньшими трудовыми и материальными затратами, полученная информация носит оперативный характер. Существует несколько видов несплошного наблюдения: выборочное, наблюдение основного массива, монографическое.

Выборочным называют наблюдение части единиц исследуемой совокупности, выделенной методом случайного отбора. При правильной организации выборочное наблюдение дает достаточно точные результаты, которые можно применить с определенной вероятностью на всю совокупность. Если выборочное наблюдение предполагает отбор не только единиц изучаемой совокупности (выборку в пространстве), но и моментов времени, в которые проводится регистрация признаков (выборка во времени), такое наблюдение называется методом моментных наблюдений.

Наблюдение основного массива охватывает собой обследование определенных, наиболее существенных по значимости изучаемых признаков единиц совокупности. При этом наблюдении в учет принимаются самые крупные единицы совокупности, а регистрируются самые существенные для данного исследования признаки. Например, обследуются 15–20 % крупных кредитных учреждений, при этом регистрируется содержание их инвестиционных портфелей.

Для монографического наблюдения характерно всестороннее и глубокое изучение лишь отдельных единиц совокупности, обладающих какими-либо особенными характеристиками или представляющими какое-либо новое явление. Цель такого наблюдения – выявление имеющихся или только зарождающихся тенденций в развитии данного процесса или явления. При монографическом обследовании отдельные единицы совокупности подвергаются детальному изучению, которое позволяет зафиксировать очень важные зависимости и пропорции, которые не обна-ружимы при других, не столь подробных, наблюдениях. Статистико-монографическое обследование часто применяется в медицине, при обследовании бюджетов семей и т. д. Важно отметить, что монографическое наблюдение тесно связано со сплошным и выборочным наблюдениями. Во-первых, данные массовых обследований необходимы для выбора критерия отбора единиц совокупности для проведения несплошного и монографического наблюдения. Во-вторых, монографическое наблюдение позволяет выявить характерные черты и существенные признаки объекта исследования, уточнить структуру изучаемой совокупности. Полученные выводы можно положить в основу организации нового массового обследования.

№15.Способы статистического наблюдения.

Наряду с видами статистического наблюдения в общей теории статистики рассматриваются способы получения статистической информации, важнейшими из которых являются документальный способ наблюдения, способ непосредственного наблюдения, опрос.

Документальное наблюдение основано на использовании в качестве источника информации данных различных документов, например регистров бухгалтерского учета. Учитывая, что к заполнению таких документов, как правило, предъявляются высокие требования, данные, отраженные в них, носят наиболее достоверный характер и могут служить качественным исходным материалом для проведения анализа.

Непосредственное наблюдение осуществляется путем регистрации фактов, лично установленных регистраторами в результате осмотра, измерения, подсчета признаков изучаемого явления. Таким способом регистрируются цены на товары и услуги, производятся замеры рабочего времени, инвентаризация остатков на складе и т. д.

Опрос базируется на получении данных от респондентов (участников опроса). Опрос применяют в тех случаях, когда наблюдение другими способами не может быть осуществлено. Такой вид наблюдения характерен для проведения различных социологических обследований и опросов общественного мнения. Статистическая информация может быть получена разными видами опросов: экспедиционным, корреспондентским, анкетным, явочным.

Экспедиционными (устный) опрос проводится специально подготовленными работниками (регистраторами), которые фиксируют ответы респондентов в формулярах наблюдения. Формуляр представляет собой бланк документа, в котором необходимо заполнить поля для ответов.

Корреспондентский опрос предполагает, что на добровольной основе штат респондентов сообщает сведения непосредственно в орган, ведущий наблюдение. Недостатком этого способа является то, что затруднительно проверить правильность полученной информации.

При анкетном опросе респонденты заполняют анкеты (вопросники), добровольно и преимущественно анонимно. Поскольку этот способ получения информации не является надежным, его применяют в тех исследованиях, где не требуется высокая точность результатов. В некоторых ситуациях бывает достаточно приближенных результатов, которые улавливают лишь тенденцию и фиксируют появление новых фактов и явлений. Явочный опрос предполагает представление сведений в органы, ведущие наблюдение, в явочном порядке. Таким способом регистрируются акты гражданского состояния: браки, разводы, смерти, рождения и т. д.

№16.Формы организации статистического наблюдения.

формы статистического наблюдения: отчетность, специально организованное статистическое наблюдение, регистры.

Статистическая отчетносты – основная форма статистического наблюдения, которая характеризуется тем, что сведения об изучаемых явлениях статистические органы получают в виде особых документов, представляемых предприятиями и организациями в определенные сроки и по установленной форме. Сами формы статистической отчетности, методы сбора и обработки статистических данных, методология статистических показателей, установленные ФСГС, являются официальными статистическими стандартами РФ и обязательны для всех субъектов общественных отношений.

Статистическую отчетность делят на специализированную и типовую. Состав показателей типовой отчетности един для всех предприятий и организаций, в то время как состав показателей специализированной отчетности зависит от специфики отдельных отраслей экономики и сферы

деятельности. По срокам представления статистическая отчетность бывает ежедневная, недельная, декадная, двухнедельная, месячная, квартальная, полугодовая и годовая. Статистическая отчетность может передаваться по телефону, каналам связи, на электронных носителях с обязательным последующим представлением на бумажных носителях, скрепленная подписью ответственных лиц.

Специально организованное статистическое наблюдение представляет собой организуемый статистическими органами сбор сведений или для изучения явлений, не охватываемых отчетностью, или для более глубокого изучения отчетных данных, их проверки и уточнения. Различного рода переписи, единовременные обследования являются специально организованными наблюдениями.

Регистры – это такая форма наблюдения, при которой факты состояния отдельных единиц совокупности непрерывно регистрируются. Наблюдая за единицей совокупности, предполагают, что происходящие там процессы имеют начало, долговременное продолжение и конец. В регистре каждая единица наблюдения характеризуется совокупностью показателей. Все показатели хранятся до тех пор, пока единица наблюдения находится в регистре и не закончила своего существования. Некоторые показатели остаются неизменными все время, пока единица наблюдения находится в регистре, другие могут меняться время от времени. Примером такого регистра может служить Единый государственный регистр предприятий и организаций (ЕГРПО). Все работы по его ведению осуществляет ФСГС.

Итак, выбор видов, способов и форм статистического наблюдения зависит от целого ряда факторов, основными из которых являются цели и задачи наблюдения, специфика наблюдаемого объекта, срочность представления результатов, наличие подготовленных кадров, возможность применения технических средств сбора и обработки данных.

№18.Понятие статистической группировки.Виды статистических группировок.

Статистическая группировка – это деление изучаемой совокупности на группы по каким-либо признакам. 

Метод группировок решает следующие задачи:

1.

Выделение социально-экономических типов явлений;

2.

Изучение структуры совокупности и структурных сдвигов;

3.

Выявление наличия, направления и формы связи между факторным и результативным признаками.

Виды группировок в зависимости от решаемых ими задач:

1. Типологические – это разделение единиц совокупности, как правило по качественному признаку на социально-экономические типы. 

2. Структурные – это разделение единиц совокупности на группы, характеризующие ее структуру.

3. Аналитические – это разделение единиц совокупности на группы по факторному признаку с целью определения наличия, направления и формы связи между факторным и результативным признаками. 

Виды группировок по числу группировочных признаков:

1. Простые – деление единиц совокупности на группы проводится по одному признаку.

2. Комбинированные (сложные) – деление единиц совокупности на группы проводится по 2 и более признакам (как правило, 2-4 признака). 

3. Многомерные - деление единиц совокупности на группы проводится по множеству признаков методами кластерного анализа на ЭВМ. 

Особым видом группировок является классификация. Классификация – это общепринятая, нормативная группировка. Классификации узаконены, отражаются в нормативных документах, устанавливаются в определенном виде органами государственной и международной статистики и становятся общепринятыми стандартами. Примером классификаций, используемых в экономике, являются классификации отраслей, земельных угодий, основных фондов, населения по статусу занятости и т.д

№19Группировочный признак,построение группировки по количественному и качественному признакам.Классификация сходство и различие группировками.

Чаще всего простые итоговые сводки не удовлетворяют исследователя, так как они дают слишком общие представления об изучаемом явлении. Поэтому статистический материал подвергается группировке.

Группировка — это метод, при котором вся исследуемая совокупность разделяется на группы по какому-то существенному признаку. Например, группировка предприятий по формам собственности или группировка населения по размеру среднедушевого дохода.

Группировка создаёт основу для последующей сводки и анализа данных.

Третий этап статистического исследования состоит в том, что с помощью обобщающих обобщающих статистических показателей: относительных и средних величин, показателей вариации и динамики, экономических индексов, а также с помощью табличного и графического методов осуществляется анализ полученных данных.

Группировка статистических данных

Группировка — это метод, при котором вся исследуемая совокупность разделяется на группы по какому-то существенному признаку.

Признак, по которому осуществляется группировка называется группировочным признаком или основанием группировки.

Группировка представляет собой способ подразделения рассматриваемой совокупности данных на однородные по изучаемым признакам группы. Это делается с целью изучения структуры этой совокупности либо взаимосвязей между отдельными элементами этой совокупности. С помощью группировки можно выявить влияние отдельных единиц на средние итоговые показатели. Так, например, группировка рабочих данной организации по уровню производительности труда используется с целью выявления влияния высокой производительности труда отдельных рабочих на среднюю производительность по организации и для определения резерва, кроющегося в повышении производительности труда всех рабочих до уровня передовых рабочих.

Как будет показано в статьях данного сайта, наибольшее распространение в экономическом анализе имеет группировка по факторам, связанным:

с трудовыми ресурсами, т.е. с живым трудом;

со средствами труда, т.е. с основными производственными фондами;

с предметами труда, т.е. с материальными ресурсами.

Эти три группы факторов оказывают влияние на объем продукции, выпускаемой данной организацией.

Виды группировок

Выбор группировочного признака зависит от цели данной группировки и предварительного экономического анализа явления.

В зависимости от степени сложности массового явления и задач анализа - группировки могут производится по одному или нескольким признакам:

Если производится группировка только по одному признаку, то она называется простой.

Если по двум и более признакам, то такая группировка называется сложной или комбинационной.

В зависимости от решаемых задач различают типологические, структурные и аналитические группировки:

Типологическая группировка — представляет собой разделение исследуемой совокупности на однородные группы. (группировка предприятий по формам собственности)

Структурная группировка — группировка, в которой происходит разделение однородной совокупности на группы, характеризующие ее структуру по какому-то варьирующему признаку. (группировка населения по уровню дохода). Анализ статистических данных структурных группировок, взятых за ряд периодов показывает изменение структуры изучаемых явлений, то есть структурные сдвиги.

Аналитическая (факторная) группировка — позволяет выявить взаимосвязи между изучаемыми явлениями и их признаками. (группировка банков по сумме уставного капитала, величине активов и балансовой прибыли)

В процессе проведения экономического анализа, как правило, применяются два основных вида группировок:структурные и аналитические.

Структурные группировки используются с целью исследования состава и структуры совокупности данных, а также с целью изучения тех изменений в этой совокупности, которые имеют место в соответствии с выбранным изменяющимся признаком.

Аналитические же группировки используются для исследования взаимных связей, существующих между показателями, характеризующими рассматриваемую совокупность данных. В этих условиях один из показателей является обобщающим, результативным, а другие показатели рассматриваются как факторы, влияющие на обобщающий показатель.

№20.Интервал.Понятие,составляющие интервала,виды интервалов.Определение оптимального количества групп.

Определение интервала группировки.

Интервал — значения варьирующего признака, лежащие в определенных границах. Каждый интервал имеет свою величину, верхнюю и нижнюю границы или хотя бы одну из них. Нижней границей называется наименьшее значение признака в интервале, а верхней — наибольшее значение признака в нем. Величина интервала — разность между верхней и нижней границами интервала.

Интервалы группировки в зависимости от их величины бывают равные и неравные. Последние делятся на прогрессивно возрастающие, прогрессивно убывающие, произвольные и специализированные.

Если вариация признака проявляется в сравнительно узких границах и распределение носит более или менее равномерный характер, то строят группировку с равными интервалами.

Величина равного интервала определяется по следующей формуле:

Прежде чем определять размах вариации, из совокупности рекомендуется исключить аномальные наблюдения (крайние точки).

Полученная величина является шагом интервала.

Открытые интервалы — те, у которых указана только одна граница.

Закрытые интервалы — те, у которых обозначены обе границы.

Ширина открытого интервала принимается равной ширине соседнего с ним закрытого интервала.

Ширина открытого интервала принимается равной ширине соседнего с ним закрытого интервала.

Виды группировок. Определение числа групп, величины интервалов В зависимости от решаемых задач выделяют следующие виды группировок: 1) типологическая, 2) структурная, 3) аналитическая. Типологическая группировка – это разделение исследуемой качественно разнородной совокупности на классы, социально-экономические типы, однородные группы единиц. Например, группировка промышленных предприятий по формам собственности. Структурной называется группировка, в которой происходит разделение однородной совокупности на группы, характеризующие её структуру по какому-либо варьирующему признаку. С помощью таких группировок могут изучаться: состав населения по полу, возрасту, месту проживания; состав предприятий по численности занятых, стоимости основных фондов и т.д. Группировка, выявляющая взаимосвязи между изучаемыми явлениями и их признаками, называется аналитической группировкой. Взаимосвязь проявляется в том, что с возрастанием значения факторного признака систематически возрастает или убывает среднее значение результативного признака. Например, производительность труда зависит от технического уровня предприятия: чем он выше, тем при прочих равных условиях выше производительность труда занятых на предприятии. Поэтому, группируя промышленные предприятия, производящие одну и ту же продукцию, по техническому уровню производства (фондовооружённости труда) и исчисляя для каждой группы среднюю выработку продукции на одного работающего, можно статистически отразить эту зависимость между факторами. Особенности аналитической группировки следующие: во-первых, в основу группировки кладётся факторный признак; во-вторых, каждая выделенная группа характеризуется средними значениями результативного признака. В зависимости от количества группировочных признаков различают простую и  комбинационную (сложную).   Простая группировка – распределение совокупности по одному признаку.  Например, группировка рабочих предприятия по стажу работы. Комбинационная группировка – распределение совокупности по двум и более признакам.  Например, группировка рабочих предприятия по стажу работы и размеру заработной платы. В зависимости от характера группировочного признака группировка может быть качественная и количественная. Качественная группировка – распределение совокупности по атрибутивному признаку, выражающемуся словом.  Например, группировка рабочих по полу. Количественная группировка – распределение совокупности по числовому признаку.  Например, группировка рабочих по размеру заработной платы. Этот вид группировки может быть в дискретной и интервальной форме. При этом интервалы могут быть открытые (если указана только одна из границ) и закрытые, равные (если их шаг одинаков) и неравные. Наиболее наглядны равные закрытые интервалы. При группировке с закрытыми интервалами верхнюю границу не включают в интервал, а нижнюю включают. Принципы построения статистических группировок. После определения основания группировки следует решить вопрос о количестве групп, на которые надо разбить исследуемую совокупность. Число групп зависит от задач исследования, вида приз, положенного в основание группировки, численности совокупности, степени вариации признака. Для определения оптимального числа групп применяется формула Стерджесса: , где n – число групп; N – число единиц совокупности. n округляют до целого числа. После определения числа групп следует определить интервалы группировки. Интервал – это значения варьирующего признака, лежащие в определённых границах. Нижней границей интервала называется наименьшее значение признака в интервале, а верхней границей – наибольшее значение признака в нём. Величина (ширина) интервала представляет собой разность между верхней и нижней границами интервала. Интервалы группировки в зависимости от их величины бывают равные и неравные. Если вариация признака проявляется в сравнительно узких границах и распределение носит более или менее равномерный характер, то строят группировку с равными интервалами. Величину равного интервала определяют по формуле: , где и – максимальное и минимальное значения признака Открытые – это интервалы, у которых указана только одна граница: верхняя – у первого интервала, нижняя – у последнего. Ширина открытого интервала принимается равной ширине смежного с ним интервала. Закрытыми называются интервалы, у которых обозначены обе границы. При группировке по количественному признаку границы интервалов могут быть обозначены по-разному. Если основанием группировки выступает непрерывный признак, то одно и то же значение признака выступает и верхней, и нижней границами у двух смежных интервалов. Т.о., верхняя граница i-го интервала равна нижней границе i+1-го интервала. При таком обозначении границ может возникнуть вопрос, в какую группу включать единицы объекта, значения признака у которых совпадают с границами интервалов. Обычно нижняя граница формируется по принципу «включительно», а верхняя – по принципу «исключительно». Если в основании группировки лежит дискретный признак, то нижняя граница i-го интервала равна верхней границе i-1-го интервала, увеличенной на 1. Неравные интервалы применяются в статистике, когда значения признака варьируют неравномерно и в значительных размерах.

№21.Виды рядов распределения и их элементы.

^ Ряды распределения. Понятие, элементы ряда распределения, виды рядов распределения

После определения группировочного признака, количества групп и интервалов группировки данные сводки и группировкипредставляются в виде рядов распределения и оформляются в виде статистических таблиц.

Ряд распределния является одним из видов группировок.

^ Ряд распределения — представляет собой упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку.

В зависимости от признака, положенного в основу образования ряда распределения различают атрибутивные и вариационные ряды распределения:

Атрибутивными — называют ряды распределения, построенные по качественными признакам.

Ряды распределения, построенные в порядке возрастания или убывания значений количественного признака называютсявариационными.

^ Вариационный ряд распределения состоит из двух столбцов:

В первом столбце приводятся количественные значения варьирующегося признака, которые называются вариантами и обозначаются  . Дискретная варианта — выражается целым числом. Интервальная варианта находится в пределах от и до. В зависимости от типа варианты можно построить дискретный или интервальный вариационный ряд.

Во втором столбце содержится количество конкретных вариант, выраженное через частоты или частости:

Частоты — это абсолютные числа, показывающие столько раз в совокупности встречается данное значение признака, которые обозначают  . Сумма всех частот равна должна быть равна численности единиц всей совокупности.

Частости ( ) — это частоты выраженные в процентах к итогу. Сумма всех частостей выраженных в процентах должна быть равна 100% в долях единице.

Графическое изображение рядов распределения

Наглядно ряды распределения представляются при помощи графических изображений.

Ряды распределения изображаются в виде:

Полигона

Гистограммы

Кумуляты

Огивы

№ 22.Графическое изображение рядов распределения.

Ряды распределения, их виды и графическое изображение.

Построение рядов распределения является составным элементом сводки данных статистического наблюдения. Они представляют собой группировку, где известна численность единиц в группах или удельный вес группы в общем итоге. По форме это простейшая разновидность структурной группировки по одному признаку в групповой таблице с двумя графами: группы по выделенному признаку и численности групп. Численные значения признака в рядах распределения называются вариантами, а численность каждой группы – частотами (обычно обозначаются буквой f). Сумма всех частот определяет численность всей совокупности, или ее объем (это обычно n). Численности групп, выраженные в долях от общей численности единиц, называются частостями и обозначаются буквой w. Сумма частостей равна 1, если они выражены в ее долях, и 100%, если они выражены в процентах.

Ряды распределения подразделяются на атрибутивные (группировка по атрибутивным признакам) и вариационные (по количественным признакам). По характеру вариации признака различают вариационные ряды распределения прерывные (дискретные) и непрерывные (интервальные). В первом случае признак изменяется прерывно, т.е. через определенное число единиц. Во втором группировочный признак в определенном интервале может принимать любые значения. 

Анализ рядов распределения сопровождается их графическим изображением. Именно графики лучше всего позволяют судить о форме распределения. Для отображения вариационных рядов распределения используются следующие графики: полигон, гистограмму и кумуляту.Полигон применяют для графического изображения дискретного вариационного ряда, и этот график является разновидностью статистических ломаных. В прямоугольной системе координат по оси абсцисс откладываются варианты признака, а по оси ординат – частости каждого варианта. На пересечении абсциссы и ординаты фиксируют точки, соответствующие данному ряду распределения. Соединив эти точки прямыми, получим ломаную, которая и является полигоном, или эмпирической кривой распределения. Для замыкания полигона крайние вершины соединяют с точками на оси абсцисс, отстоящими на одно деление в принятом масштабе, или с серединами предыдущего (перед начальным) и последующим (за последним) интервалов.

Рисунок 1. Графическое изображение полигона

 Гистограмма применяется для графического изображения непрерывных (интервальных) вариационных рядов. При этом на оси абсцисс откладывают интервалы ряда. На этих отрезках строят прямоугольники, высота которых по оси ординат в принятом масштабе соответствует частотам. При равных интервалах по оси абсцисс откладывают прямоугольники, сомкнутые друг с другом, с равными основаниями и ординатами, пропорциональными весам. Данный ступенчатый многоугольник и называется гистограммой. Его построение аналогично построению столбиковых диаграмм. Гистограмма может быть преобразована в полигон распределения, для чего середины верхних сторон прямоугольников соединяют отрезками прямых. Две крайние точки прямоугольников замыкают по оси абсцисс на середине интервалов аналогично замыканию полигона. В случае неравенства интервалов график строится не по частотам или частостям, а по плотности распределения (отношению частот или частостей к величине интервала), и тогда высоты прямоугольников графика будут соответствовать величинам этой плотности.

Рисунок 2. Графическое изображение гистограммы

Кумулята изображает кумулятивные ряды распределения, где по оси абсцисс откладывают варианты признака, а по оси ординат – накопленные частоты или частости. Полученные точки соединяют прямыми, образующими кумуляту. При построении кумуляты интервального ряда распределения нижней границе первого интервала соответствует частота, равная нулю, а верхней границе – вся частота данного интервала. Верхней границе второго интервала соответствует накопленная частота, равная сумме частот первых двух интервалов, и т.д. Другой формой кумулятивного ряда распределения является огива, в графике которой накопленные частоты берутся в обратном порядке, т.е. от наибольшего к наименьшему значению изучаемого признака.

Рисунок 3. Графическое изображение кумуляты

 

№23 понятие о статистической таблице.

Особое место в статистике занимает табличный метод, который имеет универсальное значение. С помощью статистических таблиц осуществляется представление данных результатов статистического наблюдения, сводки игруппировки. Поэтому обычно статистическая таблица определяется как форма компактного наглядного представления статистических данных.

Анализ таблиц позволяет решать многие задачи при изучении изменения явлений во времени, структуры явлений и их взаимосвязей. Таким образом, статистические таблицы выполняют роль универсального средства рационального представления, обобщения и анализа статистической информации.

Внешне статистическая таблица представляет собой систему построенных особым образом горизонтальных строк и вертикальных столбцов, имеющих общий заголовок, заглавия граф и строк, на пересечении которых и записываются статистические данные.

Каждая цифра в статистических таблицах — это конкретный показатель, характеризующий размеры или уровни, динамику, структуру или взаимосвязи явлений в конкретных условиях места и времени, то есть определенная количественно-качественная характеристика изучаемого явления.

Если таблица не заполнена цифрами, то есть имеет только общий заголовок, заглавия граф и строк, то мы имеем макет статистической таблицы. Именно с его разработки и начинается процесс составления статистических таблиц.

Основными элементами статистической таблицы являются подлежащее и сказуемое таблицы.

Подлежащее таблицы — это объект статистического изучения, то есть отдельные единицы совокупности, их группы или вся совокупность в целом.

Сказуемое таблицы — это статистические показатели, характеризующие изучаемый объект.

Подлежащее и показатели сказуемого таблицы должны быть определены очень точно. Как правило подлежащее распологается в левой части таблицы и составляет содержание строк, а сказуемое — в правой части таблицы и составляет содержание граф.

Обычно при расположении показателей сказуемого в таблице придерживаются следующего правила: сначала приводят абсолютные показатели, характеризующие объем изучаемой совокупности, затем — расчетные относительные показатели, отражающие стркутуру, динамику и взаимосвязи между показателями.

Построение аналитических таблиц

Построение аналитических таблиц таково. Любая таблица состоит из подлежащего и сказуемого. Подлежащее раскрывает экономическое явление, о котором идет речь в данной таблице и содержит набор показателей, отображающих это явление. Сказуемое таблицы поясняет, какие именно признаки отображают подлежащее.

Некоторые таблицы отражают изменения структуры каких-либо экономических показателей. В таких таблицах помещается информация о составе анализируемого экономического явления как в базисном, так и в отчетном периоде. По этим данным определяется доля (удельный вес) каждой части в общей совокупности и рассчитываются отклонения от базисных удельных весов по каждой части.

Отдельные таблицы могут отражать взаимосвязь между экономическими показателями по каким-либо признакам. В подобных таблицах информация по данному экономическому показателю располагается в порядке возрастания или убывания числовых величин, характеризующих этот показатель.

В экономическом анализе составляются также таблицы, отражающие результаты определения влияния отдельных факторов на величину анализируемого обобщающего (результативного) показателя. При оформлении подобных таблиц вначале помещают информацию о факторах, влияющих на обобщающий показатель, затем информацию о самом обобщающем показателе и наконец об изменении этого показателя в совокупности, а также за счет воздействия каждого анализируемого фактора. Отдельные аналитические таблицы отражают результаты подсчета резервов улучшения экономических показателей, выявленные в результате проведенного анализа. В таких таблицах показывается как фактический, так и теоретически возможный размер влияния отдельных факторов, а также возможная величина резерва роста обобщающего показателя за счет влияния каждого отдельного фактора.

Наконец, в анализе хозяйственной деятельности составляются также таблицы, которые предназначены для обобщения результатов проведенного анализа.

Практикой статистики разработаны следующие правила составления таблиц:

Таблица должна быть выразительной и компактной. Поэтому вместо одной громозкой таблицы по множеству признаков лучше сделать несколько небольших по объему, но наглядных, отвечающих задаче исследования таблиц.

Название таблицы, заглавия граф и строк следует формулировать точно и лаконично.

В таблице обязательно должны быть указаны: изучаемый объект, территория, и время к которым относятся приводимые в таблице данные, единицы измерения.

Если какие-то данные отсутствуют, то в таблице либо ставят многоточие, либо пишут "нет сведений", если какое-то явление не имело места, то ставят тире

Значения одних и тех же показателей приводятся в таблице с одинаковой степенью точности.

Таблица должна иметь итоги по группам, подгруппам и в целом. Если суммирование данных невозможно, то в этой графе ставят знак умножения "*".

В больших таблицах после каждых пяти строк деляют промежуток, чтобы было удобнее читать и анализировать таблицу.

№ 24.Основные правила построения таблиц.Чтение и анализ статистических таблиц.

Среди методов экономического анализа наиболее распространен табличный метод (способ) отображения исследуемых цифровых данных. Дело в том, что как исходные данные для проведения анализа, так и различные расчеты, а также результаты проведенного исследования оформляются в виде аналитических таблиц. Таблицы представляют собой весьма целесообразную и наглядную форму отображения числовой информации, используемой в анализе хозяйственной деятельности. В аналитических таблицах в определенном порядке располагается цифровая информация об изучаемых экономических явлениях. Табличный материал гораздо более информативен и нагляден по сравнению с текстовым изложением материала. Таблицы позволяют представить аналитические материалы в виде единой целостной системы.

Вид статистической таблицы определятеся характером разработки показателей ее полежащего.

Различают три вида статистических таблиц:

простые

групповые

комбинационные

Простые таблицы содержат перечень отдельных единиц, входящих в состав совокупности анализируемого экономического явления. В групповых таблицах цифровая информация в разрезе отдельных составных частей исследуемой совокупности данных объединяется в определенные группы в соответствии с каким-либо признаком.Комбинированные таблицы содержат отдельные группы и подгруппы, на которые подразделяются экономические показатели, характеризующие изучаемое экономическое явление. При этом такое подразделение осуществляется не по одному, а по нескольким признакам. в групповых таблицах осуществляется простая группировка показателей, а в комбинированных — комбинированная группировка. Простые таблицы вообще не содержат никакой группировки показателей. Последний вид таблиц содержит лишь несгруппированный набор сведений об анализируемом экономическом явлении.

Простые таблицы

Простые таблицы имеют в подлежащем перечень единиц совокупности, времени или территорий.

Добыча некоторых видов ископаемых в России в 2007 г.

Виды продукции

Произведено

Нефть млн.т

491

Естественный газ млрд. куб.м

651

Уголь млн.т.

315

Групповые таблицы

Групповыми называются таблицы, имеющие в подлежащем группировку единиц совокупности по одному признаку.

Распределение населения России по полу на 1 января 2007 г.

млн.чел

в % к итогу

Численность населения — всего

142,0

100,0

В том числе:

Мужчины

65,8

46,3

Женщины

76,4

53,7

Комбинационные таблицы

Комбинационные таблицы имеют в подлежащем группировку единиц совокупности по двум или более признакам.

Внешняя торговля РФ в 2007 г. (в фактически действовавших ценах)

млрд.долл США

в % к итогу

Экспорт товаров

355,2

100

со странами дальнего зарубежья

301,5

84,9

со странами СНГ

53,7

15,1

Импорт товаров

223,1

100

со странами дальнего зарубежья

191,2

85,7

со странами СНГ

31,9

14,3

По характеру разработки показателей сказуемого различают:

таблицы с простой разработкой показателей сказуемого, в которых имеет место параллельное расположение показателей сказуемого.

таблицы со сложной разработкой показателей сказуемого, в которых имеет место комбинирование показателей сказуемого: внутри групп, образованных по одному признаку, выделяют подгруппы по другому признаку.

Таблица с простой разработкой показателей сказуемого

Отделения

Численность студентов, чел.

В том числе

по полу

в возрасте, лет

мужчины

женщины

до 20

20-23

23 и более

А

1

2

3

4

5

6

Дневное

1200

400

800

860

120

220

Вечернее

800

300

500

320

180

300

Всего

2000

700

1300

1180

300

520

В сказуемом этой таблицы приводятся данные сначала о распределении студентов по полу, а затем — по возрасту, т.е. имеют место изолированные характеристики по двум признакам.

Таблица со сложной разработкой показателей сказуемого

Отделения

Численность студентов, чел.

В том числе

мужчины

женщины

Всего

из них в возрасте, лет

Всего

из них в возрасте, лет

до 20

20-23

23 и более

до 20

20-23

23 и более

А

1

2

3

4

5

6

7

8

9

Дневное

1200

400

260

50

90

800

600

70

130

Вечернее

800

300

110

80

110

500

210

100

190

Всего

2000

700

370

130

200

1300

810

170

320

Сказуемое этой таблицы не только характеризует распределение студентов по каждому из двух выделенных признаков, но и позволяет изучить состав каждой группы, выделенной по одному признаку — полу, по другому признаку — возрасту студентво, т.е. имеет место комбинирование двух признаков.

Следовательно, таблицы со сложной разработкой показателей сказуемого обеспечивают более широкие возможности для анализа изучаемых показателей и взаимосвязей между ними. Простую и сложную разработку показателей сказуемого может иметь таблица любого вида: простая, групповая, комбинационная.

В зависимости от этапа статистического исследования таблицы делятся на:

разработочные (вспомогательные), цель которых обобщить информацию по отдельным единицам совокупности для получения итоговых показателей.

сводные, задача которых показать итоги по группам и всей совокупности в целом.

аналитические таблицы, задача которых — расчет обобщающих характеристик и подготовка информационной базы для анализа и структуры и структурыных сдвигов, динамики изучаемых явлений и взяимосвязей между показателями.

Итак, мы рассмотрели табличный метод отображения исследуемых цифровых данных, широко используемый в ходе проведения анализа экономических явлений, статистических данных и хозяйственной деятельности организаций.

№25 Понятие о статистическом графике.Элементы графика.

Статистический график - это чертеж, на котором статистические совокупности, характеризуемые определенными показателями, описываются с помощью условных геометрических образов или знаков. Представление данных таблицы в виде графика производит более сильное впечатление, чем цифры, позволяет лучше осмыслить результаты статистического наблюдения, правильно их истолковать, значительно облегчает понимание статистического материала, делает его наглядным и доступным. Это, однако, вовсе не означает, что графики имеют лишь иллюстрированное значение. Они дают новое знание о предмете исследования, являясь методом обобщения исходной информации. 

При построении графического изображения следует соблюдать ряд требований. Прежде всего график должен быть достаточно наглядным, так как весь смысл графического изображения в том и состоит, чтобы наглядно изобразить статистические показатели. Кроме того, график должен быть выразительным, доходчивым и понятным. Для выполнения вышеперечисленных требований каждый график должен включать ряд основных элементов: графический образ; поле графика; пространственные ориентиры; масштабные ориентиры; экспликацию графика. 

Графический образ - это геометрические знаки, т.е. совокупность точек, линий, фигур, с помощью которых изображаются статистические показатели. 

Поле графика - это часть плоскости, где расположены графические образы. Поле графика имеет определенные размеры, которые зависят от его назначения. 

Пространственные ориентиры графика задаются в виде системы координатных сеток. Система координат необходима для размещения геометрических знаков в поле графика. 

Масштабные ориентиры статистического графика определяются масштабом и системой масштабных шкал. Масштаб статистического графика - это мера перевода числовой величины в графическую. 

Масштабной шкалой называется линия, отдельные точки которой могут быть прочитаны как определенные числа. Шкала имеет большое значение в графике и включает три элемента: линию (или носитель шкалы), определенное число помеченных черточками точек, которые расположены на носителе шкалы в определенном порядке, цифровое обозначение чисел, соответствующих отдельным помеченным точкам. 

№26 Виды статистических графиков.

Классификация видов графиков

Существует множество видов графических изображений (рис. 5.5 и 5.6). Их классификация основана на ряде признаков:

1. способ построения графического образа;

2. геометрические знаки, изображающие статистические показатели;

3. задачи, решаемые с помощью графического изображения.

Рис. 5.5. Классификация статистических графиков по форме графического образа

По способу построения статистические графики делятся на диаграммы и статистические карты.

Диаграммы - наиболее распространенный способ графических изображений. Это графики количественных отношений. Виды и способы их построения разнообразны. Диаграммы применяются для наглядного сопоставления в различных аспектах (пространственном, временном и др.) независимых друг от друга величин: территорий, населения и т. д. При этом сравнение исследуемых совокупностей производится по какому-либо существенному варьирующему признаку.

Рис. 5.6. Классификация статистических графиков по способу построения и задачам изображения

Статистические карты - графики количественного распределения по поверхности. По своей основной цели они близко примыкают к диаграммам и специфичны лишь в том отношении, что представляют собой условные изображения статистических данных на контурной географической карте, т. е. показывают пространственное размещение или пространственную распространенность статистических данных.

Геометрические знаки, как было сказано выше, - это либо точки, либо линии или плоскости, либо геометрические фигуры. В соответствии с этим различают графики точечные, линейные, плоскостные и пространственные (объемные).

При построении точечных диаграмм в качестве графических образов применяются совокупности точек; при построении линейных - линии. Основной принцип построения всех плоскостных диаграмм сводится к тому, что статистические величины изображаются в виде геометрических фигур и, в свою очередь, подразделяются на

столбиковые,

полосовые,

круговые,

квадратные,

фигурные.

Статистические карты по графическому образу делятся на

картограммы

картодиаграммы.

В зависимости от круга решаемых задач выделяют

диаграммы сравнения,

структурные диаграммы

диаграммы динамики.

Особым видом графиков являются диаграммы распределения величин, представленных вариационным рядом. Это гистограмма, полигон, огива, кумулята.

№27.Абсолютные величины и их показатели.

Статистические данные, полученные при наблюдении, в результате сводки, группировки, почти всегда являются абсолютными величинами, т. е. величинами, которые выражены в натуральных единицах и получены в результате счета или непосредственного измерения. Абсолютные величины отражают численность единиц изучаемых совокупностей, размеры или уровни признаков зарегистрированных у отдельных единиц совокупности, и общий объем количественно выраженного признака как результат суммирования всех его отдельных значений.

Абсолютные величины имеют большое познавательное значение.

Абсолютные величины выражают размеры (уровни, объемы) социально–экономических явлений и процессов, их получают в результате статистического наблюдения и сводки исходной информации. Абсолютные величины используют в практике торговли, применяют в анализе и прогнозировании коммерческой деятельности. На основе этих величин в коммерческой деятельности составляют хозяйственные договоры, оценивают объем спроса на конкретные изделия и т. д. Абсолютными величинами измеряются все стороны общественной жизни.

Абсолютные величины по способу выражения размеров изучаемых процессов подразделяются на: индивидуальные и суммарные, они в свою очередь относятся к одному из видов обобщающих величин. Размеры количественных признаков у каждой статистической единицы характеризуют индивидуальные абсолютные величины, а также они являются базой при статистической сводке для соединения отдельных единиц статистического объекта в группы. На их основе получают абсолютные величины, в которых можно выделить показатели объема признаков совокупности и показатели численности совокупности. Если заняться исследованием развития торговли и ее состояния в определенном районе, то определенное количество фирм можно отнести к индивидуальным величинам, а объем товарооборота и число работников, работающих в фирме, относят к суммарным.

Абсолютные величины бывают экономически простыми (численность магазинов, работников) и экономически сложными (объем товарооборота, размер основных фондов).

Абсолютные величины – всегда числа именованные, имеют определенную размерность, единицы измерения. В статистической науке применяются натуральные, денежные (стоимостные) и трудовые единицы измерения.

Единицы измерения называют натуральными, если они будут соответствовать потребительским или природным свойствам предмета, товара и будут выражены в физических весах, мерах длины и т. п. В статистической практике натуральные единицы измерения могут быть составными. Применяют условно–натуральные единицы измерения при суммировании количества разнородных товаров, продуктов.

Трудовые единицы измерения (человеко–дни, человеко–часы) используются для определения затрат труда на производства продукции, выполнение работы и т.д.

Абсолютные величины измеряются в стоимостных единицах – ценах. В стоимостных единицах измеряют доходы населения, валовой выпуск продукции и др.

№28.Относительные величины и их показатели.

 

Наряду с абсолютными величинами одной из важнейших форм обобщающих показателей в статистике являются относительные величины – это обобщающие показатели, выражающие меру количественных соотношений, присущих конкретным явлениям или статистическим объектам. При расчете относительной величины измеряется отношение двух взаимосвязанных величин (преимущественно абсолютных), что очень важно в статистическом анализе. Относительные величины широко используются в статистическом исследовании, так как они позволяют провести сравнения различных показателей и делают такое сравнение наглядным.

Относительные величины вычисляются как отношение двух чисел. При этом числитель называется сравниваемой величиной, а знаменатель – базой относительного сравнения. В зависимости от характера изучаемого явления и задач исследования базисная величина может принимать различные значения, что приводит к различным формам выражения относительных величин. Относительные величины измеряются:

• в коэффициентах: если база сравнения принята за 1, то относительная величина выражается целым или дробным числом, показывающим, во сколько раз одна величина больше другой или какую часть ее составляет;

• в процентах, если база сравнения принимается за 100;

• в промилле, если база сравнения принимается за 1000;

• в продецимилле, если база сравнения принимается за 10 000;

• в именованных числах (км, кг, га) и др.

В каждом конкретном случае выбор той или иной формы относительной величины определяется задачами исследования и социально-экономической сущностью, мерой которого выступает искомый относительный показатель. По своему содержанию относительные величины подразделяются на следующие виды:

• выполнения договорных обязательств;

• динамики;

• структуры;

• координации;

• интенсивности;

• сравнения.

Относительная величина договорных обязательств представляет собой отношение фактического выполнения договора к уровню, предусмотренному договором:

Эта величина отражает степень выполнения предприятием своих договорных обязательств, и может быть выражена в виде числа (целого или дробного) или в процентах. При этом необходимо, чтобы числитель и знаменатель исходного отношения соответствовали одному и тому же договорному обязательству.

Относительными величинами динамики – темпами роста – называются показатели, характеризующие изменение величины общественных явлений во времени. Относительная величина динамики показывает изменение однотипных явлений за период времени. Рассчитывается эта величина посредством сравнения каждого последующего

периода с первоначальным или предыдущим. В первом случае получаем базисные величины динамики, а во втором – цепные величины динамики. И те и другие величины выражаются либо в коэффициентах, либо в процентах. Выбору базы сравнения при расчете относительных величин динамики, как и других относительных показателей, следует уделять особое внимание, так как от этого в существенной мере зависит практическая ценность полученного результата.

Относительные величиныг структуры^ характеризуют составные части изучаемой совокупности. Относительная величина совокупности рассчитывается по формуле

Относительные величины структуры, обычно называемые удельными весами, рассчитываются делением определенной части целого на общий итог, принимаемый за 100 %. У этой величины есть одна особенность – сумма относительных величин изучаемой совокупности всегда равна 100 % или 1 (в зависимости от того, в чем она выражается). Относительные величины структуры применяются при изучении сложных явлений, распадающихся на ряд групп или частей, для характеристики удельного веса (доли) каждой группы в общем итоге.

Относительные величины координации характеризуют соотношение отдельных частей совокупности с одной из них, принятой за базу сравнения. При определении этой величины одна из частей целого берется за базу для сравнения. С помощью этой величины можно соблюдать пропорции между составляющими совокупности. Показателями координации является, например, число городских жителей, приходящихся на 100 сельских; число женщин, приходящихся на 100 мужчин, и т. п. Характеризуя соотношение между отдельными частями целого, относительные величины координации придают им наглядность и позволяют, если это возможно, контролировать соблюдение оптимальных пропорций. Так как числитель и знаменатель относительных величин координации имеют одинаковую единицу измерения, то эти величины выражаются не в именованных числах, а в процентах, промилле или кратных отношениях.

Относительными величинами интенсивности называются показатели, определяющие степень распространенности данного явления в какой-либо среде. Они рассчитываются как отношение абсолютной величины данного явления к размеру среды, в которой оно развивается. Относительные величины интенсивности находят широкое применение в практике статистики. Примером этой величины может быть отношение численности населения к площади, на которой оно проживает, фондоотдача, обеспеченность населения врачебной помощью (численность врачей на 10 000 населения), уровень производительности труда (выпуск продукции на одного работника или в единицу рабочего времени) и т. п.

Таким образом, относительные величины интенсивности характеризуют эффективность использования различного рода ресурсов (материальных, финансовых, трудовых), социальный и культурный уровень жизни населения страны, многие другие аспекты общественной жизни.

Относительные величины интенсивности вычисляются путем сопоставления разноименных абсолютных величин, находящихся в определенной связи друг с другом, и в отличие от других видов относительных величин являются обычно именованными числами и имеют размерность тех абсолютных величин, соотношение которых они выражают. Тем не менее в ряде случаев, когда полученные результаты расчетов слишком малы, их умножают для наглядности на 1000 или 10 000, получая характеристики в промилле и продецимилле.

Особый интерес представляет разновидность относительных величин интенсивности – валовой внутренний продукт на душу населения. Применяя этот показатель в различных отраслях или конкретных видах продукции, можно получать следующие относительные величины интенсивности: производство электроэнергии, топлива, машин, оборудования, услуг, товаров и т. д. на душу населения.

Относительными величинами сравнения называются относительные показатели, получающиеся в результате сравнения одноименных уровней, относящихся к различным объектам или территориям, взятым за один и тот же период или на один момент времени. Они также исчисляются в коэффициентах или процентах и показывают, во сколько раз одна сравнимая величина больше или меньше другой.

Относительные величины сравнения находят широкое применение при сравнительной оценке различных показателей работы отдельных предприятий, городов, регионов, стран. При этом, например, результаты работы конкретного предприятия и т. п. принимаются за базу сравнения и последовательно соотносятся с результатами аналогичных предприятий других отраслей, регионов, стран и т. д.

В статистическом изучении общественных явлений абсолютные и относительные величины дополняют друг друга. Если абсолютные величины характеризуют как бы статику явлений, то относительные величины позволяют изучить степень, динамику, интенсивность развития явлений. Для правильного применения и использования абсолютных и относительных величин в экономико-статистическом анализе необходимо:

• учитывать специфику явлений при выборе и расчете того или иного вида абсолютных и относительных величин (поскольку количественная сторона явлений, характеризуемая этими величинами, неразрывно связана с их качественной стороной);

• обеспечить сопоставимость сравниваемой и базисной абсолютной величины с точки зрения объема и состава представляемых ими явлений, правильности методов получения самих абсолютных величин;

• комплексно использовать в процессе анализа относительные и абсолютные величины и не отрывать их друг от друга (так как использование одних только относительных величин в отрыве от абсолютных может привести к неточным и даже ошибочным выводам).

 

№29 Понятие о средних величинах

.Виды средних и способы их вычисления.

Признаки единиц статистических совокупностей различны по своему значению, например, заработная плата рабочих одной профессии какого-либо предприятия не одинакова за один и тот же период времени, различны цены на рынке на одинаковую продукцию, урожайность сельскохозяйственных культур в хозяйствах района и т.д. Поэтому, чтобы определить значение признака, характерное для всей изучаемой совокупности единиц, рассчитывают средние величины. Средняя величина – это обобщающая характеристика множества индивидуальных значений некоторого количественного признака. Совокупность, изучаемая по количественному признаку, состоит из индивидуальных значений; на них оказывают влияние, как общие причины, так и индивидуальные условия. В среднем значении отклонения, характерные для индивидуальных значений, погашаются. Средняя, являясь функцией множества индивидуальных значений, представляет одним значением всю совокупность и отражает то общее, что присуще всем ее единицам. Средняя, рассчитываемая для совокупностей, состоящих из качественно однородных единиц, называется типической средней. Например, можно рассчитать среднемесячную заработную плату работника той или иной профессиональной группы (шахтера, врача библиотекаря). Разумеется, уровни месячной заработной платы шахтеров в силу различия их квалификации, стажа работы, отработанного за месяц времени и многих других факторов отличаются друг от друга, так и от уровня средней заработной платы. Однако в среднем уровне отражены основные факторы, которые влияют на уровень  заработной платы, и взаимно погашаются различия, которые возникают вследствие индивидуальных особенностей работника. Средняя заработная плата отражает типичный уровень оплаты труда для данного вида работников. Получению типической средней должен предшествовать анализ того, насколько данная совокупность качественно однородна. Если совокупность состоит их отдельных частей, следует разбить ее на типические группы (средняя температура по больнице). Средние величины, используемые в качестве характеристик для неоднородных совокупностей, называются системными средними. Например, средняя величина валового внутреннего продукта (ВВП) на душу населения, средняя величина потребления различных групп товаров на человека и другие подобные величины, представляющие обобщающие характеристики государства как единой экономической системы. Средняя должна вычисляться для совокупностей, состоящих из достаточно большого числа единиц. Соблюдение этого условия необходимо для того, чтобы вошел  в силу закон больших чисел, в результате действия которого случайные отклонения индивидуальных величин от общей тенденции взаимно погашаются.     Виды средних и способы их вычисления Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. Однако любая средняя величина должна вычисляться так, чтобы при замене ею каждой варианты осредняемого признака не изменился итоговый, обобщающий, или, как его принято называть, определяющий показатель, который связан с осредняемым показателем. Например, при замене фактических скоростей на отдельных отрезках пути их средней скоростью не должно измениться общее расстояние, пройденное транспортным средством за одно и тоже время; при замене фактических заработных плат отдельных работников предприятия средней заработной платой не должен измениться фонд заработной платы. Следовательно, в каждом конкретном случае в зависимости от характера имеющихся данных, существует только одно истинное среднее значение показателя, адекватное свойствам и сущности изучаемого социально-экономического явления. Наиболее часто применяются  средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая и средняя кубическая. Перечисленные средние относятся к классу степенных средних и объединяются общей формулой: , где  – среднее значение исследуемого признака; m – показатель степени средней; – текущее значение (варианта) осредняемого признака; n – число признаков. В зависимости от значения показателя степени m различают следующие виды степенных средних: при m = -1 –  средняя гармоническая ; при m =  0 – средняя геометрическая ; при m =  1 – средняя арифметическая ; при m =  2 – средняя квадратическая ; при m =  3 – средняя кубическая . При использовании одних и тех же исходных данных, чем больше показатель степени m в вышеприведенной формуле, тем больше значение средней величины: . Это свойство степенных средних возрастать с повышением показателя степени определяющей функции называется правилом мажорантности  средних. Каждая из отмеченных средних может приобретать две формы: простую и взвешенную. Простая форма средней применяется, когда средняя вычисляется по первичным (несгруппированными) данным. Взвешенная форма – при расчете средней по вторичным (сгруппированным) данным.    

№ 30.Средняя арифметическая и ее свойства

редняя арифметическая – самый распространенный вид средней величины. Когда речь идет о средней величине без указания ее вида, подразумевается именно средняя арифметическая. Она исчисляется в тех случаях, когда объем усредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности. Например, общий фонд заработной платы – это сумма заработных плат отдельных работников, общее число рабочих в промышленности – это сумма их численностей на отдельных промышленных предприятиях, общий сбор урожая – сумма урожаев с каждого гектара площади и т.д.

При исчислении средней арифметической выполняют две операции:

• суммируют индивидуальные значения признаков

• полученную сумму делят на число значений

В зависимости от характера исходных данных средняя арифметическая может быть рассчитана по формуле простой или взвешенной средней.

Если исходные данные не систематизированы, то применяется формула простой средней арифметической.

Если исходные данные сгруппированы и представлены весами (частотами), т.е. с числом единиц, имеющих одинаковые значения признака, то среднюю арифметическую исчисляют по формуле взвешенной средней.

При расчете средней арифметической взвешенной:

• необходимо умножить варианты на все ;

• сложить полученные произведения;

• сложить веса (частоты);

• сумму произведений вариант на веса разделить на сумму весов.

Обычно средняя арифметическая исчисляется по формуле взвешенной средней. Простую среднюю используют только в тех случаях, когда у каждой варианты частота равна единице или если частоты у всех вариант равны друг другу.

Принято различать три основных приема расчета средней арифметической:

• если статистические данные по индивидуальным значениям признака, полученные из наблюдения не упорядочены, то техника вычисления средней арифметической сводится к суммированию варианта и делению полученной суммы на число вариант варьирующего признака. Используется формула средней арифметической простой. В тех случаях, когда варианта повторяется и это выражено частотами, применяют формулу средней арифметической взвешенной.

• Если исходные данные представлены общей суммой значений варьирующего признака и численностью единиц совокупности то общий объем признака делится на число единиц совокупности. Такого рода данные имеются в периодической статистической отчетности.

В этом случае необходимо проверить, соответствует ли объем признака численности единиц совокупности. Ведь объем осредняемых признаков часто являются самостоятельными категориями и показателями (например, фонд заработной платы), которые подсчитываются независимо от расчета средних величин. Поэтому прежде чем исчислить среднюю, необходимо проверить выполнение вышеуказанного требования.

Более того можно привести немало примеров, когда каждое отдельное значение признака вовсе не фиксируется по тем или иным причинам. Так, иногда не подсчитывается урожайность на каждом отдельном гектаре площади, занятой той или иной культурой, но средняя для всей площади урожайность является одним из важных показателей продуктивности земледелия; никогда не подсчитывается, сколько валовой продукции произвел тот или иной рабочий.

Такие средние по способу расчета и по своему аналитическому значению мало отличаются от относительных величин интенсивности.

По-видимому, хотя выше говорили о том, что между средними и относительными величинами есть разница, но в то же время средняя – это отношение двух абсолютных величин, т.е. по сути относительная величина. Только средняя эта должна иметь отношение к любой единице совокупности. Относительная величина этим свойством не обладает.

• Среднюю арифметическую вычисляют на основе вариационных рядов. Для расчета средней в дискретных рядах варианты (значения которых известно) нужно умножить на частоту и сумму произведений разделить на сумму частот.

№31.Средняя гармоническая,квадратическая,геометрическая,хронологическая.

В статистике используются различные виды средних величин:

– средняя арифметическая;

– средняя гармоническая;

– средняя геометрическая;

– средняя хронологическая и т. д. 

При использовании средних величин важно правильно выбрать вид средней и способ ее расчета.

Самой распространенной средней, используемой в социально-экономическом анализе, является средняя арифметическая.

Средние арифметические бывают:

–простые;

–взвешенные. 

^ Средняя арифметическая простая рассчитывается по формуле

 (1)

где Х - среднее значение признака;

? - означает знак суммирования, т.е. сложения отдельных признаков;

n - число единиц совокупности.

^ Средняя арифметическая взвешенная рассчитывается по формуле

= (2)

где X - варианты;

f - частоты.

Для расчета средней арифметической необходимо иметь ряд индивидуальных значений признака (X) и частоту каждой из них (f).

Частоты f в формуле средней арифметической взвешенной называют весами, поэтому средняя арифметическая, вычисленная с учетом весов, получила название взвешенной.

Формулу (2) применяют в расчетах при условии, что известны абсолютные частоты (например, количество предприятий, численность рабочих и т.д.). 

В случаях, когда варианты носят интервальный характер, чтобы вычислить общую среднюю, необходимо найти середину, т.е. центральное значение каждого интервала.

Исчисление средних по данным интервальных рядов с закрытыми интервалами производится по формуле средней арифметической простой.

Если первый интервал дан открытым, где отсутствует нижняя граница, то условно считаем, что этот интервал равен последующему. Затем от верхней границы первого интервала вычитаем найденный интервал и таким образом находим нижнюю границу первого интервала. Затем по формуле средней арифметической простой находим среднее значение первого интервала

 (3)

Для расчета среднего значения нижнего открытого интервала, у которого отсутствует верхняя граница, поступают следующим образом: принимаем интервал не последующий (которого нет), а предыдущий. Затем к нижней границе последнего интервала прибавляют найденное значение интервала – это будет верхняя граница последнего интервала. Затем по формуле (3) находим среднее значение последнего интервала

В некоторых случаях средняя рассчитывается по другому: когда известен ряд вариант (х) и ряд произведений вариант на частоту (xf), а сама частота (f) неизвестна. В этом случае средняя рассчитывается по формуле средней гармонической взвешенной:

 (4)

где w=xf.

Выбор той или иной формулы расчета средней величины зависит от имеющейся информации.

^ Средняя хронологическая величина применяется для определения среднего уровня в моментных рядах динамики. Средний уровень ряда динамики характеризует типическую величину абсолютных уровней

Моментные – это такие ряды, где данные представлены на определенный момент времени (на определенную дату).

В моментном ряду динамики с равноотстоящими уровнями средний уровень определяется по формуле

, (5)

где у – уровни интервального ряда;

n - количество равных периодов времени.

^ Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т. е. характеризует средний коэффициент роста.

^ Средний темп роста Т рассчитывается по формуле средней геометрической цепных темпов роста, выраженных в коэффициентах. Если анализируемый период разбит на равные отрезки времени, то средний темп роста рассчитывается по формуле

  (6)

или

 (7)

где m = n-1 число процентных темпов роста.

№32.Правило мажорантности степенных средних

Правило мажорантности и свойства средней арифметической

Все формы средней, как указывалось выше, образованы от единой степенной средней и отличаются друг от друга лишь показателями степени. Правильность расчета средней величины можно проверить с помощью правила мажорантности:

То есть, правило мажорантности утверждает, что чем выше степень рассчитываемой формы средней величины, тем больше значение средней.

№33.Абсолютные показатели вариации признака:размах,дисперсия,среднее линейное и среднее квадратическое отклонения.

Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности. Исследование вариации имеет большое практическое значение и является необходимым звеном в экономическом анализе. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию.

Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей.

Абсолютные показатели вариации включают:

размах вариации 

среднее линейное отклонение 

дисперсию 

среднее квадратическое отклонение 

Размах вариации (R)

Размах вариации — это разность между максимальным и минимальным значениями признака

Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности.

Пример

Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.

Решение: размах вариации = 9 — 2 = 7 лет.

Для обобщенной характеристики различий в значениях признака вычисляют средние показатели вариации, основанные на учете отклонений от средней арифметической. За отклонение от средней принимается разность .

При этом во избежании превращения в нуль суммы отклонений вариантов признака от средней (нулевое свойство средней) приходится либо не учитывать знаки отклонения, то есть брать эту сумму по модулю , либо возводить значения отклонений в квадрат 

Среднее линейное и квадратическое отклонение

Среднее линейное отклонение  — это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней.

Среднее линейное отклонение простое:

Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет.

В нашем примере:  лет;

Ответ: 2,4 года.

Среднее линейное отклонение взвешенное применяется для сгруппированных данных:

Среднее линейное отклонение в силу его условности применяется на практике сравнительно редко (в частности, для характеристики выполнения договорных обязательств по равномерности поставки; в анализе качества продукции с учетом технологических особенностей производства).

Среднее квадратическое отклонение

Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение () равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:

Среднее квадратическое отклонение простое:

Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:

Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение:  ~ 1,25.

Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.

Дисперсия

Дисперсия - представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.

Дисперсия простая:

В нашем примере:

Дисперсия взвешенная:

Более удобно вычислять дисперсию по формуле:

которая получается из основной путем несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней.

Для несгрупиированных данных:

Для сгруппированных данных:

Вариация альтернативного признака заключается в наличии или отсутствии изучаемого свойства у единиц совокупности. Количественно вариация альтернативного признака выражается двумя значениями: наличие у единицы изучаемого свойства обозначается единицей (1), а его отсутствие — нулем (0). Долю единиц, обладающих изучаемым признаком, обозначают буквой , а долю единиц, не обладающих этим признаком — через . Учитывая, что p + q = 1 (отсюда q = 1 — p), а среднее значение альтернативного признака равно 

,

средний квадрат отклонений

Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным свойством (), на долю единиц, данным свойством не обладающих ().

Максимальное значение средний квадрат отклонения (дисперсия) принимает в случае равенства долей, т.е. когда  т.е. . Нижняя граница этого показателя равна нулю, что соответствует ситуации, при которой в совокупности отсутствует вариация. Среднее квадратическое отклонение альтернативного признака:

Так, если в изготовленной партии 3% изделий оказались нестандартными, то дисперсия доли нестандартных изделий , а среднее квадратическое отклонение  или 17,1%.

Среднее квадратическое отклонение  равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической.

№34.Основные свойства дисперсии.Соотношение среднего линейного и среднего квадратического отклонений.

№35.Относительные показатели вариации.

Относительные показатели вариации включают:

Коэффициент осцилляции 

Относительное линейное отклонение (линейный коэффициент варианции) 

Коэффициент вариации (относительное отклонение) 

Сравнение вариации нескольких совокупностей по одному и тому же признаку, а тем более по различным признакам с помощью абсолютных показателей не представляется возможным. В этих случаях для сравнительной оценки степени различия строят относительные показатели вариации. Они вычисляются как отношения абсолютных показателей вариации к средней:

Коэффициент осцилляции

Относительное линейное отклонение

Коэффициент вариации

Рассчитываются и другие относительные характеристики. Например, для оценки вариации в случае асимметрического распределения вычисляют отношение среднего линейного отклонения к медиан

,

так как благодаря свойству медианы сумма абсолютных отклонений признака от ее величины всегда меньше, чем от любой другой.

В качестве относительной меры рассеивания, оценивающей вариацию центральной части совокупности, вычисляют относительное квартильное отклонение , где  — средний квартиль полусуммы разности третьего (или верхнего) квартиля () и первого (или нижнего) квартиля ().

.

На практике чаще всего вычисляют коэффициент вариации. Нижней границей этого показателя является нуль, верхнего предела он не имеет, однако известно, что с увеличением вариации признака увеличивается и его значение. Коэффициент вариации является в известном смысле критерием однородности совокупности (в случае нормального распределения).

Рассчитаем коэффициент вариации на основе среднего квадратического отклонения для следующего примера. Расход сырья на единицу продукции составил (кг): по одной технологии  при , а по другой —  при. Непосредственное сравнение величины средних квадратических отклонений могло бы привести к неверному представлению о том, что вариация расхода сырья по первой технологии интенсивнее, чем по второй (. Относительная мера вариации ( позволяет сделать противоположный вывод

36)Мы немало говорили о самом распространенном показателе в статистике – средней величине. Однако средняя величина – понятие растяжимое, а мы пока ограничилось только средней арифметической простой и взвешенной. Главное назначение средней величины заключается в том, что она обобщает некоторый набор данных, отражает его закономерный уровень, или, как говорят ученые,центральную тенденцию. Средняя величина при некоторых условиях способна одним значением охарактеризовать сразу всю совокупность данных.

В статистике есть целый набор показателей, которые характеризуют центральную тенденцию. Выбор того или иного индикатора в основном зависит от характера данных, целей расчетов и его свойств. Например, основное свойство средней арифметической заключается в том, что сумма всех отклонений от нее равна нулю. Отсюда сумму всех уровней можно легко найти путем перемножения средней арифметической и количества значений в совокупности. Это очень удобно и не требует перечисления всех исходных значений. Теперь о характере данных.

Что подразумевается под характером данных? Прежде всего, мы говорим о количественных данных, которые выражены в числах. Это понятно. Но набор числовых данных может иметь разное так называемое распределение. Под распределением понимаются частоты отдельных значений. К примеру, в классе из 23 (двадцати трех) человек 2 (два) школьника написали контрольную работу на двойку, 5 (пять) – на тройку, 10 (десять) – на четверку и 6 (шесть) – на пятерку. Вот это есть распределение оценок. Распределение очень наглядно можно представить с помощью специального графика – гистограммы. Для данного примера получится следующая гистограмма.

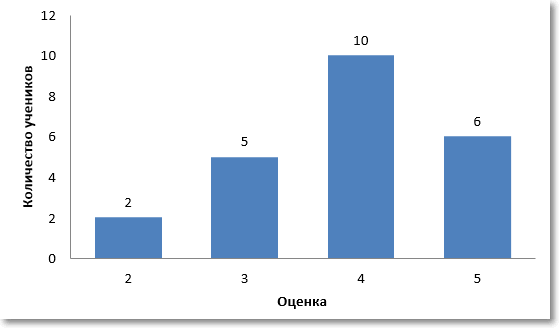
Очень наглядно, не правд ли? Правда, конечно. Лучше один раз увидеть график, чем сто раз прочитать набор чисел. Через глаза в мозг поступает 90% информации, и о визуализации данных я планирую сделать огромный специальный раздел на блоге. Следите за рекламой.

Если объем данных большой (сотня и более), а сами данные имеют случайный характер, то частоты значений во многих случаях будут распределены по т.н. нормальному закону. Этот закон, конечно, не нормативный акт, изданный правительством, а просто известная закономерность, которая наблюдается во многих явлениях и процессах и которая хорошо описана с помощью математических терминов и формул. Очень грубо суть закона нормального распределения случайных чисел заключается в том, что распределение частот отдельных значений имеет симметричный вид относительно некоторого центра, возле которого концентрируется большинство значений анализируемой совокупности, при этом частота отдаленных от центра значений резко снижается. Кажется, так.

С помощью графика-гистограммы также легко получить наглядное представление о нормальном распределении. На практике все виды графиков называют диаграммами, поэтому не будем сильно умничать. Суть одно и то же. Ниже приведена иллюстрация нормального распределения случайных чисел.

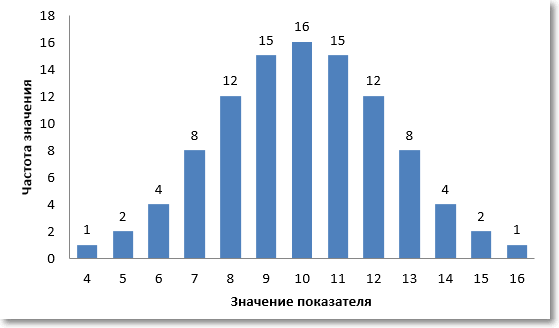
По горизонтали обозначены конкретные значения, по вертикали – их частота в соответствии с нормальным законом распределения. Колоколообразная кривая, сформированная частотами, ранжированными по возрастанию, называется кривой нормального распределения или кривой Гаусса. Это был краткий экскурс в понятие нормального распределения. Оно нам понадобится для того, чтобы понять содержимое этой статьи.

Итак, центральная тенденция. Если частоты анализируемых значений распределены по нормальному закону, то есть симметрично вокруг некоторого центра, то центральная тенденция определяется вполне однозначно – это есть тот самый центр, и математически он соответствует средней арифметической.

Как нетрудно заметить, в этом же центре находится и максимальная частота значений. То есть при нормальном распределении центральная тенденция есть не только средняя арифметическая, но и максимальная частота, которая в статистике называется модой или модальным значением.

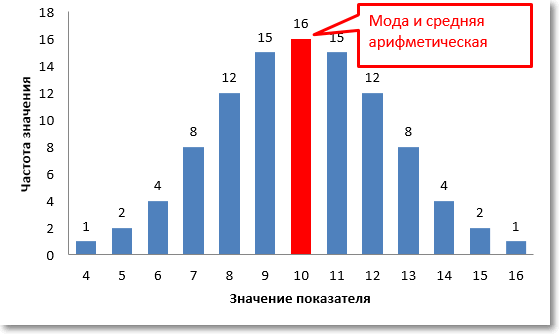
На графике оба значения центральной тенденции совпадают и равны 10 (десяти) – по горизонтальной оси, а частота соответствует красному столбцу (самому высокому). Но это только при данном, симметричном, виде распределения частот.

Как нетрудно догадаться, подобная ситуация встречается не всегда, а при малом числе данных – совсем редко. Хотя до этого обычно никому нет дела. Чаще бывает так, что частоты распределяются асимметрично. Тогда мода и среднее арифметическое не будут совпадать.

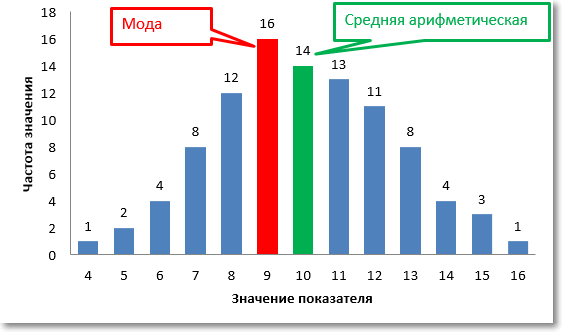
При подобном варианте распределения среднее арифметическое по-прежнему составляет 10 (десять), а вот мода уже равна 9 (девяти). Что в таком случае считать значением центральной тенденции? Ответ зависит от поставленных целей анализа. Если нас интересует уровень, сумма отклонений от которого равна нулю со всеми вытекающим отсюда свойствами и последствиями, то это средняя арифметическая. Если нужно максимально частое значение, то это мода. Выбор на совести аналитика. Действительно, почему бы наибольшую частоту не считать главной характеристикой совокупности?

Итак, зачем нужна мода? Приведу пару примеров. Экономист планово-экономического отдела обувной фабрики интересуется, какой размер обуви пользуется наибольшим спросом. Средний размер обуви, скорее всего, здесь не подойдет, тем более, что число может получится дробным. А вот мода – как раз нужный показатель. Моду в дискретном ряду не рассчитывают, а выбирают из имеющихся данных.

Другой пример. При анализе доходов населения используют усредненные показатели. Для этого обычно рассчитывают среднюю арифметическую. Мол, средняя з/п (или доход) по стране такая-то. Однако этот показатель имеет свои нюансы и может некорректно отразить динамику благосостояния населения в целом и/или его большей части. Представим, что доходы основной части населения не изменились, а вот самые богатые вдруг неожиданно стали еще богаче. Как это отразиться на средней арифметической? Очевидно, что она увеличится. И, если о динамике доходов судить только по средней арифметической, то сложится впечатление, что благосостояние населения улучшилось. На самом деле население (основная часть) не стала богаче. Рост средней арифметической произошел за счет наращивания капитала относительно немногочисленной группы населения. Вывод при использовании только средней арифметической будет не корректным. А вот если привлечь модальное значение, то оно будет отражать уровень доходов наибольшего количества людей и не будет зависеть от дохода богатых. Таким образом, усредненный доход населения приобретет несколько другой окрас. Конечно, средний арифметический доход тоже имеет право на существование, но его правильная интерпретация требует соответствующего понимания. По телевизору и других СМИ вы таких тонкостей, к сожалению, не встретите. Тамошние аналитики обычно выполняют другую функцию. Борьба за рейтинги и поддержку населением «прогрессивных» идей имеет мало общего с просвещением. Таковы «свободные» СМИ.

Моду также привлекают для анализа различных технических экспериментов. В общем, мода – достаточно известный в аналитике показатель. Знать и понимать нужно в обязательном порядке. Хотя бы для того, чтобы правильно интерпретировать среднюю арифметическую.

37) Мода   – это наиболее часто встречающееся значение варьирующего признака в вариационном ряду. Модой распределения называется такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто, т.е. один из вариантов признака повторяется чаще, чем все другие. Для дискретного ряда (ряд, в котором значение варьирующего признака представлены отдельными числовыми показателями) модой является значение варьирующего признака обладающего наибольшей частотой. Для интервального рядасначала определяется модальный интервал (т.е. содержащий моду), в случае интервального распределения с равными интервалами определяется по наибольшей частоте; с неравными интервалами – по наибольшей плотности, а определение моды требует проведения расчетов на основе следующих формул:

 

 

 

где:     - нижняя граница модального интервала;

              - величина модального интервала;

         - частота модального интервала;

       - частота интервала, предшествующего модальному;

       - частота интервала, следующего за модальным;

 

 

 

 

Медиана   - это значение варьирующего признака, приходящееся на середину ряда, расположенного в порядке возрастания или убывания числовых значений признака, т.е. величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда. Главное свойство медианы в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:

 

 

 

 

Для определения медианы в дискретном ряду при наличии частот, сначала исчисляется полусумма частот, а затем определяется какое значение варьирующего признака ей соответствует. При исчислении медианы интервального ряда сначала определяются медианы интервалов, а затем определяется какое значение варьирующего признака соответствует данной частоте. Для определения величины медианы используется формула:

 

 

где:     - нижняя граница модального интервала;

              - величина модального интервала;

       - накопленная частота интервала, предшествующего медианному;

         - частота медианного интервала;

 

Медианный интервал не обязательно совпадает с модальным.

 

 

 

Моду и медиану в интервальном ряду распределения можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который в данном случае является модальным. Затем правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс.

Медиана рассчитывается по кумуляте (рис. 2). Для её определения из точки на шкале накопленных частот (частностей), соответствующей 50%, проводится прямая, параллельная оси абсцисс, до пересечения с кумулятой. Затем из точки пересечения указанной прямой с кумулятой опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения является медианой.

 

 38) Предоставляют важную информацию о структуре вариационного ряда к-л признака. Вместе с медианой они делят вариационный ряд на 4 равные части. Квартилей две, их обозначают символами Q, верхняя и нижняя квартиль. 25% значений меньше, чем нижняя квартиль, 75% значений меньше, чем верхняя квартиль.

Для расчёта квартили надо поделить вариационный ряд медианой на две равные части, а затем в каждой из них найти медиану. К примеру, если выборка состоит из 6 элементов, тогда за начальную квартиль выборки принимается второй элемент, а за нижнюю квартиль пятый элемент.

Дециль характеризует распределение величин совокупности, при котором девять значений дециля делят её на десять равных частей. Любая из этих десяти частей составляет 1/10 всей совокупности. Так, первый дециль отделяет 10 % наименьших величин, лежащих ниже дециля от 90 % наибольших величин, лежащих выше дециля.

Так же, как в случае моды и медианы, у интервального вариационного ряда распределения каждый дециль (и квартиль) принадлежит определённому интервалу и имеет вполне определённое значение^[1].

Перцентиль[править | править исходный текст]

-ой перценти́лью называют квантиль уровня  . При этом обычно рассматривают перцентили для целых  , хотя данное требование не обязательно. Соответственно, медиана является 50-й перцентилью, а первый и третий квартиль — 25-й и 75-й перцентилями.

В целом, понятия квантиль и перцентиль взаимозаменяемы, так же как и шкалы исчисления вероятностей — абсолютная и процентная.

Перцентили также называются процентилями или центилями.

39) Понятие о статистических рядах динамики .

Ряды динамики – статистические данные , отображающие развитие во времени изучаемого явления . Их также называют динамическими рядами , временными рядами .

В каждом ряду динамики имеется два основных элемента :

1) показатель времени t ;

2) соответствующие им уровни развития изучаемого явления y;

В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты), либо отдельные периоды (годы , кварталы, месяцы, сутки).

Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления . Они могут выражаться абсолютными , относительными или средними величинами .

Ряды динамики различаются по следующим признакам :

1) По времени . В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам . В соответствии с этим ряды динамики подразделяются на моментные и интервальные .

Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени . Примером моментного ряда динамики является следующая информация о списочной численности работников магазина в 1991 году (таб. 1):

Таблица 1[]

Списочная численность работников магазина в 1991 году

Дата	1.01.91	1.04.91	1.07.91	1.10.91	1.01.92
Число работников , чел.	192	190	195	198	200

Особенностью моментного ряда динамики является то , что в его уровни могут входить одни и те же единицы изучаемой совокупности . Хотя и в моментном ряду есть интервалы – промежутки между соседними в ряду датами , -- величина того или иного конкретного уровня не зависит от продолжительности периода между двумя датами . Так , основная часть персонала магазина , составляющая списочную численность на 1.01.1991 , продолжающая работать в течение данного года , отображена в уровнях последующих периодов . Поэтому при суммировании уровней моментного ряда может возникнуть повторный счет .

Посредством моментных рядов динамики в торговле изучаются товарные запасы , состояние кадров , количество оборудования и других показателей , отображающих состояние изучаемых явлений на отдельные даты (моменты) времени .

Интервальные ряды динамики отражают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени .

Примером интервального ряда могут служить данные о розничном товарообороте магазина в 1987 – 1991 гг. (таб. 2):

Таблица 2[]

Объем розничного товарооборота магазина в 1987 - 1991 гг.

Год	1987	1988	1989	1990	1991
Объем розничного товарооборота , тыс. р.	885.7	932.6	980.1	1028.7	1088.4

Каждый уровень интервального ряда уже представляет собой сумму уровней за более короткие промежутки времени . При этом единица совокупности , входящая в состав одного уровня , не входит в состав других уровней .

Особенностью интервального ряда динамики является то , что каждый его уровень складывается из данных за более короткие интервалы (субпериоды) времени . Например , суммируя товарооборот за первые три месяца года , получают его объем за I квартал , а суммируя товарооборот за четыре квартала , получают его величину за год , и т. д. При прочих равных условиях уровень интервального ряда тем больше , чем больше длина интервала , к которому этот уровень относится .

Свойство суммирования уровней за последовательные интервалы времени позволяет получить ряды динамики более укрупненных периодов .

Посредством интервальных рядов динамики в торговле изучают изменения во времени поступления и реализации товаров , суммы издержек обращения и других показателей , отображающих итоги функционирования изучаемого явления за отдельные периоды .

Статистическое отображение изучаемого явления во времени может быть представлено рядами динамики с нарастающими итогами. Их применение обусловлено потребностями отображения результатов развития изучаемых показателей не только за данный отчетный период , но и с учетом предшествующих периодов . При составлении таких рядов производится последовательное суммирование смежных уровней . Этим достигается суммарное обобщение результата развития изучаемого показателя с начала отчетного периода (года , месяца , квартала и т. д.) .