14. Уравнение движения подвижного состава

Для вывода уравнения движения рассмотрим разгон автомобиля на подъеме (рис. 3.21).

Спроецируем все силы, действующие на автомобиль, на поверхность дороги:

Rx2 – Rx1 – Рп – Рв – Ри=0. (3.19)

Подставим в формулу (3.19) касательные реакции дороги Rx1 и Rx1, объединим члены с коэффициентом сопротивления качению f и члены с ускорением j и, принимая во внимание соотношения f(Rz1 + Rz2) = Pк и Jk1 + Jk2 = Jk, a также коэффициент учета вращающихся масс, получим уравнение движения автомобиля в общем виде:

Рт – Рк – Рп – Рв – Ри=0,

ИЛИ

Рт – Рд – Рв – Ри=0. (3.20)

Уравнение движения автомобиля выражает связь между движущими силами и силами сопротивления движению. Оно позволяет определить режим движения автомобиля в любой момент.

Так, например, при установившемся (равномерном) движении

Рт – Рд – Рв =0,

Из уравнения (3.20) следует, что безостановочное движение автомобиля возможно только при условии

Рт ≥ Рд + Рв .

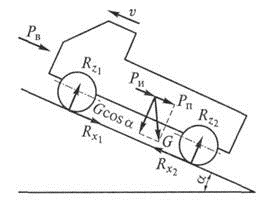
Рис. 3.21. Схема сил, действующих на автомобиль на подъеме

Данное неравенство связывает конструктивные параметры автомобиля с эксплуатационными факторами, обусловливающими сопротивление движению. Однако оно не гарантирует отсутствия буксования ведущих колес. Безостановочное движение автомобиля без буксования ведущих колес возможно лишь при соблюдении условия

Рсц ≥ Рт ≥ Рд + Рв .

Условие равномерного движения при отсутствии буксования ведущих колес записывается в виде

Рсц ≥ Рт = Рд + Рв .

15. Коэффициент учета вращающихся масс

Все эксплуатационные свойства автомобиля взаимосвязаны между собой, но в зависимости от его предназначения и условии эксплуатации на первый план выходят те эксплуатационные свойства, которые являются главными.

Что касается того или иного эксплуатационного свойства автомобиля, то оно является комплексным показателем, зависящим от целого ряда факторов. Параметры, по которым оценивают то или иное эксплуатационное свойство автомобиля также обладают различной значимостью.

Установление значимости параметра и оценка влияния его на то или иное эксплуатационное свойство само по себе является весьма актуальной проблемой.

В теории автомобиля оперируют понятием коэффициента учета вращающихся масс автомобиля при решении уравнении его неравномерного движения, торможения и др.

Коэффициент учета вращающихся масс автомобиля является также комплексным, т.к. касается всего автомобиля. Поэтому для установления значимости всех параметров входящих в выражение для определения этого коэффициента, а также оценки их влияния на то или иное эксплуатационное свойство автомобиля необходимо определить единичные коэффициенты учета вращающихся масс автомобиля.

В этом ряду одним из немаловажных является возможность оценки коэффициента учета вращающихся масс колес автомобиля, т.к. именно через колеса осуществляется контакт автомобиля с дорогой.

Составляя уравнение неравномерного движения переднего ведомого колеса автомобиля получаем выражение

(1)

где бвр1 = 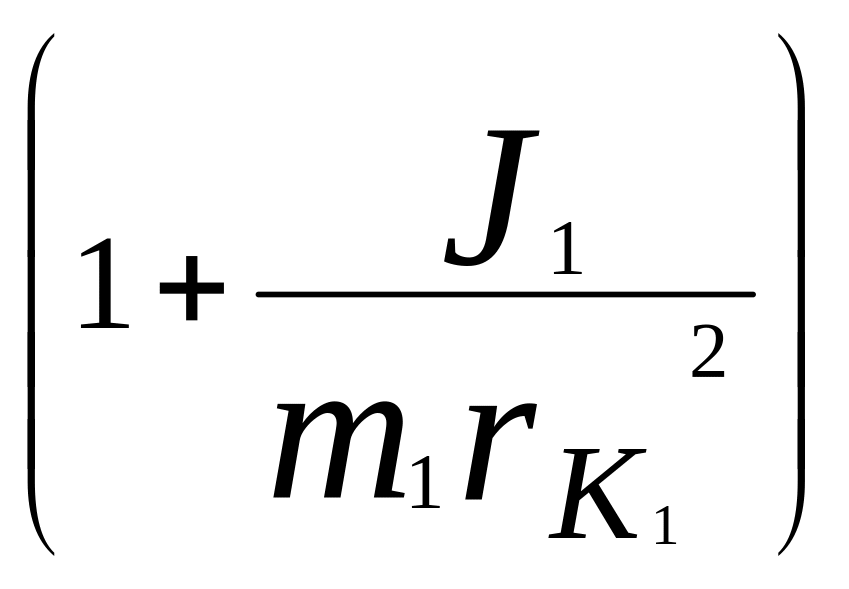- коэффициент учета вращающихся масс переднего ведомого колеса автомобиля;

J1, m1 и r k1 - соответственно момент инерции, масса и радиус переднего ведомого колеса; Xтол –толкающая сила переднего ведомого колеса; Z1 – нормальная реакция дороги на переднее колесо; ƒ1 –коэффициент сопротивления качению переднего ведомого колеса; j1-ускорение переднего ведомого колеса автомобиля.

Перепишем уравнение (1), с учетом движения на подъем, в виде

Xтол = Pg1 + Fu1 , (2)

где Pg1 - сила дорожного сопротивления для данного колеса;

Fu1 - приведенная сила инерции переднего ведомого колеса автомобиля.

Полученное уравнение (2) можно назвать уравнением силового баланса переднего ведомого колеса автомобиля, которое решается графическим методом, аналогично решению силового баланса всего автомобиля.

Аналогично составляя уравнение неравномерного движения заднего ведущего колеса автомобиля получим

X_M = P_T – Z₂f₂ – m₂ j₂ , (3)

где б вр2 = - коэффициент учета вращающихся масс заднего ведущего колеса автомобиля; J2 , m2 и rk2 - соответственно момент инерции, масса и радиус заднего ведущего колеса; Z2 – нормальная реакция дороги на задниее колесо; f2 - коэффициент сопротивления качению заднего ведущего колеса; XM – горизонтальная реакция автомобиля на ведущее колесо; j2 – ускорение заднего ведущего колеса автомобиля.

Перепишем уравнение (3), с учетом движения на подъем в виде

Р_T = Pg₂ + Fu₂ + X_M , (4)

где РT – тяговая сила, приложенная к ведущему колесу автомобиля; Pg2 - сила дорожного сопротивления для данного колеса; Fu2 –приведенная сила инерции заднего ведущего колеса автомобиля.

Полученное уравнение (4) можно назвать уравнением силового баланса заднего ведущего колеса автомобиля, которое также решается графическим методом, аналогично решению силового баланса всего автомобиля.

Рассмотрение движения колес автомобиля как в отдельности, так и совместно позволит оценить влияние как единичных, так и комплексных показателей автомобиля на его эксплуатационные свойства.