Замечание. Геометрические характеристики сечений, координаты центров тяжести сечений относительно начальных и центральных осей целесообразно оформить в виде таблицы (см. Пример расчета),

6. Проводится контроль правильности определения координат центров тяжести сечения и его элементов. Для этого вычисляется статический момент сечения относительно центральных осей, которые при правильном расчете должны равняться нулю:

;  . (2.5) Замечание. Все расчеты проводятся с ограниченной точностью. Инженерные расчеты, обычно, проводят с учетом 3 – 4 значащих цифр. Оставлять большее число значащих цифр нецелесообразно, так как исходные данные (исходные размеры и значения геометрических характеристик) не обеспечивают большую точность и поэтому результаты с большим числом значащих цифр нельзя считать более достоверными. Точность результата оценивают, обычно, относя невязку (разность между приближенным и точным значением) к точному или приближенному значению. Однако, если результатом вычислений должен быть ноль, такой подход невозможен. В этом случае отдельно подсчитывают положительные   и отрицательные   слагаемые и абсолютное значение невязки и относят невязку к сумме положительных (или отрицательных) слагаемых: . (2.6)  Погрешность инженерных расчетов обычно не должна превышать 3%. 7. Определяют геометрические характеристики сечения – осевые, полярный и центробежный моменты инерции сечения относительно центральных осей ; ;  ; . (2.7) Заметим, что площадь, осевые и полярный моменты инерции являются строго положительными характеристиками сечений. Однако, для сечений с отверстиями бывает удобным считать отверстия элементами сечений с отрицательными характеристиками. Пр имер. Определить координаты центра тяжести и осевые моменты инерции сечения в виде круга радиусом r =3а с круговым отверстием радиуса r₀ = a, касающимся центра круга (рис. 2.2). Принимаем за 1-й элемент сплошной круг радиусом r =3а, за второй элемент отверстие радиуса r₀ = a. Начальные оси проводим через центр тяжести 1-го элемента.  Тогда имеем: ;  ; ;  ;  . Так как ось р является осью симметрии сечения, так же как и осями симметрии элементов сечения, то эта ось является центральной осью у и  . Следовательно, для определения положения центра тяжести сечения требуется определить только координату р_с 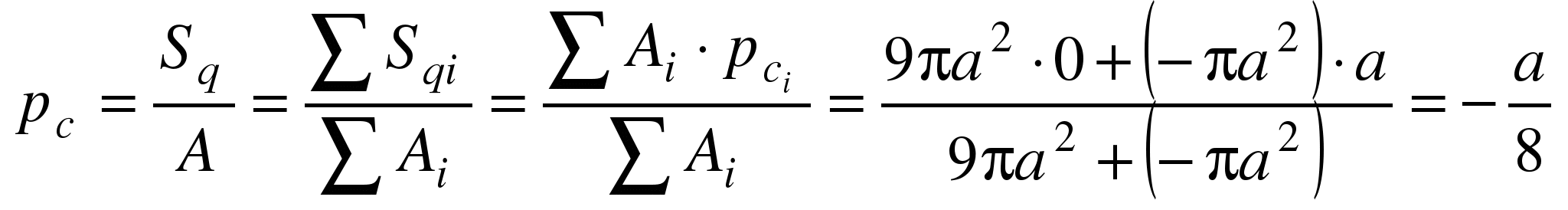. Координаты центров тяжести элементов относительно центральных осей: ;  ;  ;  .  Осевые моменты инерции круга относительно собственных центральных осей определяются по формуле  .  . Следовательно, имеем: ;  . Определяем осевые моменты инерции сечения ; . Так как сечение имеет ось симметрии, то центробежный момент инерции сечения равен нулю и оси у, z являются главными.  8. Определяем положение главных осей сечения Главными осями сечения являются центральные оси, относительно которых осевые моменты инерции достигают максимального и минимального значений и называются главными моментами инерции сечения. Центробежный момент инерции относительно главных осей равен нулю. Положение главных осей определяется поворотом центральных осей на угол ₀, определяемый по формуле . (2.8) При этом берется главное значение арктангенса, т.е.  -90 < 2₀ < ; -4590 < ₀ < .45 Главные оси показываются на схеме (чертеже) сечения. 9. Вычисление главных моментов инерции. Осевые моменты инерции при повороте осей на угол  вычисляются по формулам: ; ; . (2.9) Значения главных моментов инерции получаем при подстановке в формулы осевых моментов (2.9) угла ₀, определенного по формуле (2.8). Подстановка значение угла₀ в формулу (2.9) для центробежного момента инерции должна дать нулевое значение, что позволяет провести проверку правильности определения угла поворота главных осей. Определяя значения главных моментов инерции по формулам (2.9) мы одновременно определяем относительно какой оси осевой момент инерции будет иметь максимальное и относительно какой минимальное значение.  Значения главных моментов инерции может быть определено без использования значения угла ₀. В этом случае используются формулы: 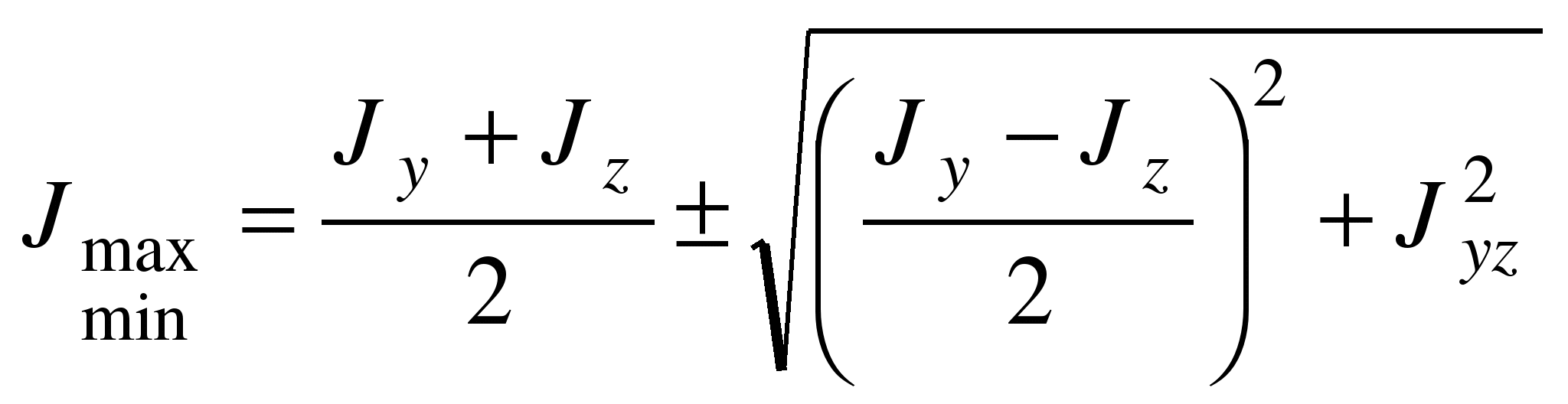. (2.10) Формула (2.10) не дает ответа относительно какой из двух взаимно перпендикулярных осей главный момент инерции будет иметь максимальное, а относительно какой минимальное значение. Однако можно показать, что из двух главных осей, ось, относительно которой главное значение будет максимальным, будет ближе к центральной оси (у или z) с наибольшим значение осевого момента (J_y или J_z соответственно). Так как при повороте осей полярный момент не изменяется то правильность их определения проверяется по формуле  . (2.11) Отметим, что знание значений главных моментов инерции и положение главных осей поперечных сечений стержня необходимо при проведении расчетов напряженно деформированного состояния стержней на изгиб, кручение и различные виды сложных видов сопротивления стержней. 

17. Напряжения в наклонных сечениях при плоском напряженном состоянии Напряженное состояние называется плоским, если одно из главных напряжений равно нулю. Определим нормальные и касательные напряжения в наклонном сечении (см. рис. 1.9). Их можно представить как сумму нормальных и касательных напряжений, возникающих отдельно от   и  . , где   и   — нормальные напряжения в наклонной площадке, возникающие соответственно от   и  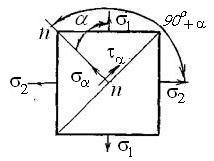. Рисунок 1.9 Значение   можно определить по формуле (1.1), так как угол между напряжением и нормалью n-n составляет  , а   — по формуле (1.3), так как угол  , но в формулу вместо   нужно подставить  :  (1.5) Аналогично для касательных напряжений: Значение   находится по формуле (1.2),  — по формуле (1.4)  с заменой   и  . ;  (1.6) Из формулы (1.5) следует, что наибольшие касательные напряжения будут при  ;  ;  .  (1.7) Наибольшие касательные напряжения возникают в площадках под углом   и равны половине разницы главных напряжений. Преобразуем формулу (1.5). Учитывая, что  , а  , получим   (1.8) Формулы (1.6) и (1.8) удобно исследовать с помощью круга Мора. Для этого преобразуем эти формулы, возведем в квадрат и сложим  ; . Получим следующее уравнение Это уравнение изображается окружностью, центр которой имеет координаты  и  , а радиус  . По этим данным строится окружность (на рис.1.10 для определенности принято, что  ). Очевидно,  ОА =  ; ОВ =  ; ОС =  ; ВС = СА =  . Чтобы найти по чертежу величины   и   для наклонной площадки, заданной углом  , достаточно через точку В, соответствующую главному напряжению  , провести прямую BD под углом   к оси  . В пересечении с окружностью получится точка D, координаты которой изображаются отрезками ОЕ и ЕD. По чертежу легко находим, что  ОЕ = ОС + СЕ =   +  ; ЕD =  . Отрезок ОD изображает полное косое напряжение  . Меняя угол   и наблюдая за перемещением точки D по окружности, можно отметить следующие характерные особенности данного напряженного состояния. Подчеркнем, что рассматриваются только такие наклонные площадки, которые перпендикулярны к третьей главной площадке. 1. Главное напряжение   является наибольшим возможным для данной задачи; оно соответствует площадкам, характеризуемым углом  , т. е. параллельным 1-й главной площадке. 2. Главное напряжение   является наименьшим возможным для данного семейства площадок: оно соответствует площадкам, параллельным 2-й главной площадке. 3. Наибольшее по абсолютной величине касательное напряжение численно равно полуразности главных напряжений   и  : . Эти напряжения изображаются точками Т и Т₁ круговой диаграммы. Соответствующие площадки составляют углы   с 1-й и 2-й главными площадками. 4. Напряжения на взаимно перпендикулярных площадках изображаются двумя точками D и D₁ диаграммы, расположенными по концам одного диаметра. Отсюда следует, что  . Формула выражает приведенный выше закон взаимности (парности) касательных напряжений. 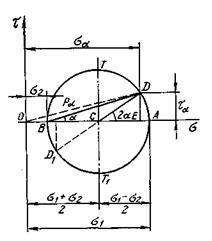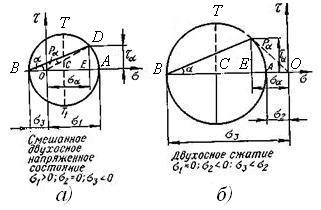Рисунок 1.10 Рисунок 1.11

Необходимо обратить внимание на тот факт, что слова «наибольшее» и «наименьшее» в пп. 1 и 2 данных выводов следует понимать  в алгебраическом, а не в арифметическом смысле. Здесь разобран случай двустороннего растяжения, когда  . Нетрудно убедиться, что в случае двустороннего сжатия (рис. 1.11 б) или в случае смешанного двухосного напряженного состояния (рис.1.11 а) аналитический вид формул остается без изменения.

18. Изгибом называется вид нагружения бруса, при котором к нему прикладывается момент, лежащий в плоскости проходящей через продольную ось. В поперечных сечениях бруса возникают изгибающие моменты. При изгибе возникают деформация, при которой происходит искривление оси прямого бруса или изменение кривизны кривого бруса.   

Брус, работающий при изгибе, называется балкой. Конструкция, состоящая из нескольких изгибаемых стержней, соединенных между собой чаще всего под углом 90, называется рамой.

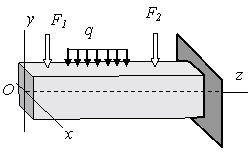
Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.6.1).

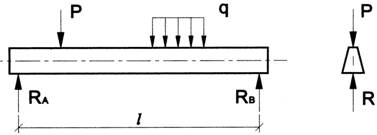
Изгибающий момент и поперечная сила

 

Плоским изгибом называется такой вид деформации стержня, при котором все внешние нагрузки, включая опорные реакции, лежат в одной из главных плоскостей стержня (yOz или xOz на рис. 6.1) и вызывают искривление оси стержня в этой плоскости. Изгибаемый стержень называется балкой.

В поперечном сечении балки могут возникать два внутренних усилия – изгибающий момент   (или  ) и поперечная сила   (или  ). Если поперечная сила отсутствует, то изгиб называется чистым, а при наличии поперечной силы изгиб называется поперечным. В дальнейшем будем рассматривать балки с поперечными сечениями, симметричными относительно оси y, и нагруженными силами в плоскости yOz.

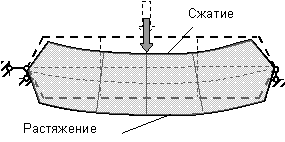
При изгибе продольная ось балки искривляется, поперечные сечения, оставаясь плоскими, поворачиваются, продольные волокна либо растягиваются, либо сжимаются (рис. 6.2).

 

Рис. 6.1. Изгиб стержня  в плоскости yOz	Рис. 6.2. Деформированное  положение балки

 

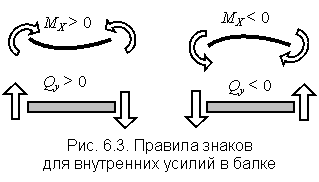
Для внутренних усилий приняты следующие правила знаков. 

Изгибающий момент считается положительным, если растянуты нижние и сжаты верхние волокна. Поперечная сила считается положительной, если стремится повернуть выделенную часть балки по ходу часовой стрелки (рис. 6.3). Между изгибающим моментом  , поперечной силой   и интенсивностью распределенной нагрузки   существуют дифференциальные зависимости   ;   ;   .

График, показывающий изменение изгибающего момента вдоль оси балки, называется эпюрой изгибающих моментов (Эп.М_х). График, показывающий изменение поперечной силы вдоль оси балки, называется эпюрой поперечных сил (Эп.Q_y). Для построения эпюр находят опорные реакции балки, потом балку разделяют на участки, на каждом из которых получают методом сечений уравнения   и  , а затем строят графики полученных функций. Ординаты эпюры   откладывают со стороны растянутых волокон балки (положительные – вниз от оси, отрицательные – вверх от оси). Положительные ординаты эпюры   откладывают вверх от оси, отрицательные – вниз от оси графика.

19 Дифференциальные зависимости при изгибе:

; ; ; .

Определение перемещений способом фиктивной нагрузки. Сопоставляя уравнения:

и имеем аналогию,  определение прогибов можно свести к определению моментов от некоторой фиктивной (условной) нагрузки в фиктивной балке: . Момент от фиктивной нагрузки М_ф после деления на EJ равен прогибу "y" в заданной балке от заданной нагрузки. Учитывая, что и , получаем, что угол поворота в заданной балке численно равен фиктивной поперечной силе в фиктивной балке. , . При этом должна быть полная аналогия в граничных условиях двух балок. Каждой заданной балке соответствует своя фиктивная балка.

Закрепление фиктивных балок выбирается из того условия, чтобы на концах балки и на опорах имелось полное соответствие между "y" и "" в заданной балке и М_ф и Q_ф в фиктивной балке. Если эпюры моментов как в действительной, так и в фиктивной балках строить со стороны растянутого волокна (т.е. положительный момент откладывать вниз), то линии прогибов в заданной балке совпадает с эпюрой моментов в фиктивной балке.

Статически неопределимые балки.

Статически неопределимыми называются системы, реакции в которых не могут быть определены из уравнений равновесия твердого тела. В таких системах больше связей, чем это необходимо для равновесия. Степень статической неопределимости балки (не имеющей промежуточных шарниров – неразрезные балки) равна избыточному (лишнему) числу внешних связей (более трех).

Р аскрытие статической неопределимости с помощью дифф-ного урав-ния изогнутой оси балки. Записываем дифф-ное урав-ние куда входит в качестве неизвестной реакция R_B и дважды его интегрируем: EJ = R_Вx – ; EJ = R_В – + С;

EJy = R_В – + Сх + D. Используем условия закрепления балки: х=0, y=0, =0; x=L, y=0. Подставляем их в два последних уравнения, находи постоянные интегрирования С и D и неизвестную реакцию R_B. Далее из урав-ний статики: H_A=0; R_A – qL + R_B=0; R_BL – + M_A=0; находятся R_A и M_A.
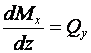
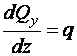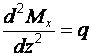