14.Геометрические характеристики плоских сечений

Площадь: , dF — элементарная площадка.

С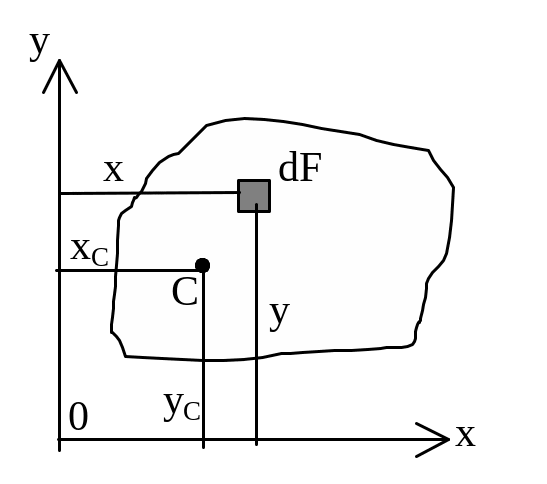 татический момент элемента площади dF относительно оси 0x — произведение элемента площади на расстояние "y" от оси 0x: dS_x = ydF

Просуммировав (проинтегрировав) такие произведения по всей площади фигуры, получаем статические моменты относительно осей y и X: ; [см3, м3, т.Д.].

Координаты центра тяжести: . Статические моменты относительно центральных осей (осей, проходящих через центр тяжести сечения) равны нулю. При вычислении статических моментов сложной фигуры ее разбивают на простые части, с известными площадями F_i и координатами центров тяжести x_i, y_i.Статический момент площади всей фигуры = сумме статических моментов каждой ее части: .

Координаты центра тяжести сложной фигуры: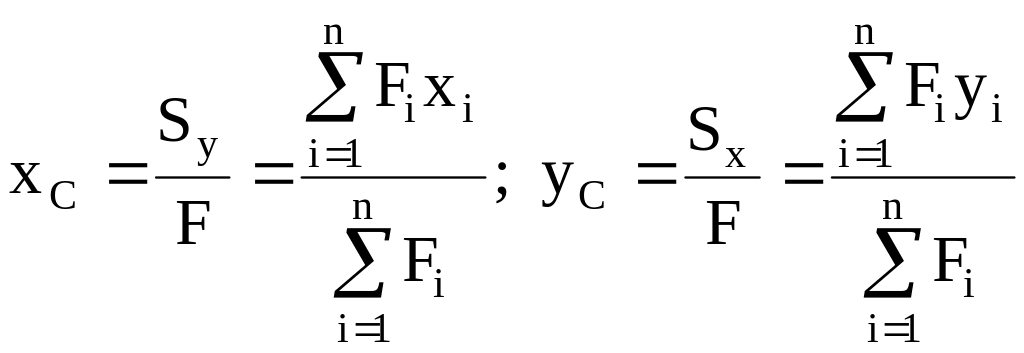

Моменты инерции плоских сечений.

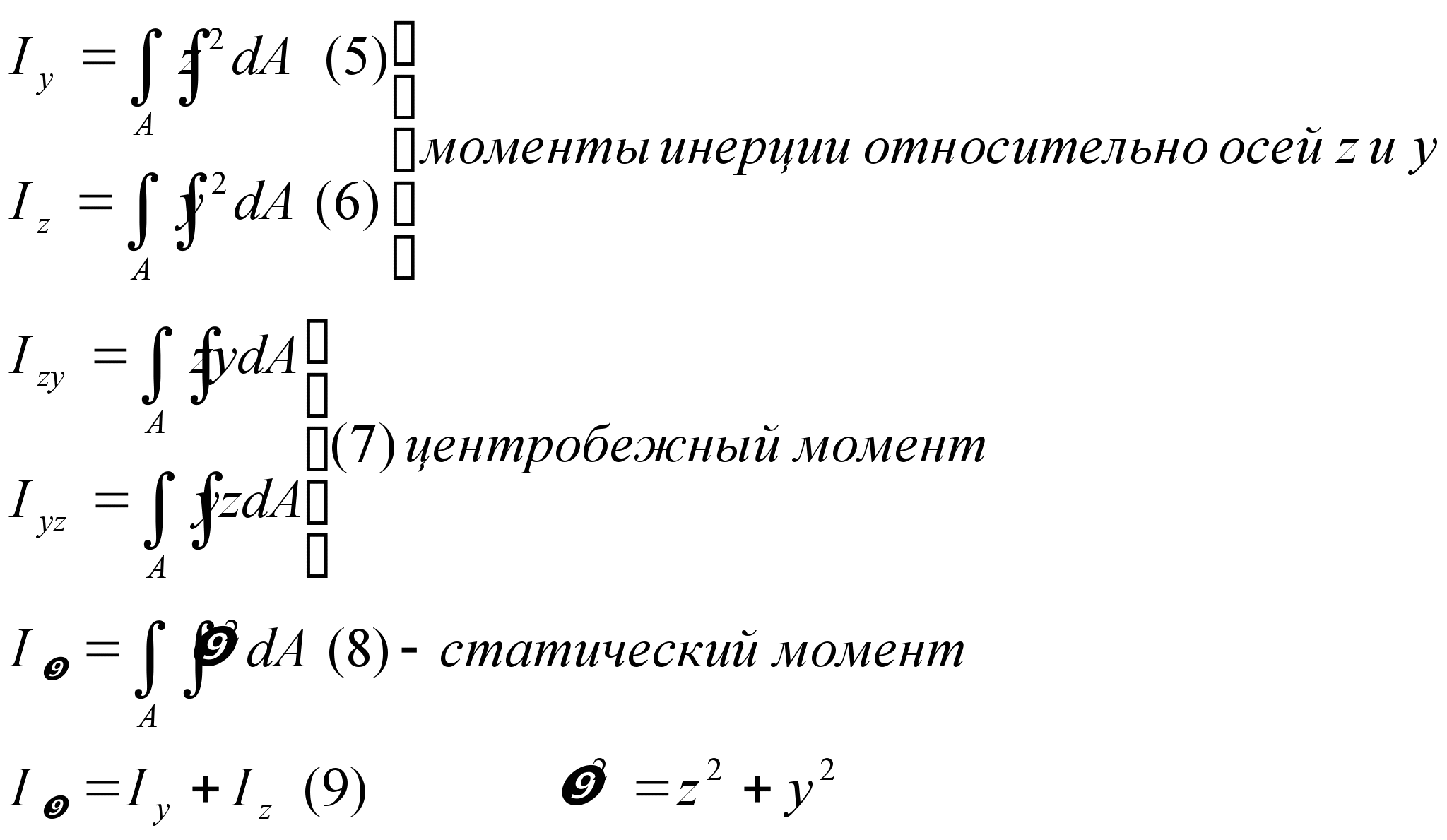
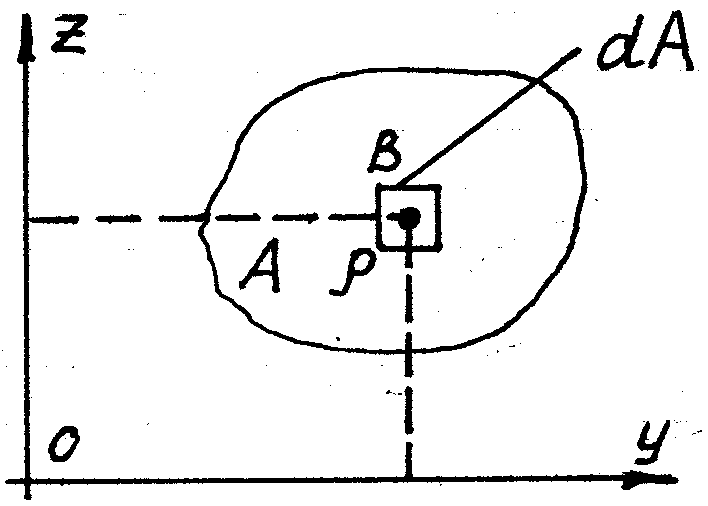
  Если одна из осей будет являться осью симметрии, то момент будет равен нулю.

Свойства аддиативности моментов инерции.

 

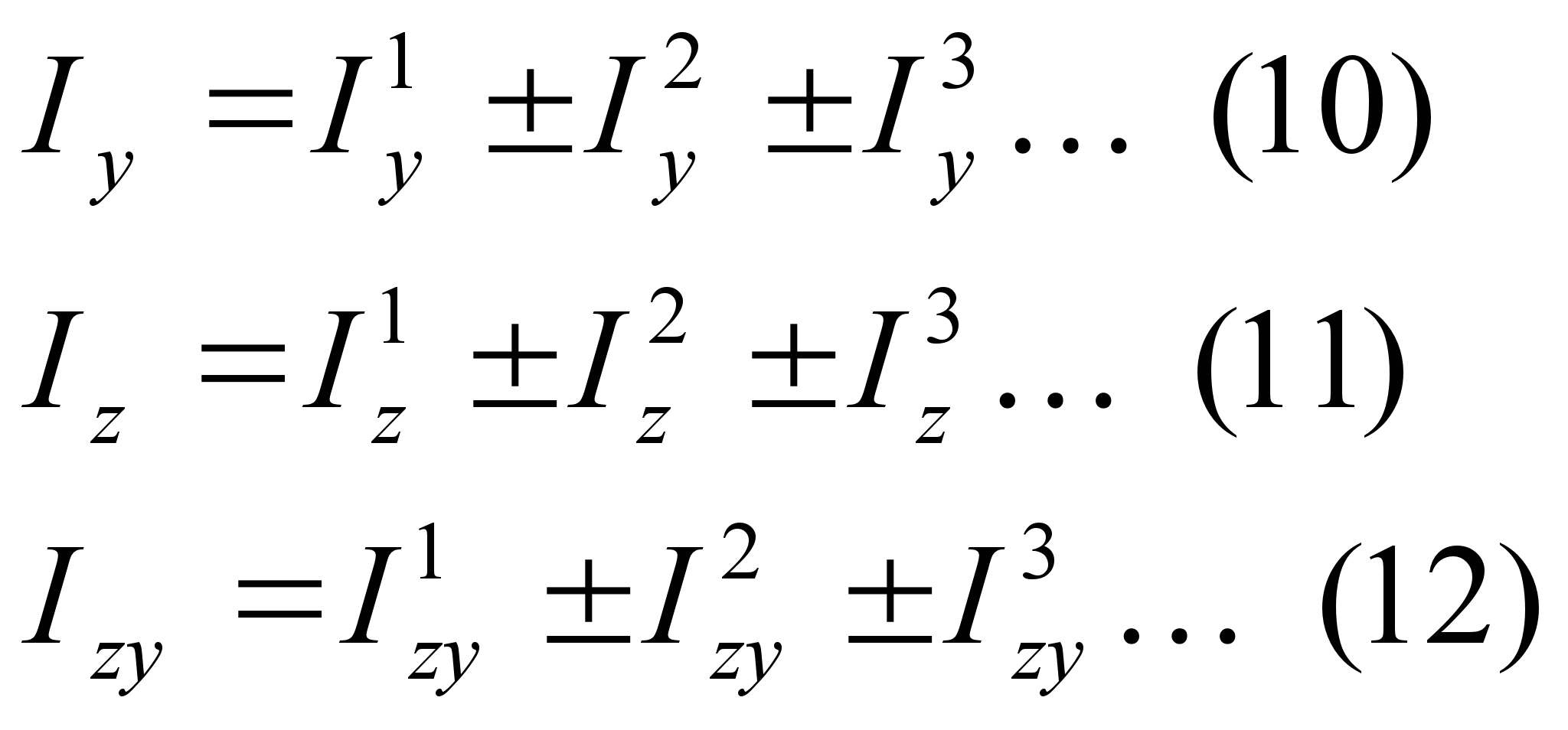
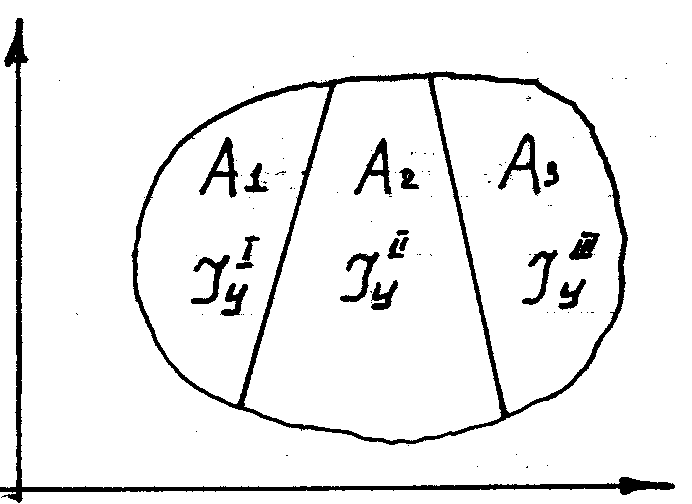
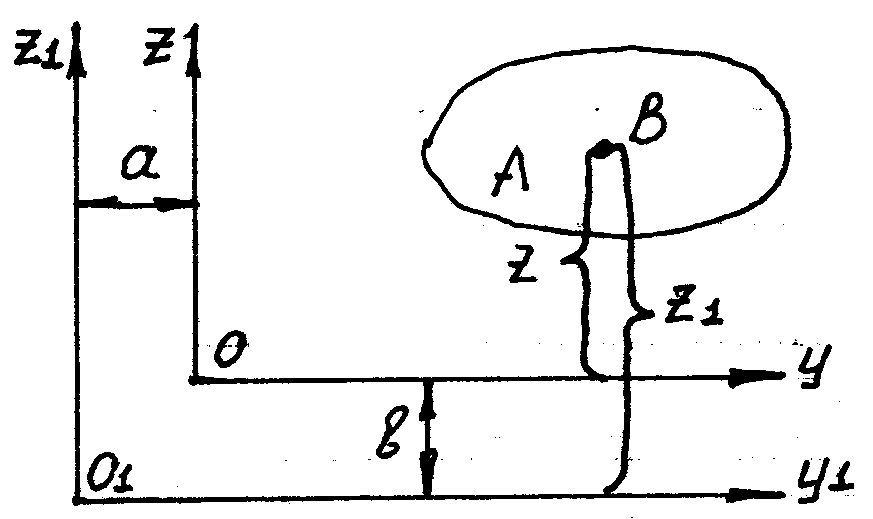
Изменение моментов инерции при параллельном переносе осей координат.

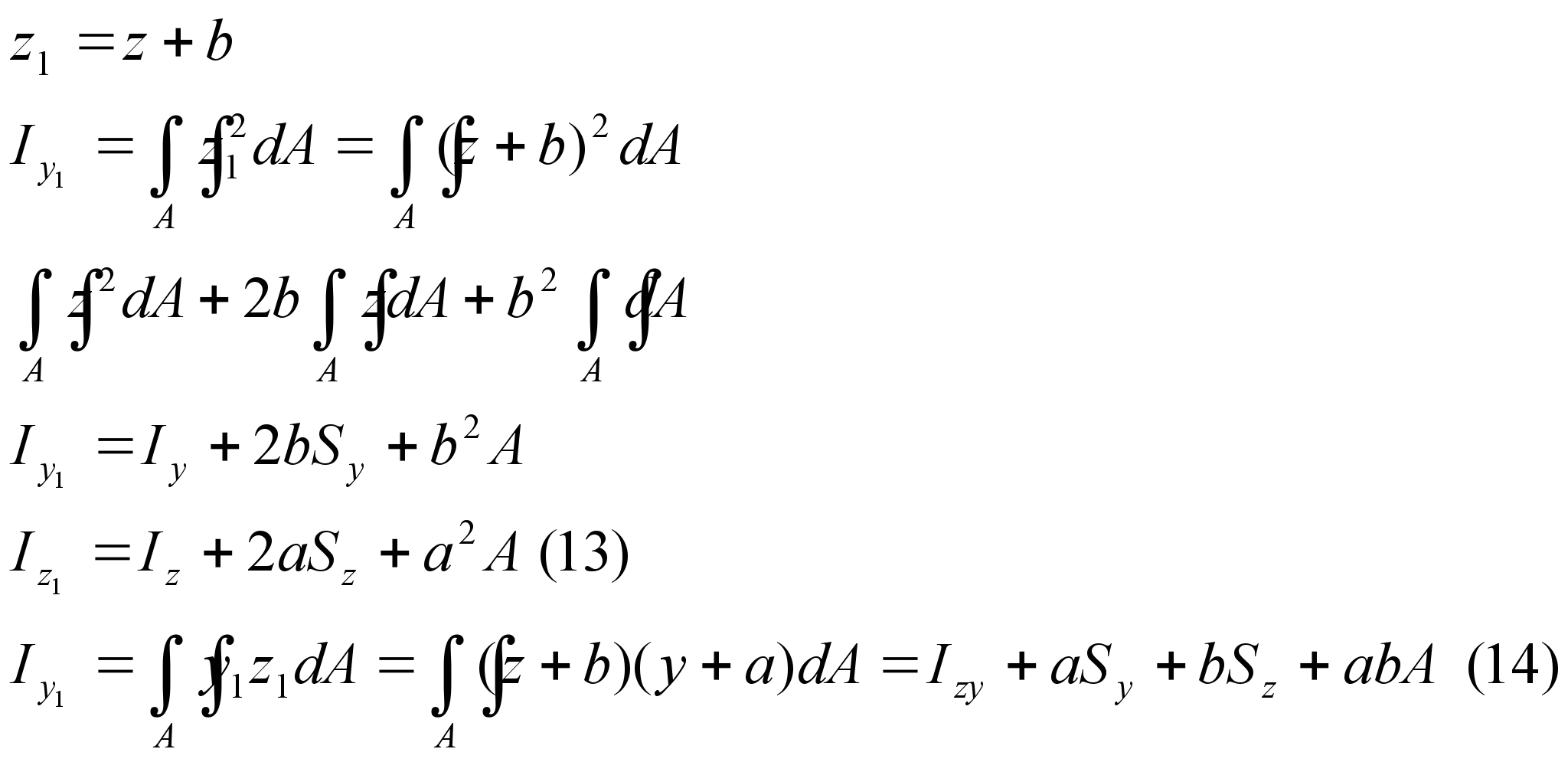Если оси являются центральными, то оси моментов будут иметь вид: 

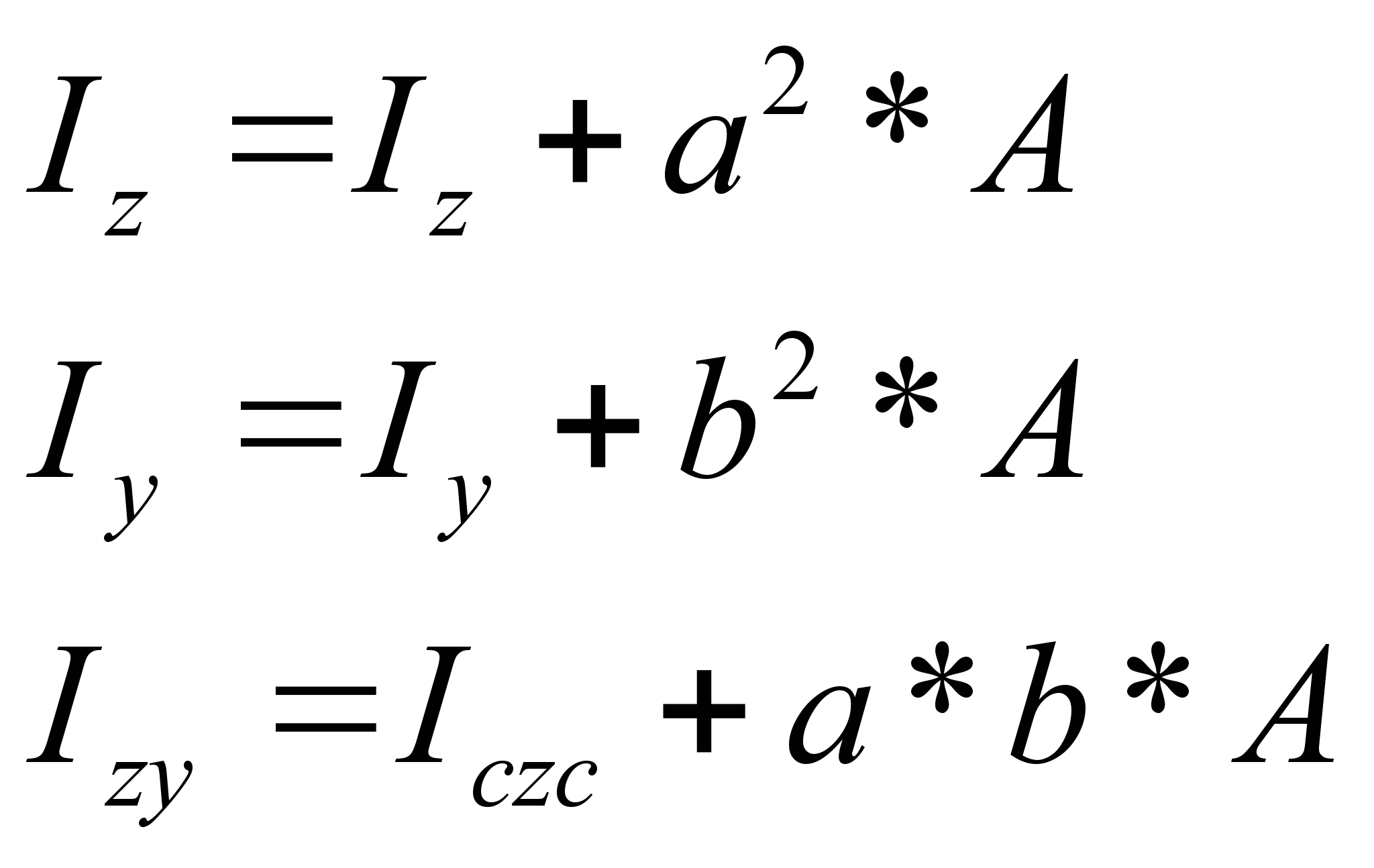
15. Зависимость между моментами инерции при повороте осей:

J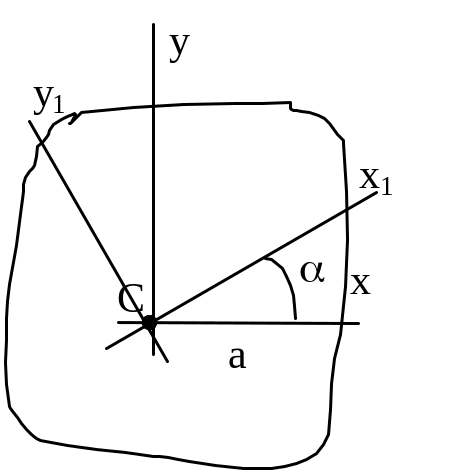 _x1=J_xcos² + J_ysin² — J_xysin2; J_y1=J_ycos² + J_xsin² + J_xysin2;

J_x1y1= (J_x — J_y)sin2 + J_xycos2 ;

Угол >0, если переход от старой системы координат к новой происходит против час.стр. J_y1 + J_x1= J_y + J_x

Экстремальные (максимальное и минимальное) значения моментов инерции называются главными моментами инерции. Оси, относительно которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси инерции взаимно перпендикулярны. Центробежные моменты инерции относительно главных осей = 0, т.е. главные оси инерции — оси, относительно которых центробежный момент инерции = 0. Если одна из осей совпадает или обе совпадают с осью симметрии, то они главные. Угол, определяющий положение главных осей: , если ₀>0  оси поворачиваются против час.стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей:

J_max + J_min= J_x + J_y. Центробежный момент инерции относительно главных центральных осей инерции равен 0. Если известны главные моменты инерции, то формулы перехода к повернутым осям:

J_x1=J_maxcos² + J_minsin²; J_y1=J_maxcos² + J_minsin²; J_x1y1= (J_max — J_min)sin2;

Конечной целью вычисления геометрических характеристик сечения является определение главных центральных моментов инерции и положения главных центральных осей инерции. Р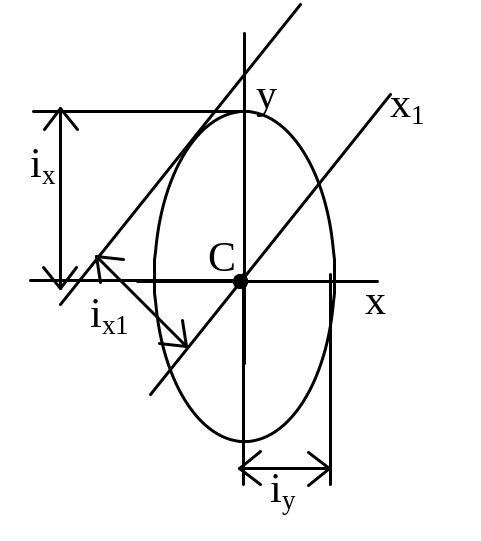 адиус инерции — ; J_x=Fi_x², J_y=Fi_y².

Если J_x и J_y главные моменты инерции, то i_x и i_y — главные радиусы инерции. Эллипс, построенный на главных радиусах инерции как на полуосях, называется эллипсом инерции. При помощи эллипса инерции можно графически найти радиус инерции i_x1 для любой оси х₁. Для этого надо провести касательную к эллипсу, параллельную оси х₁, и измерить расстояние от этой оси до касательной. Зная радиус инерции, можно найти момент инерции сечения относительно оси х₁: . Для сечений, имеющих более двух осей симметрии (например: круг, квадрат, кольцо и др.) осевые моменты инерции относительно всех центральных осей равны между собой, J_xy=0, эллипс инерции обращается в круг инерции.

16. «ОПРЕДЕЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК СОСТАВНОГО СЕЧЕНИЯ БРУСА»

РЕШЕНИЕ

1 С учетом сортамента прокатной стали (табл.П.2 ... П.5) вычерчиваем в масштабе составное сечение бруса

2. Находим геометрические характеристики сечений отдельных элементов относительно собственных центральных осей х,-у,.

3. Выбираем произвольные оси х - у и вычисляем координаты

центров тяжести элементов в этих осях:

4. Определяем координаты центра тяжести С сечения в осях х-у

5. Вычисляем координаты центров тяжести С, элементов в центральных осях x_c- y_c составного сечения

6. Используя формулы (2.8) и (2.9), находим осевые и центробежный моменты инерции составного сечения относительно центральных осей хс –ус

7.Находим положение главных центральных осей инерции х0 - у0 составного сечения 8.Вычисляем главные центральные моменты инерции составного сечения бруса

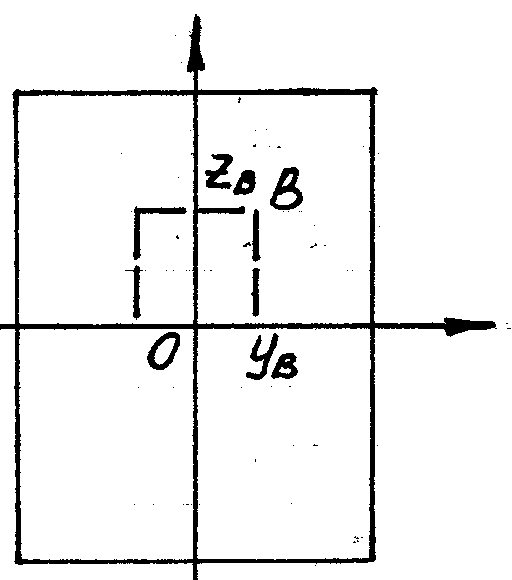
9. Находим наиболее удаленные от осей хо-уо точки составного сечения.От оси х0 наиболее удалена точка А, от оси у0 - точка В (рис.). Вычисляем их координаты в центральных осях хс-ус:

10. Определяем расстояния от главных центральных осей X0 уо до наиболее удаленных точек А иВ;

11. Находим осевые моменты сопротивления составного сечения бруса

12. При расчетах на прочность в условиях сложного сопротивления бруса, расчетах колонн на устойчивость используются главные радиусы инерции сечения

13. Определяем величины главных моментов инерции Jxo Jyo положение главных центральных осей .x0, уо графоаналитическим способом с помощью круга инерции О. Мора (обратная задача)

2.1. Определение геометрических характеристик сечений Расчет геометрических характеристик сечения проводят в следующем порядке:

1. Заданное сечение вычерчивается в определенном масштабе и разбивается на элементы, элементы нумеруются, номера элементов указываются на чертеже.

2. Задаются начальными осями р, q. Начальные оси могут задаваться произвольно. Однако, для упрощения вычислений удобно, если начальные оси проходят через центр тяжести одного или нескольких элементов сечения, на которые разбито заданное сечение. Все начальные размеры, необходимые для вычисления геометрических характеристик элементов и определения координат центров тяжестей элементов указываются на чертеже. Для прокатных профилей на чертеже сечения указываются необходимые для расчета размеры, взятые из таблиц проката.

3. Определяют координаты центров тяжести элементов сечения относительно начальных осе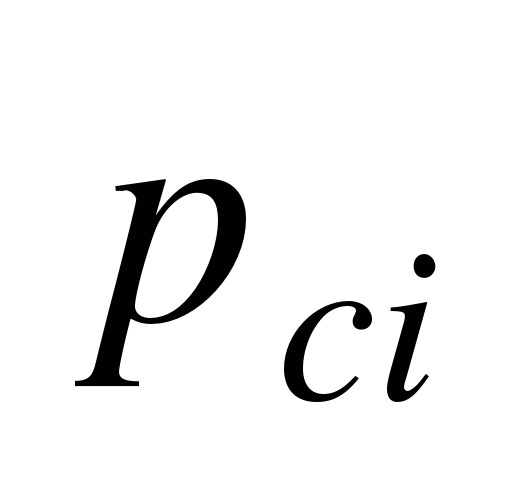й   и   и геометрические характеристики сечений относительно собственных осей элементов А_i,  ,  ,  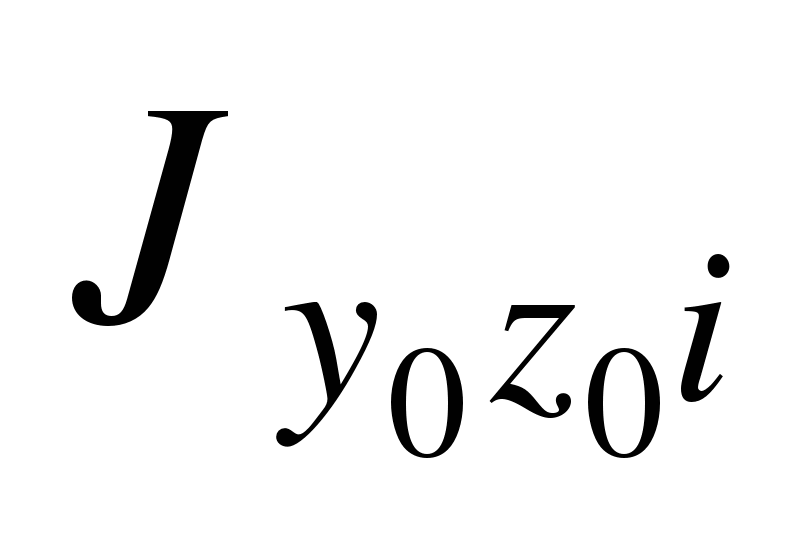. Собственные оси элементов – оси, параллельные начальным осям р, q, проходящие через центры тяжестей элементов сечения. 

Замечание. Необходимо проявлять внимательность при определении координат центров тяжестей элементов сечения и их геометрических характеристик, так как ошибки, допущенные на этом этапе не имеют алгоритма проверки и приводят к ошибочным результатам при дальнейших вычислениях. 

4. Определяют координаты центра тяжести всего сечения по формулам:

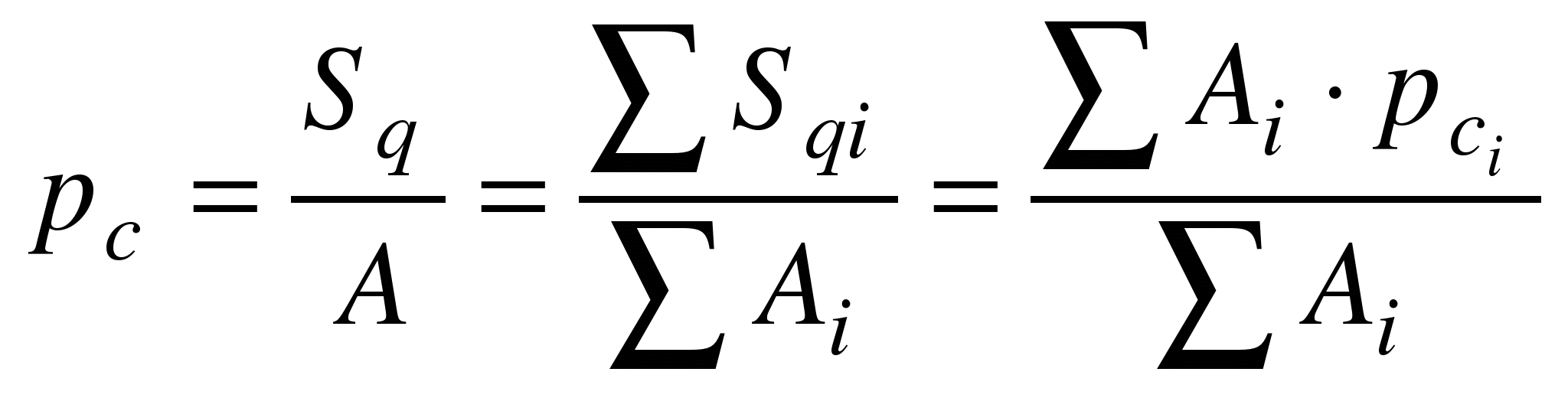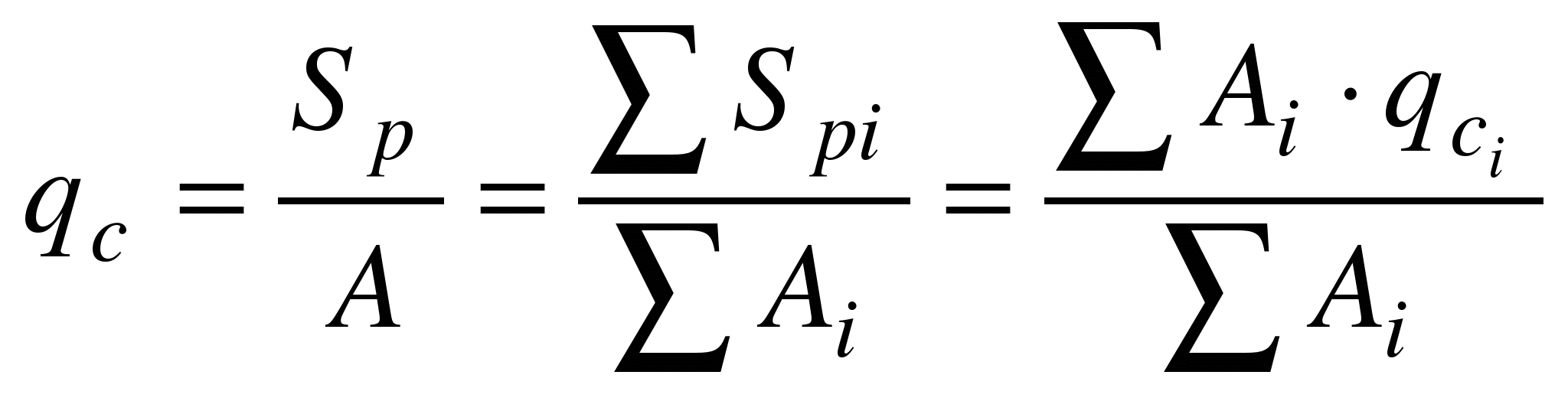;  . (2.3)  Центральные оси х, у (оси проходящие через центр тяжести всего сечения), параллельные начальным осям показываются на чертеже.  5.  Определяют координаты центров тяжести элементов сечения относительно центральных осей сечения: ;  . (2.4)