9. Напряженные состояния

Напряженное состояние в точке тела – совокупность напряжений, действующих по бесчисленному множеству площадок, которые можно провести через данную точку.

Главные площадки – площадки, на которых касательные напряжения равны нулю.

Главные напряжения – напряжения, действующие на главных площадках.

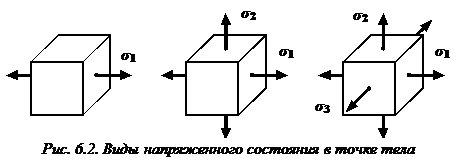
Виды напряженного состояния в точке:

а) линейное (одноосное) напряженное состояние – когда два главных напряжения равны нулю (одноосное растяжение или сжатие);

б) плоское напряженное состояние – когда только одно из главных напряжений равно нулю;

в) объёмное напряженное состояние – когда все три главных напряжения отличны от нуля.

Закон парности касательных напряжений: на двух взаимно перпендикулярных площадках касательные напряжения равны по абсолютной величине.

10.

Главные напряжения и главные площадки

Главные Напряжения И Главные Площадки Сопромат

Главные площадки – это площадки, проходящие через исследуемую точку, на которых Касательные напряжения отсутствуют.

Главные напряжения – это возникающие на главных площадках нормальные напряжения

В общем случае нагружения (при объемном напряженном состоянии) среди множества площадок, проходящих через некоторую точку тела, всегда можно найти три взаимно перпендикулярные главные площадки. В окрестности любой точки деформированного твердого тела всегда можно выделить элементарный параллелепипед, ориентированный в пространстве таким образом, что по его граням будут возникать только нормальные (главные) напряжения (см. рис. 6.2).

Главные напряжения обозначаются  . Индексы расставляются после вычисления главных напряжений. Должно выполняться неравенство:

– наибольшее, а  – наименьшее нормальное напряжение в исследуемой точке тела.

В частном случае нагружения может получиться так, что все три главных напряжения в исследуемой точке тела равны между собой. Тогда любая площадка, проведенная через эту точку, является главной площадкой.

По значениям главных напряжений дается оценка прочности материала в исследуемой точке деформированного твердого тела.

При плоском напряженном состоянии на грани элементарного параллелепипеда с нормалью х полностью отсутствует не только касательное, но и нормальное напряжение. Площадка тоже является главной площадкой, главное напряжение на которой равно нулю.

Пусть мы нашли для случая плоского напряженного состояния, что экстремальные напряжения в исследуемой точке тела равны  МПа, а  МПа. Индексы главных напряжений:  МПа,  МПа,  МПа.

Если получилось  МПа, а  МПа, то тогда  МПа,  МПа,  МПа.

11. Обобщенный закон Гука. Деформация при плоском и объемном напряжении состояния.

Обобщенный закон Гука:

Рассматривается элементарный объем вокруг точки тела при исследовании прочности в данной точке необходимо знать не только сигма 1, 2, 3 – главные напряжения, но и деформацию в этой точке. Изменение формы тела всегда связано с перемещением этих точек тела.

Это правило привело к тому, что нужно рассматривать деформацию элементарного объема по осям.

Деформации по осям, аналитическое выражение:

эбсоленx = сигма1/E – ню *(сигма2/E) –ню *(сигма3/E)

эбсоленZ = сигма2/E – ню *(сигма1/Е) – ню *(сигма3/Е)

эбсоленy = сигма3/Е – ню * (сигма1/Е) – ню *(сигма2/Е)

Исследования этого выражения приводит к зависимости объемной деформации и главных напряжений.

Аналитическое выражение для всех видов напряженного состояния.