35. Критическое напряжение. Пределы применимости формулы эйлера

При осевом нагружении стержня в его поперечных сечениях возникают нормальные напряжения сжатия, которые возрастают по мере увеличения нагрузки. Нормальные напряжения, соответствующие критической силе, называются критическими:  , или после подстановки значения критической силы из формулы,  .

В последнюю формулу входят две геометрические характеристики площади сечения стержня: минимальный момент инерции   и площадь A. Частное от деления   представляет собой величину, имеющую единицу площади м², см², мм². Поэтому линейную величину   называют минимальным радиусом инерции сечения.

Таким образом,   и последняя формула принимает вид   или  .

Безразмерная величина   называется гибкостью стержня. Она характеризует сопротивляемость стержня потере устойчивости; с увеличением гибкости уменьшается сопротивляемость стержня потере устойчивости. Заметим, что гибкость   стержня не зависит от материала стержня, а определяется его длиной, формой и размерами сечения.

Определяя значение критической силы, Эйлер исходил из рассмотрения упругой линии изогнутого стержня, поэтому формула   справедлива только в пределах применимости закона Гука, инача говоря, до тех пор, пока критическое напряжение не превышает предела пропорциональности материала стержня, т. е. при условии  . Отсюда  .

Стоящая в правой части неравенства постоянная для данного материала безразмерная величина называется предельной гибкостью:  .

Таким образом, применимость формулы Эйлера определяется условием  .

Формула Эйлера применима только в тех случаях, когда гибкость стержня больше или равна предельной гибкости того материала, из которого он изготовлен.

Рисунок 1

Как правило, многие конструкции имеют стержни с гибкостью меньше предельной. Разработку современных методов расчета на усталость таких стержней начал Ф.С.Ясинский, который предложил приближенные формулы для определения критических напряжений за пределом пропорциональности, проанализировав предварительно обширный экспериментальный материал и построив графические зависимости между и для многих материалов. 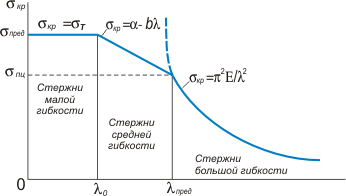График зависимости от для стержней из пластичного материала (низкоуглеродистой стали) показан на рисунке 1.

В результате исследований подобных графиков стержни условно делятся на три группы. Стержни большой гибкости ( ), для которых критические напряжения определяются по формуле Эйлера. Стержни средней гибкости ( ), для которых критические напряжения определяются по формуле Ясинского  , где коэффициенты а и b имеют для каждого материала определенное значение, найденное экспериментально. Некоторые значения этих коэффициентов, а также гибкостей   и  , в интервале между которыми применима для данного материала формула Ясинского, приведены в таблице.

Материал	a	b
	МПа
Сталь Ст2	264	0,70	60	105
Сталь Ст3	310	1,14	60	100
Сталь 20, Ст4	328	1,15	60	96
Сталь 45	449	1,67	52	85
Дюралюмин Д16Т	406	1,83	30	53
Соста, ель	29,3	0,194	-	70

Стержни малой гибкости ( ), для которых   соответствует  , т.е.   для пластичных материалов и   для хрупких материалов. Такие стержни рассчитывают не на устойчивость, а на прочность, как при простом сжатии.