31.Косой изгиб

Косым изгибом называется вид нагружения, при котором плоскость действия изгибающего момента не проходит ни через одну из главных осей сечения.

Напряжения и перемещения при косом изгибе найдем, используя принцип независимости действия сил. Косой изгиб рассматривается при этом как одновременный изгиб в 2-х плоскостях zx и zy. Для этого изгибающий момент М_изг раскладывается на составляющие моменты осей х и у.

М_х=М_изгsin a, М_у=М_изг cos a

Нормальные напряжения в любой точке поперечного сечения могут быть вычислены как алгебраическая сумма напряжений, возникающих от моментов M_x и M_y:

Сигма= М_изг((у/J_x)sin a + (x/J_y)cos a)

a - угол отклонения плоскости действия M от вертикали.

Если в каждой точке сечения отложить по нормали вектор сигма, то концы векторов, как и при простом изгибе образуют плоскость. Уравнение нейтральной линии в сечении найдем, полагая сигма=0:

У=-х(J_x/J_y) ctg a

При косом изгибе нейтральная линия не перпендикулярна к плоскости изгибающего момента.

32. Ядро сечения

        в сопротивлении материалов, область вокруг центра тяжести поперечного сечения стержня, ограниченная замкнутым контуром и обладающая тем свойством, что продольная сила, приложенная к любой её точке, вызывает в сечении напряжения одного знака ( Форма и размеры Я. с. определяются формой и размерами поперечного сечения стержня. Определение Я. с. особенно важно при расчёте стержней из материала, обладающего различной прочностью при растяжении и сжатии.

Внецентренное растяжение-сжатие

        стержня (в сопротивлении материалов), деформация, возникающая при действии на стержень двух равных и противоположно направленных продольных сил, параллельных оси стержня; один из видов сложного сопротивления (см. Сложное сопротивление). В. р.-с. характеризуется сложением деформаций от изгиба и от продольных сил. При В. р.-с. в точках поперечного сечения с текущими координатами у и z, взятыми относительно главных центральных осей (рис.), нормальные напряжения определяются по формуле:

         

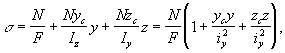
         в которой F — площадь поперечного сечения, I_y и I_z — моменты инерции сечения, i_y и i_z — радиусы инерции сечения, у_с и z_c — координаты точки приложения продольной силы N. Нормальные напряжения линейно зависят от координат и достигают максимальных значений в точках поперечного сечения, наиболее удалённых от нейтральной линии, положение которой определяется отрезками а_у и a_z, отсекаемыми на координатных осях:

         

         Если продольная сила приложена в границах ядра сечения (см. Ядро сечения), то нейтральная линия либо лежит за пределами сечения, либо касается контура сечения, при этом эпюра нормальных напряжений становится однозначной. Случаи В. р.-с. часто встречаются при расчётах фундаментов, арок, рам и других конструкций.

         Л. В. Касабьян.

        

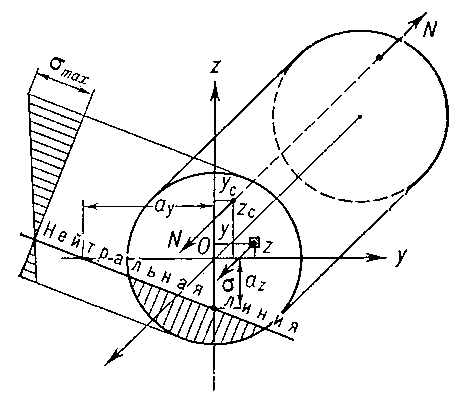
        Внецентренное растяжение-сжатие стержня.

33. Кручение круглых валов

Кручением называется такой вид нагружения (деформации), при котором в поперечных сечениях бруса возникает только один внутренний силовой фактор – крутящий момент T(рис 5.1). Этот вид нагружения возникает при приложении к брусу пар сил, плоскости действия которых перпендикулярны его оси. Такие брусья принято называть валами.

Внешние пары, приложенные к валу, будем называть скручивающими моментами. Они могут быть сосредоточенными М₁, М₂, …, М_n или распределенными m по длине вала l. Крутящий момент является равнодействующим моментом напряжений, возникающих в каком-либо  сечении вала относительно его продольной оси.