4.1. Дифференциальное уравнение изогнутой оси балки и его интегрирование.

При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией, а поступательные перемещения сечений, равные перемещениям y=y(x) их центров тяжести сечений – прогибами балки.

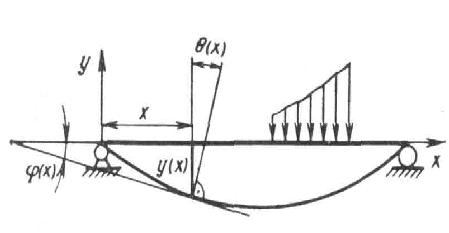
Рис. 8.22.

Между прогибами y(x) и углами поворота сечений θ(x) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сеченияθ равен углу φ наклона касательной к упругой линии (θ и φ - углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y^/=tgθ. Следовательно, tgθ=tgφ=y^/.

В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h, а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ=y^/.

Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M_z и жесткости EI_z (см. уравнение (8.8)):

.

(8.26)

В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,

.

(8.27)

Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M_z и y^// были приняты независимо друг от друга, получаем

.

(8.28)

Это равенство называется дифференциальным уравнением упругой линии. При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ=0.1 рад (y^/)²=0.01) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки

.

(8.29)

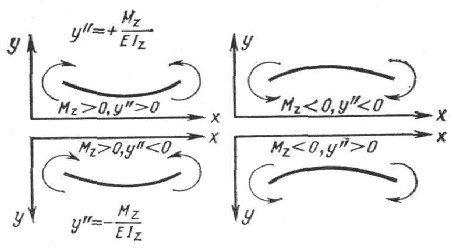
Выбор знака в правой части (8.29) определяется направлением координатной оси y, так как от этого направления зависит знак второй производной y^//. Если ось направлена вверх, то, как видно из рис. 8.23, знаки y^// и M_z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y^// и M_z противоположны, и это заставляет выбрать в правой части знак минус.

Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M_z содержит одну из главных осей инерции сечения.

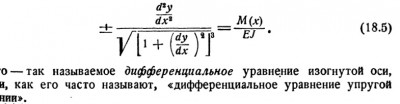
25. Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки(универсального уравнения упругой линии балки)

Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

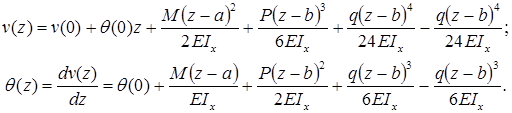
a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

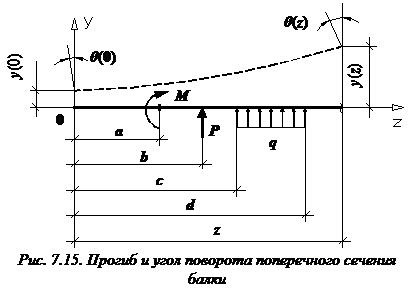
В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

Прогиб  и угол поворота  балки в начале координат (начальные параметры) определяются из условий закрепления балки.

Искривленная ось балки может описываться уравнением в дифференциальной форме , которое называется уравнением упругой линии балки и имеет общий вид:

± EJ (d²y/dx²) = M или ± EJ y″= M

Где Е – модуль упругости первого рода ,

Y - перемещение сечения балки,

J_z = bh³/12 - экваториальный момент инерции сечения балки относительно оси z.

М – изгибающий момент в сечении.

y' = dy/ dx = tg θ

где θ - угол поворота сечения балки при нагружении изгибающей нагрузкой .

Ввиду малости прогиба по сравнению с длинновыми размерами балки можно принять tg θ = θ

Уравнение прогибов сечений : Для первого участка :

EJY = - F(L-a)x₁³/6L + Fa(L-a)(2L-a)/6L;

Для второго участка

EJY = - F(L-a)x₂³/6L +F(x₂-a)³/6+ Fa(L-a)(2L-a)/6L;

Полученные зависимости позволяют определить прогибы и на консольном участке балки.

Преимущество аналитического метода- высокая точность расчетов ,а недостаток – сложность и громоздкость.

Граничные условия могут быть статическими, кинематическими и смешанными.

Статические ГУ имеют вид

 

                                  (2.20)

 

где l, m, n – направляющие косинусы;   – проекции внеш­них сил.

Если заданы компоненты смещений, то такие ГУ называют кинематическими. Если заданы одновременно компоненты перемещений и напряжений, то условия называют смешанными.
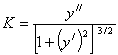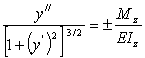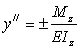