- •Основные положения
- •1. Содержание расчетно-пояснительной записки и ее оформление
- •1.1. Общие требования
- •1.2. Задание к курсовой работе
- •Для полученной расчетной схемы выполнить:
- •2 Методические указания
- •2.1.Трехфазные цепи
- •2.2 Матричные методы расчета линейных цепей
- •2.1. Обобщённое и аналитическое представления схем
- •2.2. Основные матричные уравнения электрических цепей
- •2.3. Метод симметричных составляющих
- •2.3.1. Симметричные составляющие трехфазной системы величин
- •2.3.2. Некоторые свойства трехфазных цепей в отношении симметричных составляющих токов и напряжений
- •2.4 Фильтры симметричных составляющих
- •2.4.1 Фильтры напряжения нулевой последовательности (фннп)
- •2.4.2 Фильтры тока нулевой последовательности (фтнп)
- •4.3 Фильтр напряжения обратной последовательности (фноп)
- •4.4 Фильтры тока обратной последовательности (фтоп)
- •2.5. Анализ цепей с несинусоидальными периодическими источниками
- •2.5.1 Общие положения
- •2.5.2 Особенности работы трехфазных систем, вызываемые гармониками, кратными трем.
- •2.6.Анализ переходных процессов в линейных цепях
- •2.6.1 Возникновение переходных процессов. Понятие о коммутации
- •2.6.2 Законы коммутации
- •2.6.3 Классический метод расчета переходного процесса.
- •2.6.4 Операторный метод
- •2.6.5 Метод переменных состояния
- •2.6.5.1 . Общие понятия и определения
- •2.6.5.2 Формирование уравнения в матричной форме по методу наложения
- •2.6.6 Расчёт переходного процесса с помощью интеграла Дюамеля
- •3. Пример выполнения курсовой работы
- •3.1Постановка задачи в курсовой работы
- •Пример выполнения задачи № 1
- •Пример выполнения задачи № 1 в программеMathCad
- •Пример моделирование задачи № 1 в программе matlab и simulink
- •3.3 Пример выполнения задачи №2.
- •Пример выполнения задачи № 2 в программеMathCad
- •Пример моделирование задачи № 2 в программеMatlab и simulink
- •3.3 Пример выполнения задачи №3
- •Пример выполнения задачи № 3 в программеMathCad
- •Пример моделирование задачи № 3 в программеMatlab и simulink
- •3.3 Пример выполнения задачи №4.
- •Пример выполнения задачи № 4 в программеMathCad
- •Пример моделирование задачи № 4 в программеMatlab и simulink
- •3.3 Пример выполнения задачи №5.
- •Пример выполнения задачи № 5 в программеMathCad
- •Пример моделирование задачи № 5 в программеMatlab и simulink
- •3.3 Пример выполнения задачи №6
- •Пример выполнения задачи № 6 в программеMathCad
- •Пример моделирование задачи № 6 в программеMatlab и simulink
- •3.3 Пример выполнения задачи №7
- •Пример выполнения задачи № 7 в программеMathCad
- •Пример моделирование задачи № 7 в программеMatlab и simulink
- •3.4 Пример выполнения задачи №8
- •1 Рассчитать переходной процесс для ток iA(t), в полученной однофазной классическим методом
- •3.3 Пример выполнения задачи №9
- •Пример моделирование задачи № 9 в программеMatlab и simulink
- •Пример моделирование задачи № 9 в программеMatlab и simulink
- •Библиографический список
- •Рассоха Дмитрий Павлович
4.3 Фильтр напряжения обратной последовательности (фноп)
Наиболее распространенная схема ФНОП состоит из активных сопротивлений и конденсаторов, соединенных в разомкнутую мостовую схему (рисунок 4.4).
При изменении подключения двух фаз фильтр преобразуется в фильтр напряжения прямой последовательности.
Рассмотрим работу фильтра при отключенной нагрузке. При подключении нагрузки изменяется только абсолютная величина выходного напряжения, основные соотношения, характеризующие его работу, остаются неизменными.
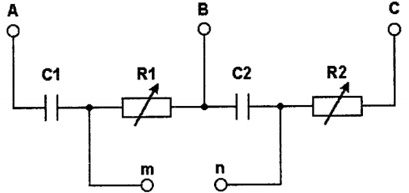
Рис. 4.4
Напряжение нулевой последовательности во всех трех фазах имеет одинаковое значение, поэтому входные зажимы под действием составляющей нулевой последовательности находятся под одним потенциалом. Напряжение на выходе ФНОП, определяемое разностью потенциалов на входных зажимах, будет равно нулю. Под действием системы напряжений прямой и обратной последовательности по элементам фильтра протекает ток.
Сопротивления плеч фильтра выбираются таким образом, чтобы при подведении к нему напряжений прямой последовательности напряжение между точками m и п было равно нулю. Для выполнения этого условия напряжение на резисторе R1 должно компенсировать напряжение на конденсаторе С2:
 . (4.4)
. (4.4)
Это обеспечивается подбором элементов фильтра. Напряжения на активных и емкостных сопротивлениях связаны отношениями:
-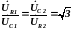 (4.5)
(4.5)
При выполнении отношений (4.5) векторы напряжений образуют два прямоугольных треугольника с углами 30° и 60°.
Диаграммы напряжений на элементах фильтра при подаче напряжений прямой и обратной последовательности приведены на рисунках 4.5, 4.6.
При подаче напряжения прямой последовательности частотой 50 Гц потенциалы точек тип равны, напряжение на выходе фильтра равно нулю. Если частота отличается от нормальной, на выходе фильтра появляется напряжение небаланса.
При подаче напряжения обратной последовательности между зажимами m и n появляется прямо пропорциональное ему напряжение:
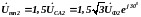 (4.6)
(4.6)
где
 — напряжение
на выходе фильтра при подаче напряжения
обратной последовательности;
— напряжение
на выходе фильтра при подаче напряжения
обратной последовательности;
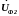 —
составляющая
обратной последовательности фазного
напряжения.
—
составляющая
обратной последовательности фазного
напряжения.
Р |
|
Р |
Сопротивление нагрузки фильтра подбирается таким образом, чтобы отдаваемая фильтром мощность была максимальной. Условие отдачи максимальной мощности — равные по величине и противоположные по знаку реактивные сопротивления фильтра и нагрузки.
4.4 Фильтры тока обратной последовательности (фтоп)
Эти фильтры более разнообразны, чем ФНОП. Один из возможных фильтров приведен на рисунке 4.7.
Рис. 4.7 |
Фильтр состоит из трехобмоточного трансформатора с воздушным зазором ТА1, регулируемого активного сопротивления R и двухобмоточного вспомогательного трансформатора ТА2.
Трансформатор ТА1 имеет две первичные и одну вторичную обмотку. Первичные обмотки включены в токовые цепи фаз А и В с противоположной полярностью.
Создаваемый
ими магнитный поток пропорционален
разности токов IА
и IB.
Этот поток индуктирует во вторичной
обмотке ТА1 ЭДСГ
отстающую от индуцирующего ее потока
и тока
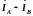 на 90°:
на 90°:
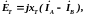 (4.7)
(4.7)
где
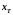 =
=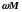 —
реактивное сопротивление, обусловленное
взаимоиндукцией обмоток трансреактора.
—
реактивное сопротивление, обусловленное
взаимоиндукцией обмоток трансреактора.
Наличие воздушного зазора в магнитопроводе трансреактора обеспечивает линейную зависимость величины ЭДС от тока . Величина сопротивления самоиндукции и активного сопротивления R связаны отношением:
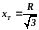 (4.8)
(4.8)
что является необходимым условием для исключения влияния токов прямой последовательности на выходное напряжение фильтра.
Ток IС протекает через резистор R. В результате этого на его зажимах появляется напряжение, определяемое выражением:
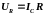 . (4.9)
. (4.9)
Выходной контур фильтра mn образуется вторичной обмоткой трансреактора и сопротивлением R. Напряжение на разомкнутых зажимах mn равно сумме ЭДС взаимоиндукции и напряжения UR:
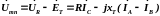 . (4.10)
. (4.10)
При подаче токов нулевой последовательности магнитные потоки, образуемые в трансреакторе ТА1 токами фаз А и В, взаимно уничтожаются благодаря принятой схеме включения трансреактора на разность токов. Ток фазы С, проходящий через активное сопротивление, компенсируется с помощью трансформатора ТА2, включенного в нулевой провод на ток 3I0. Коэффициент трансформации ТА2 равен 1/3, поэтому вторичный ток его равен току I0. Следовательно, токи нулевой последовательности взаимно компенсируются.
Токи прямой последовательности IА1,IВ1, протекающие через трансреактор ТА1, создают ЭДС:
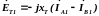 . (4.11)
. (4.11)
Так как ЭДС на выходе ТА1 отстает от разности токов на 90°, ЭДС и напряжение на сопротивлении при выполнении условия а3=1 взаимно компенсируются:
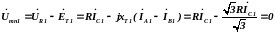 . (4.12)
. (4.12)
При подаче тока обратной последовательности векторы ЭДС и напряжения совпадают по фазе, и их суммарная величина составляет:
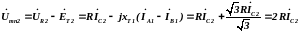 (4.13)
(4.13)
Таким образом, рассматриваемая схема является фильтром токов обратной последовательности.
Если к выходным зажимам в качестве нагрузки подключить токовое реле, ток в нем составит:
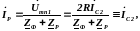 (4.14)
(4.14)
где ZФ — сопротивление фильтра, измеренное со стороны выходных зажимов mn при разомкнутой цепи на входе фильтра;
ZP— сопротивление реле.
Ток небаланса возникает из-за неточного подбора элементов фильтра или отклонения частоты в сети от номинальной.
Векторные диаграммы фильтра при подаче токов прямой и обратной последовательности приведены на рисунке 4.8 а.б.
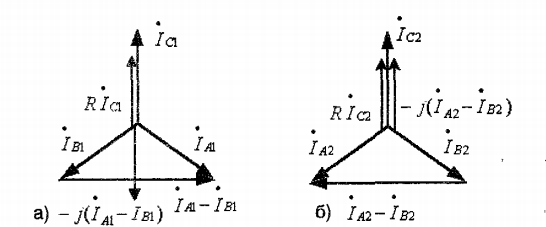
Рис. 4.8
Другие схемы ФТОП приведены при рассмотрении отдельных реле и комплектов защит.
Если поменять местами две фазы токов, получим фильтр токов прямой последовательности (ФТПП). В чистом виде такие фильтры практически не используются.
В некоторых случаях применяются фильтры, в которых отношение (4.8) искусственно нарушено на дозированную величину. Это позволяет получить комбинированный фильтр, напряжение на выходе которого пропорционально некоторому отношению токов прямой и обратной последовательности. Пример такого фильтра — орган манипуляции дифференциально-фазной защиты, описание которого приведено в соответствующем разделе настоящего пособия.

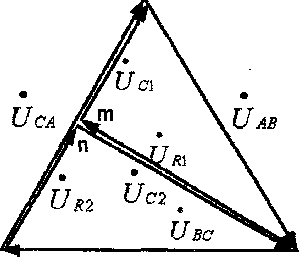 ис.
4.5
ис.
4.5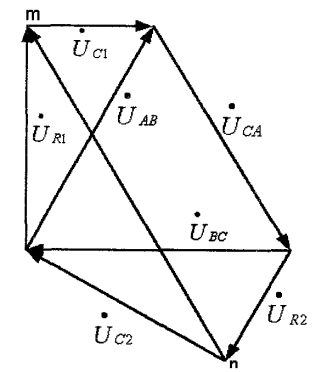 ис.
4.6
ис.
4.6