2.6.5 Метод переменных состояния

2.6.5.1 . Общие понятия и определения

Анализ переходных процессов в линейных цепях классическим или операторным методом сводился к решению дифференциального уравнения:

(6.5.1)

где x(t) – это ток или напряжение в элементе или ветви;

n – порядок цепи после коммутации, который определяется количеством емкостей и индуктивностей;

F(t) – это источники электрической энергии, в цепи после коммутации.

Классический и операторный методы помогают найти точное решение дифференциального уравнения (6.5.1), если порядок цепи не выше второго, если выше второго – корни характеристического уравнения определяются приближенными методами.

Основной недостаток классического метода – это нахождение зависимых начальных условий, а основной недостаток операторного – получение операторного изображения искомой величины и переход от изображения к оригиналу, если корни характеристического уравнения – кратные.

Кроме того, эти методы практически не поддаются автоматизации на ПЭВМ. Поэтому в 50-х годах ХХ века был предложен метод переменных состояний, с помощью которого рассчитываются переходные процессы в цепях путем решения системы дифференциальных уравнений первого порядка.

Таким образом, методом переменных состояния назовем анализ схемы, основанный на решении системы дифференциальных уравнений первого порядка (уравнений состояния), записанных в форме Коши.

Введением переменных x₁=х; 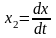; ; 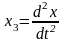… ; 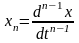уравнение (6.5.1) сводится к эквивалентной системе дифференциальных уравнений первого порядка:

(6.5.2)

В системе (6.5.2) переменная х и ее производные называются переменными состояния.

Как известно, переходный процесс в любой схеме определяется параметрами R, L, С, М и функциями источников e(t) и j(t), а также независимыми начальными условиями при t=0: токами в индуктивных элементах i_L(0) и напряжениями на емкостных элементах u_C(0), которые должны быть известны или рассчитаны. Через i_L(0) и u_C(0) выражаются искомые величины во время переходного процесса. Они же определяют энергетическое состояние схемы. Поэтому в качестве переменных состояния целесообразно выбирать токи i_L(t) и напряжения u_C(t). Источники, включенные в схему, можно назвать входными величинами [F₁(t), ..., F_m(t)], искомые величины – выходными величинами [y₁(t) , ... , y_l(t)]. Для цепи с п независимыми токами i_L(t) и напряжениями u_C(t) должны быть заданы еще п независимых начальных условий.

Сокращенно дифференциальные уравнения состояния запишем в матричной форме:

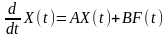, (6.5.3)

где Х – матрица-столбец (размера пх1) переменных состояния (вектор переменных состояния); F – матрица-столбец (размера mх1) э.д.с. и токов источников (внешних возмущений); А – квадратная матрица порядка n (основная); В – матрица размера пхт (матрица связи). Элементы этих матриц определяются топологией и параметрами цепи.

Для выходных величин (если определяются не токи в индуктивных элементах и напряжения на емкостных элементах) в матричной форме система алгебраических уравнений имеет вид

Y(t) = MX(t) + NF(t), (6.5.4)

где Y– матрица-столбец (размера l х 1); М – матрица связи (размера l х n); N – матрица связи (размера l х m).

Элементы матриц зависят от топологии и параметров схемы. Для уравнений состояния разработаны и машинные алгоритмы формирования на основе топологии и значений параметров.