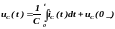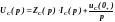2.6.4 Операторный метод

Одним из способов решения подобной системы уравнений является операторный метод.

Сущность операторного метода заключается в том, что функции времени f(t) , которые называется оригиналами, заменяются их операторными изображениями F(р). Соответствие между оригиналом и изображением устанавливают при помощи функционального преобразования, которое выбирается таким образом, чтобы операции дифференцирования и интегрирования оригиналов заменялись алгебраическими операциями над их изображениями. В этом случае интегро-дифференциальные уравнения для оригиналов переходят в алгебраические уравнения для их изображений, то есть осуществляется алгебраизация исходной системы дифференциальных уравнений. В результате решения алгебраической системы уравнений в операторной форме определяются изображения искомых функций, а затем по этим изображениям - соответствующие им оригиналы, то есть Функции времени.

Связь между оригиналом f(t) и его изображением F(р) устанавливается с помощью интегрального преобразования Лапласа

,

где - комплексное число, которое называется оператором.

Каждый оригинал имеет единственное изображение. В свою очередь, оригинал однозначно определяется по своему изображению.

Используя функциональное преобразование Лапласа, мы заменяем операции дифференцирования и интегрирования функций-оригиналов алгебраическими операциями умножения и деления на оператор р изображений этих функций.

При составлении уравнений цепи в операторной форме автоматически учитываются все физические начальные условия - значения токов в катушках и напряжений на зажимах конденсаторов при t=0_-. Отпадает необходимость определения зависимых начальных условий и постоянных интегрирования.

Решение системы алгебраических уравнений для операторного изображения имеет в общем случае следующий вид:

,

где a_m…a₀,b_n..b₀ вещественные числа, F₁(p) и F₂(p) - степенные многочлены, которые не имеют общих корней.

Переход от изображения F(p) к оригиналу f(t) осуществляется по теореме разложения. Из условия F₂(p) определяются корни р_к, количество которых может быть больше числа корней характеристического уравнения. Дополнительные корни появляются за счёт изображения внешних источников.

В зависимости от вида корней выбирается соответствующая форма записи теоремы разложения. Возможны следующие варианты:

• корни простые

;

- корни сопряжённые комплексные ( )

- корни равные кратности m

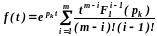
Изображения простейших функций

Теорема разложения в сочетании с другими свойствами преобразования Лапласа даёт возможность составить таблицы оригиналов и изображении, которые облегчают и ускоряют расчёты переходных процессов операторным методом. В табл6.4.1 приведены соотношения между оригиналами и изображениями, наиболее часто встречающиеся в расчетной практике.

Таблица 6.4.1

Оригинал f(t)	Изображение F(p)
A
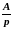
A
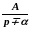
Sin t
Cos t

Законы Кирхгофа в операторной форме. Операторные схемы

Первый закон Кирхгофа может быть записан в операторной форме как

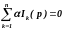
Соответственно второй закон Кирхгофа в операторной форме выглядит следующим образом

При составлении уравнений по законам Кирхгофа в операторной форме необходимо задаться положительными направлениями всех токов и соблюдать все правила знаков, установленные ранее при записи уравнений Кирхгофа для функций времени.

Нетрудно увидеть, что структуры уравнений, составленных по законам Кирхгофа в операторной и комплексной формах, тождественны.

Поэтому все способы расчёта цепей в переходном режиме операторным методом аналогичны способам расчёта цепей в установившемся режиме комплексным методом.

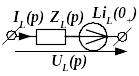
При расчете электрических цепей для отдельных элементов цепи имеют место вполне определенные соотношения между изображениями токов и напряжений. На основании этих соотношений для каждого элемента цепи можно дать операторную схему замещения, и всю цепь заменить эквивалентной операторной схемой. В табл6.4.2 приведены соотношения между оригиналами и изображениями для элементов линейных электрических цепей и соответствующие им операторные схемы.

Таблица 6.4.2

Элемент схемы	Уравнение в дифференциальной форме	Уравнения в операторной форме	Операторная схема замещения
j(t)	j(t)	J(p)	J(p)
e(t)	e(t)	E(p)	E(p)
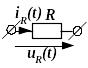
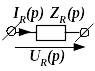
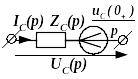
	uR(t)=RiR(t)	UR(p)=ZR(p)IR(p)

Рекомендуемый порядок расчёта переходных процессов операторным методом

Переходный процесс в цепи с сосредоточенными параметрами можно рассчитать операторным методом по следующему алгоритму:

- расчетом цепи докоммутационной конфигурации определяются независимые начальные условия i_L (0_) и u_C (0_);

- составляется операторная схема замещения, соответствующая исходной цепи послекоммутационной конфигурации согласно табл.6.4.2;

- операторная схема рассчитывается относительно изображения искомой функции методами, аналогичными методам расчета цепей с синусоидальными источниками в установившемся режиме;

- осуществляется переход от полученного изображения к оригиналу, то есть к искомой функции времени. При нахождении функции-оригинала используют, как правило, теорему разложения.